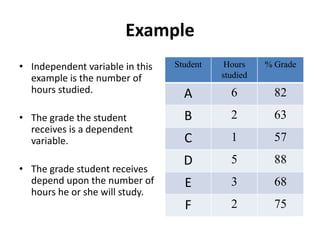
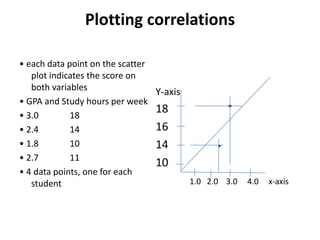
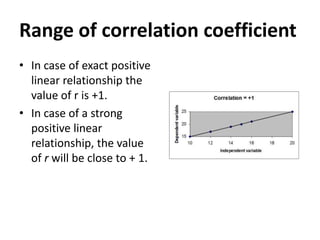
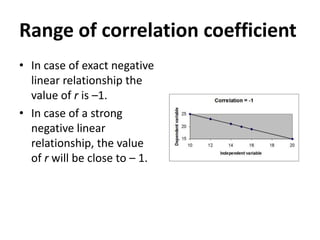
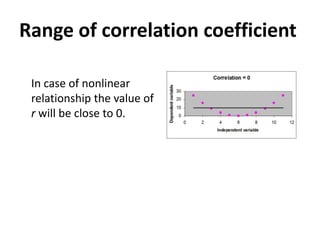
This document provides an overview of correlational research and inferential statistics. It defines correlation as measuring the relationship between two variables, and explains that correlational research allows determining if variables are related but not if there is a causal relationship. Key aspects covered include independent and dependent variables, the Pearson correlation coefficient for measuring strength and direction of relationships, and types of correlations. Scatter plots and examples are used to illustrate concepts. Hypothesis testing and different sampling methods are also summarized.

1. Correlation
Research
&
Inferential
by
Statistics A. Askar
Atheer L. Khamoo & Wissam

2. Table of Content
•
•
•
•
•
•
•
Definition
Purpose
Independent and dependent variables
Scatter plot
Correlation coefficient
Range of correlational coefficient
Types of correlational study

3. Correlational research
A correlational is the measurement of the
relationship between two variables.
Correlation is a statistical technique that can
show whether and how strongly pairs of
variables are related.

4. The Goal of Correlational Research
The goal of correlational research is to find out
whether one or more variables can predict other
variables.
Correlational research allows us to find out
what variables may be related. However, the fact
that two things are related or correlated
does not mean there is a causal relationship. It is
important to make a distinction between
correlation and causation. Two things can be
correlated without there being a causal relationship

5. Independent and Dependent Variables
• Independent variable: is a variable that can be
controlled or manipulated.
• Dependent variable: is a variable that cannot
be controlled or manipulated. Its values are
predicted from the independent variable

6. Example
• Independent variable in this
example is the number of
hours studied.
• The grade the student
receives is a dependent
variable.
• The grade student receives
depend upon the number of
hours he or she will study.
Student
Hours
studied
% Grade
A
6
82
B
2
63
C
1
57
D
5
88
E
3
68
F
2
75

7. Definition of 'Pearson Coefficient'
• A type of correlation coefficient that
represents the relationship between
two variables that are measured on the
same interval or ratio scale.

8. Pearson Correlation Coefficient
• A number between –1.0 and +1.0
describes the relationship between 2 variables:
•
•
•
•
•
direction (+ positive or – negative)
strength (from 0 to ±1)
r = +1.0 a very strong positive relationship
r = –1.0 a very strong negative relationship
r = 0 there is no relationship

9. Types of correlations
• A positive relationship exists when both
variables increase or decrease at the same
time. (Weight and height).
• A negative relationship exist when one
variable increases and the other variable
decreases or vice versa. (Strength and age).
• No Correlation indicates no relationship
between the two variables. A correlation
coefficient of 0 indicates no correlation

10. Scatter Plot
• The independent and dependent can be
plotted on a graph called a scatter plot.
• By convention, the independent variable is
plotted on the horizontal x-axis.
• The dependent variable is plotted on the
vertical y-axis.

11. Plotting correlations
• each data point on the scatter
plot indicates the score on
both variables
Y-axis
• GPA and Study hours per week
18
• 3.0
18
16
• 2.4
14
• 1.8
10
14
• 2.7
11
10
• 4 data points, one for each
1.0 2.0 3.0
student
4.0
x-axis

12. Range of correlation coefficient
• In case of exact positive
linear relationship the
value of r is +1.
• In case of a strong
positive linear
relationship, the value
of r will be close to + 1.

13. Range of correlation coefficient
• In case of exact negative
linear relationship the
value of r is –1.
• In case of a strong
negative linear
relationship, the value
of r will be close to – 1.

14. Range of correlation coefficient
In case of nonlinear
relationship the value of
r will be close to 0.

15. Types of Correlational Studies:
1. The Survey Method
• Survey and questionnaires are one of the
most common methods used in educational
research. In this method, a random sample of
participants completes a survey, test, or
questionnaire that relates to the variables of
interest.
• Random sampling is a vital part of ensuring
the generalizability of the survey results.

16. Advantages of the survey method
• It’s fast, cheap, and easy. Researchers can
collect large amount of data in a relatively
short amount of time.
• More flexible than some other methods

17. Disadvantages of the Survey Method:
• Can be affected by an unrepresentative
sample or poor survey questions.
• Participants can affect the outcome. Some
participants try to please the researcher, lie to
make themselves look better, or have
mistaken memories.

18. 2. Archival Research
• Archival research is the study of existing data.
The existing data is collected to answer research
questions. Existing data sources may include
statistical records, survey archives, and written
records.

19. Advantages of Archival Research:
• The experimenter cannot introduce changes in
participant behavior.
• Enormous amounts of data provide a better
view of trends, relationships, and outcomes.
• Often less expensive than other study
methods. Researchers can often access data
through free archives or records databases.

20. Disadvantages of Archival Research:
• The researchers have not control over how
data was collected.
• Important date may be missing from the
records.

22. Inferential Statistics
•
One use of statistics is to be able to make inferences or
judgments about a larger population based on the data
collected from a small sample drawn from the population
•
Statistical inference is a procedure by means of which you
estimate parameters (characteristics of population) from
statistics (characteristics of samples).
Population
Sample

23. Rationale of sampling
• The inductive method involves making
observations and then drawing conclusions
from these observation.
• Samples must be representative if you are to
be able to generalize with reasonable
confidence from the sample to the population.
• An unrepresentative sample is termed a
biased sample

24. Steps in sampling
1. Probability sampling
It involves sample selection in which the
elements are drown by chance procedures.
2. Nonprobability sampling
It includes methods of selection in which
elements are not chosen by chance
procedure.

25. The types of probability sampling
1. Simple random sampling
2. Stratified sampling
3. Cluster sampling
4. Systematic sampling

26. 1. Simple random sampling
It comprise the following steps:
1. Define the population
2. List all members of the population
3. Select the sample by employing a procedure
where sheer chance determines which
members on the list are drawn for the sample.

27. 2. Stratified sampling
Population consists of a number of subgroups,
or strata, that may differ in the characteristics
being studied.

28. 3. Cluster sampling
• With cluster sampling, the researcher divides
the population into separate groups, called
clusters. Then, a simple random sample of
clusters is selected from the population.

29. 4. Systematic sampling
A common way of selecting members for a sample
population using systematic sampling is simply to
divide the total number of units in the general
population by the desired number of units for the
sample population.
For example, if you wanted to select a random
group of 1,000 people from a population of 50,000
using systematic sampling, you would simply select
every 50th person, since 50,000/1,000 = 50.

30. Non probability sampling
1- Convenience sampling, It is a sampling method in which
units are selected based on easy access/availability. which is
regarded as the weakest of all sampling procedures, involves
using available cases for study.
2- Purposive sampling a type of nonprobability sampling in
which the researcher consciously selects specific elements or
subjects for inclusion in a study in order to ensure that the
elements will have certain characteristics relevant to the
study.
3- Quota Sampling involves selecting typical cases from
diverse strata of a population. The quotas are based on known
characteristics ( age, gender, social class, etc.,) of the
population to which you wish to generalize.

31. Random Assignment
• When the primary goal of a study is to
compares the outcomes of two treatments
with the same dependent variable, random
assignments is used. Here a chance procedure
such as a table of random numbers is used to
divide the available subjects into groups.
• Then a chance procedure such as tossing a
coin is use to decide which group gets which
treatments.

32. The size of the sample
How large should a sample be?
• A larger sample is more likely to be a good
representative of the population than a smaller sample.
However, the most important characteristic of a sample
is its representativeness, not its size.
• A random sample of 200 is better than a random sample
of 100, but a random sample of 100 is better than biased
sample of 2500000.

33. The concept of sampling error
• The researcher has observed only a sample
and not the entire population.
• Sampling error is “the difference between a
population parameter and a sample statistic”.

34. Hypothesis Testing
A statistical hypothesis is an assumption about
a population parameter. This assumption may or
may not be true. Hypothesis testing refers to
the formal procedures used by statisticians to
accept or reject statistical hypotheses.

35. There are two types of statistical hypotheses.
• Null hypothesis. The null hypothesis, denoted by
H0, is usually the hypothesis that sample
observations result purely from chance.
The null always says there is no relationship or
difference
H0 (null) is that mean1=mean2, meaning the
mean scores are equal OR the difference
between the mean scores is zero .

36. • Alternative hypothesis ( Hi )
• It means, there is a difference between two
groups or there is a statistically significant
difference of population.
• Types of alternative hypothesis.
- Non-directional
- Directional

37. Example:
Ho :- There is no statistically significant differs between teachers
based on their gender in their attitude towards first language used of
EFL classroom.
Hi :- There is a statistically significant differs between teachers based
on their gender in their attitude towards first language used of EFL
classroom.
_ Non-directional; because they didn’t mention which one use
more/less according to ( male/female).
_ Directional; female teachers have more positive attitude than male
towards use of first language in EFL in classroom.

38. Two types of errors can result from a hypothesis test.
• Type I error. A Type I error occurs when the
researcher rejects a null hypothesis when it is
true. This probability is also called alpha, and is
often denoted by α.
• Type II error. A Type II error occurs when the
researcher fails to reject a null hypothesis that is
false. The probability of committing a Type II
error is called Beta, and is often denoted by β.
• Type I _ reject true null ; Type II _ accept a false

39. State level of significance
• Level of significance = risk of rejecting a TRUE
Hypothesis
• Determine the probability of getting the sample
results by chance if the null is true.
• Small probability (p<.05) means reject null;
there is a significant difference.
• Large probability ( p>.05) means do not reject;
there is no significant difference.

40. Degrees of Freedom
• The number of degrees of freedom ( df ) is
the number of observations free to vary
around a constant parameter. To illustrate the
general concept of degrees of freedom.

41. References
Anderson, A. (1990). Fundamentals of educational research. USA: The falmer.
Ary, D. & et al., (2006). Introduction to research in education .(7th ed.). USA: Thomson.
Best, J. W. & Kahn, J. V. (2006). Research in education.(10th ed.) : USA: Pearson.
Cherry, K. (2012). Correlational Studies . December 12, 2012 retrieved from
http://psychology.about.com/od/researchmethods/a/correlational.htm
Cherry, K. (2012). Introduction to Research Methods. December 12, 2012 retrieved from
http://psychology.about.com/od/researchmethods/ss/expdesintro_5.htm