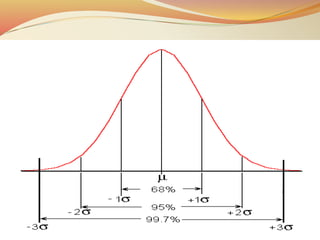
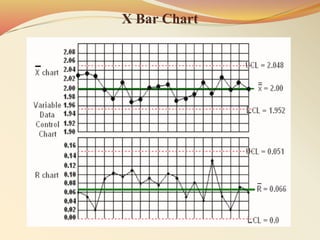
Control charts, founded by Walter A. Shewhart in 1924, are statistical tools for quality control used to monitor process performance over time. They display data chronologically to assess stability, understand process variations, and determine capabilities through upper and lower control limits. While control charts offer advantages like diagnosing process improvements and identifying variations, they also have drawbacks such as lack of explanations for variations and challenges with complex data.

1. CONTROL CHARTS

2. Founder of Control Charts in 1924
Walter A. Shewhart

3. 1. Statistical tool used in quality control.
2. Chronological recording of data.
3. Presented in a graphical form.
4. How a process is performing over time.
5. To analyze and understand process variables.
6. Determine process capabilities.
7. Difference between target and actual performance.
8. Upper and lower limits helps the process should operate.

4. Definition
A graphical technique for determining whether a
process is or is not in a state of statistical control the
extent of variation of the output of the process does
not exceed that which is expected based on the
natural statistical variability of the process.

5. Salient Features
 Points representing a statistic - a mean, range, proportion of
measurements in samples are taken at different time.
 Any statistical data can be calculated by using samples.
 Upper + lower control limit = "natural process limits“.
 Control charts focus on stability by statistical fluctuations.

6. Where are Control Charts used?
 Project Works
 Cyclical activities - Manufacturing / Production
 Scientific Space crafts
 Logistics
 Mathematics and Statistics
 Industrial aspects
 Research and Development
 Sample & Data collections ( Demography)

7. P D C A
PLAN
DO
CHECK
ACT

8. Act – Apply the change or
abandon it, or run
through the cycle again
under different
conditions.
Check – The results
of your action. What
did you learn?
Do – Implement a
change or test a small
scale
Plan - Aimed at
improvement –
Collect Data –
Establish timeframe.

9. Advantages
 Sign whether is in control or out of control
 Particular level of quality.
 Investigate on unusual variations.
 Explore on cause & effect relationship.
 Warning limits - before the process is out of control.
 Diagnosing on process improvements.
 No knowledge about the underlying distribution of the variable.
 Identify the presence of an assignable cause of variation.

10. Drawbacks
 Insufficient explanation on "WHY” it is out of control.
 Difficult to identify a subgroup
 Greater risk without experts.
 Non-verification on adverse event.
 Non accuracy on forecasting.
 Multivariate, seasonal data – inflexible.
 Inadaptable to complexities.

11. Maximization Concept
 Improves product quality
 Raise in productivity
 Restructure process
 Expansion
 Diversification
 Reduce wastages
 Enhance customer service

14. Normal Distribution

17. X Bar Chart

18. Attribute Chart

20.  X-bar chart - In this chart the sample means are plotted in order to
control the mean value of a variable (e.g., size of piston rings, strength of
materials, etc.).
 R chart - In this chart, the sample ranges are plotted in order to control
the variability of a variable.
 S chart - In this chart, the sample standard deviations are plotted in order
to control the variability of a variable.
 C chart - In this chart we assumes that defects of the quality attribute are
rare, and the control limits in this chart are computed based on the Poisson
Distribution (distribution of rare events).

21.  U chart - In this chart we plot the rate of defectives, this chart does
not require a constant number of units, and it can be used, for example,
when the batches (samples) are of different sizes.
 Np chart - The control limits in this chart are not based on the
distribution of rare events, but rather on the binomial distribution. We
may use this chart to control the number of units produced with minor
flaws.
 P chart - This chart is most applicable to situations where the
occurrence of defectives is not rare (e.g., we expect the percent of
defectives to be more than 5% of the total number of units produced).

22. Process Capability
 Process capability expressed as a ratio of parts or items
produced by the current process that fall within user-specified
limits (e.g., engineering tolerances).
 For example, the so-called Cp index is computed as:
Cp = (USL-LSL)/(6*sigma)

23. THANK YOU