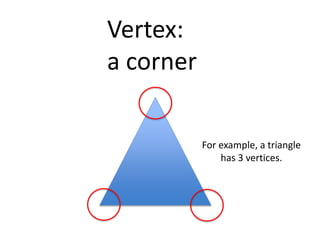
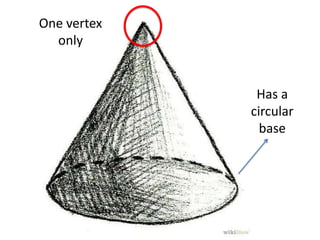
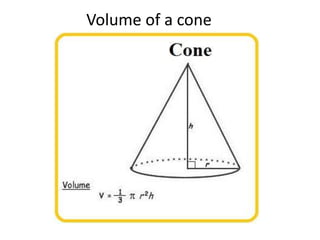
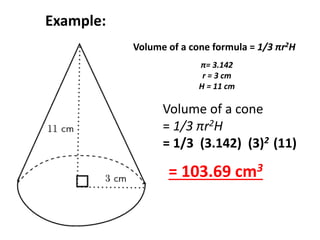
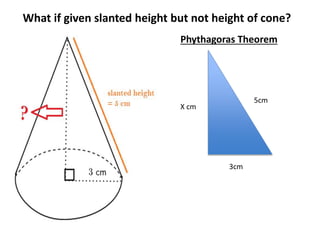
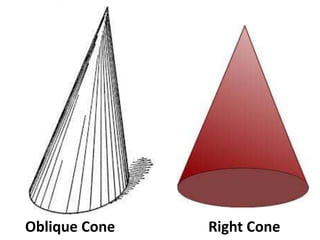
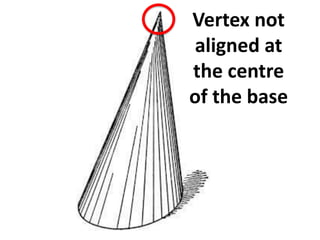
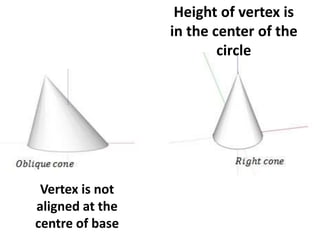
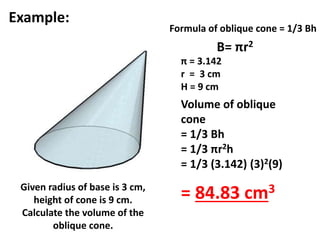
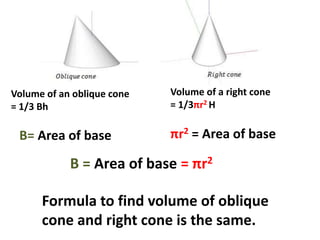
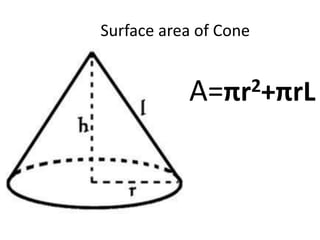
A cone is a 3D shape with a circular base and a single vertex. To calculate the volume of a cone, use the formula V=1/3πr^2h. This formula can be used for both right and oblique cones, where the volume equals 1/3 times the area of the base times the height. The area of the base is πr^2 for both types of cones.

1. CONE

2. CONE DEFINITION:
-a 3-dimensional solid object
that has :
a) circular base,
b) one vertex.

3. Vertex:
a corner
For example, a triangle
has 3 vertices.

4. How do we
determine which is
a cone?

5. Has a
circular
base
One vertex
only

6. Volume of a cone

7. Example:
Volume of a cone formula = 1/3 πr2H
π= 3.142
r = 3 cm
H = 11 cm
Volume of a cone
= 1/3 πr2H
= 1/3 (3.142) (3)2 (11)
= 103.69 cm3

8. What if given slanted height but not height of cone?
Phythagoras Theorem
5cm
3cm
X cm

9. 5cm
3cm
X cm
√( X2 + 32) = 52
X2 = 52 – 32
X2 = 16
X=√16
X= 4cm

10. Oblique Cone?

11. Definition :
-A cone with an vertex
that is not aligned above
the centre of the base.

12. Oblique Cone Right Cone

13. Vertex not
aligned at
the centre
of the base

14. Vertex is not
aligned at the
centre of base
Height of vertex is
in the center of the
circle

15. Formula
Volume of an oblique cone
= 1/3 (area of base)(cone
height)
= 1/3 Bh
B= πr2

16. Formula of oblique cone = 1/3 Bh
B= πr2
π = 3.142
r = 3 cm
H = 9 cm
Volume of oblique
cone
= 1/3 Bh
= 1/3 πr2h
= 1/3 (3.142) (3)2(9)
= 84.83 cm3
Example:
Given radius of base is 3 cm,
height of cone is 9 cm.
Calculate the volume of the
oblique cone.

17. Conclusion

18. Volume of an oblique cone
= 1/3 Bh
Volume of a right cone
= 1/3πr2 H
B= Area of base πr2 = Area of base
B = Area of base = πr2
Formula to find volume of oblique
cone and right cone is the same.

19. Surface area of Cone
A=πr2+πrL

20. The End