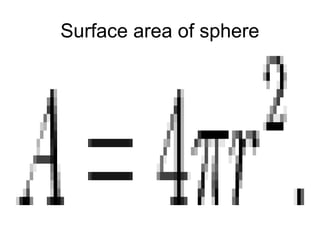
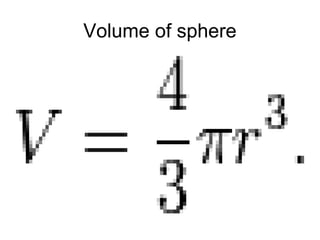The document discusses the key properties and formulas for calculating the volume and surface area of different geometric shapes including pyramids, cones, and spheres. It outlines that pyramids can have different polygon bases and be right or oblique. The volume of a pyramid is calculated using the base area and height, while surface area considers the total area of all faces and the base. For cones, volume is 1/3 the base area times height, and surface area includes the curved area and base. Sphere volume and surface area formulas are also presented.

1. Volume and Surface area
Cone
Pyramid
Sphere

2. Pyramid
• A pyramid is a polygonal base with a
vertex
• All the faces are triangle which meet at the
vertex
• There are several types of pyramid




Triangle based pyramid- Tetrahedron
Quadrilateral based pyramid
Pentagon based pyramid
Hexagon based pyramid

3. • The pyramid where vertex is directly
above the centre of the base is known as
right pyramid and the pyramid that doesn’t
have vertex directly above the vertex is
called Oblique Pyramids.

4. • Perpendicular of pyramid (height) :
distance from the vertex to the base of the
pyramid
• Slant height: distance from the vertex to
the mid point of an edge of the base

5. Volume of Pyramid

6. Net of Pyramid

7. Surface area pf Pyramid
•
•
•
Surface area: : The number of
square units that will exactly cover
the surface of a pyramid.
In the case of a right pyramid, the
side faces are all the same, so we
can simply find the area of one
and multiply by the number of
faces. Once we add the area of
the base, we have the total
surface area.
Surface area of pyramid= total
area of all its faces+ base area.
Area of the
base
Area of the four
faces 4 times
=TOTAL

8. Cone
•A cone tapers smoothly from a flat base (usually
circular) to a point called the apex or vertex.
•The axis of a cone is the straight line passing through
the apex
• Cones are assumed to be right circular,
where right means that the axis passes through the
centre of the base circular means that the base is a circle

9. Volume of cone
• The volume of any conic solid is one third
of the product of the area of the base and
the height (the perpendicular distance
from the base to the apex).
• 1/3*base area* height

10. Surface area of cone
• By folding the quadrant a cone will be
obtained
• The curved surface area of the cone is the
area of quadrant
• Curved Surface Area = πrl

11. Total surface area
• Area of quadrant or curved surface area+
base area

12. Sphere

13. Volume of sphere

14. Surface area of sphere