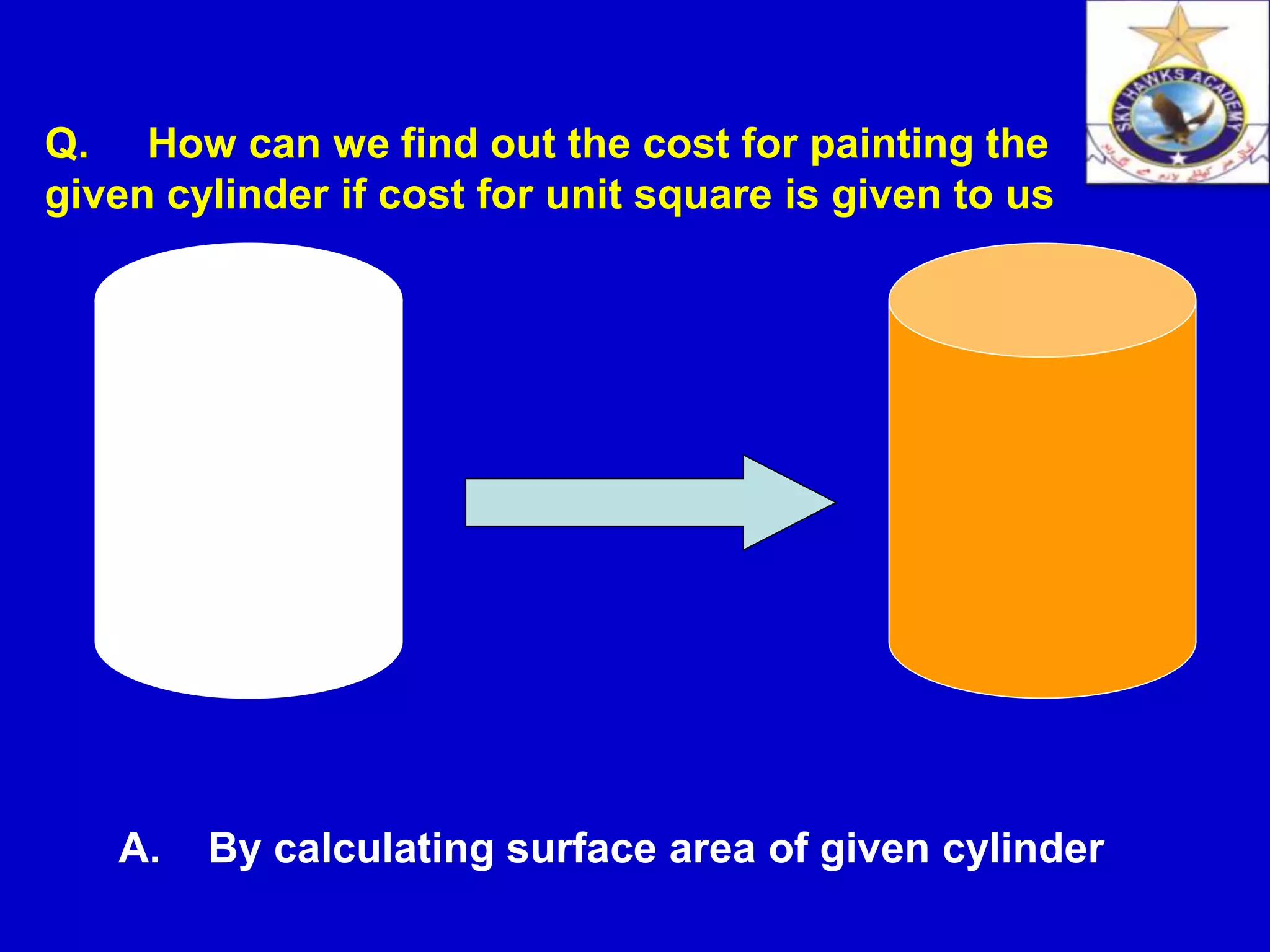
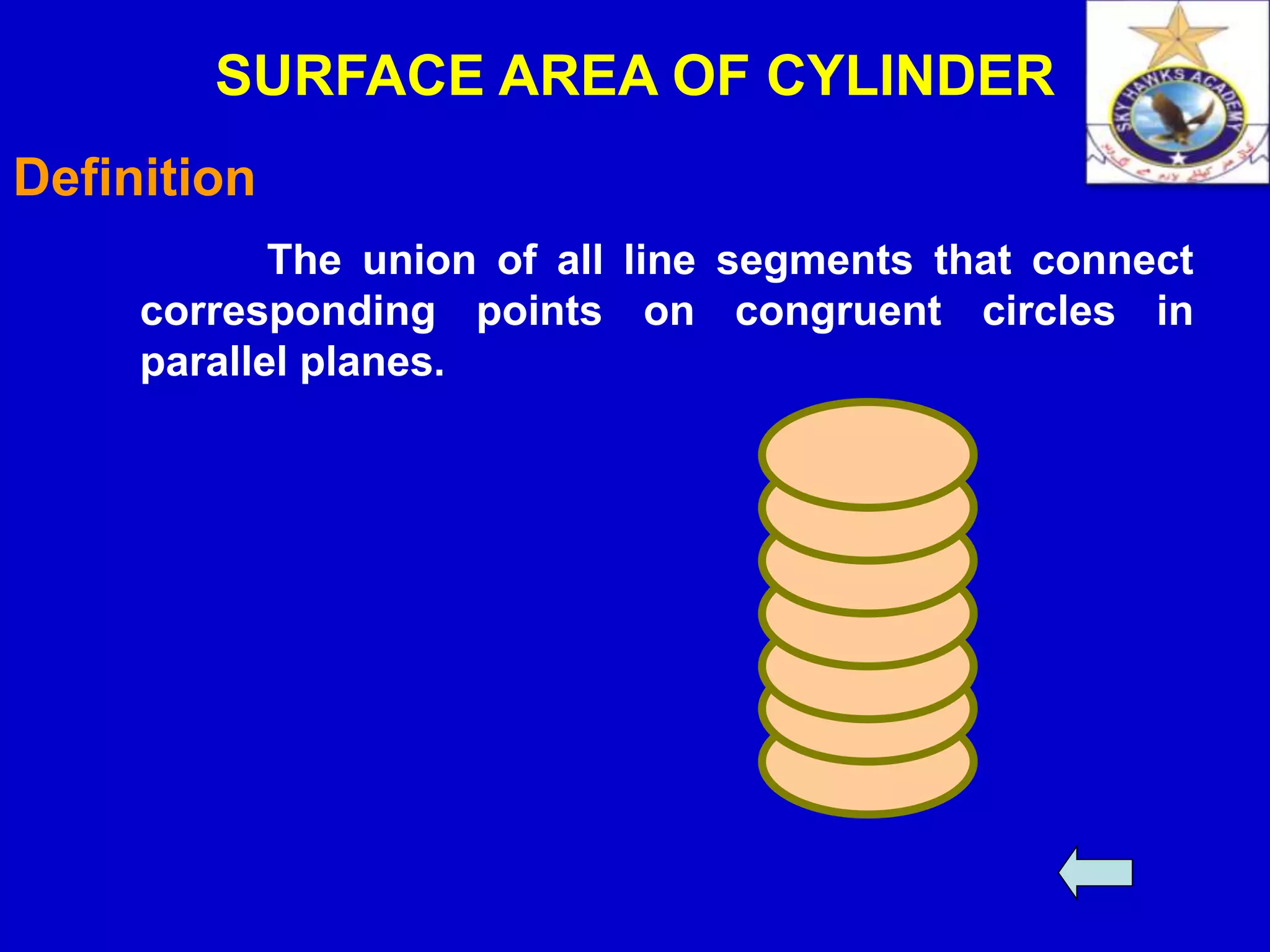
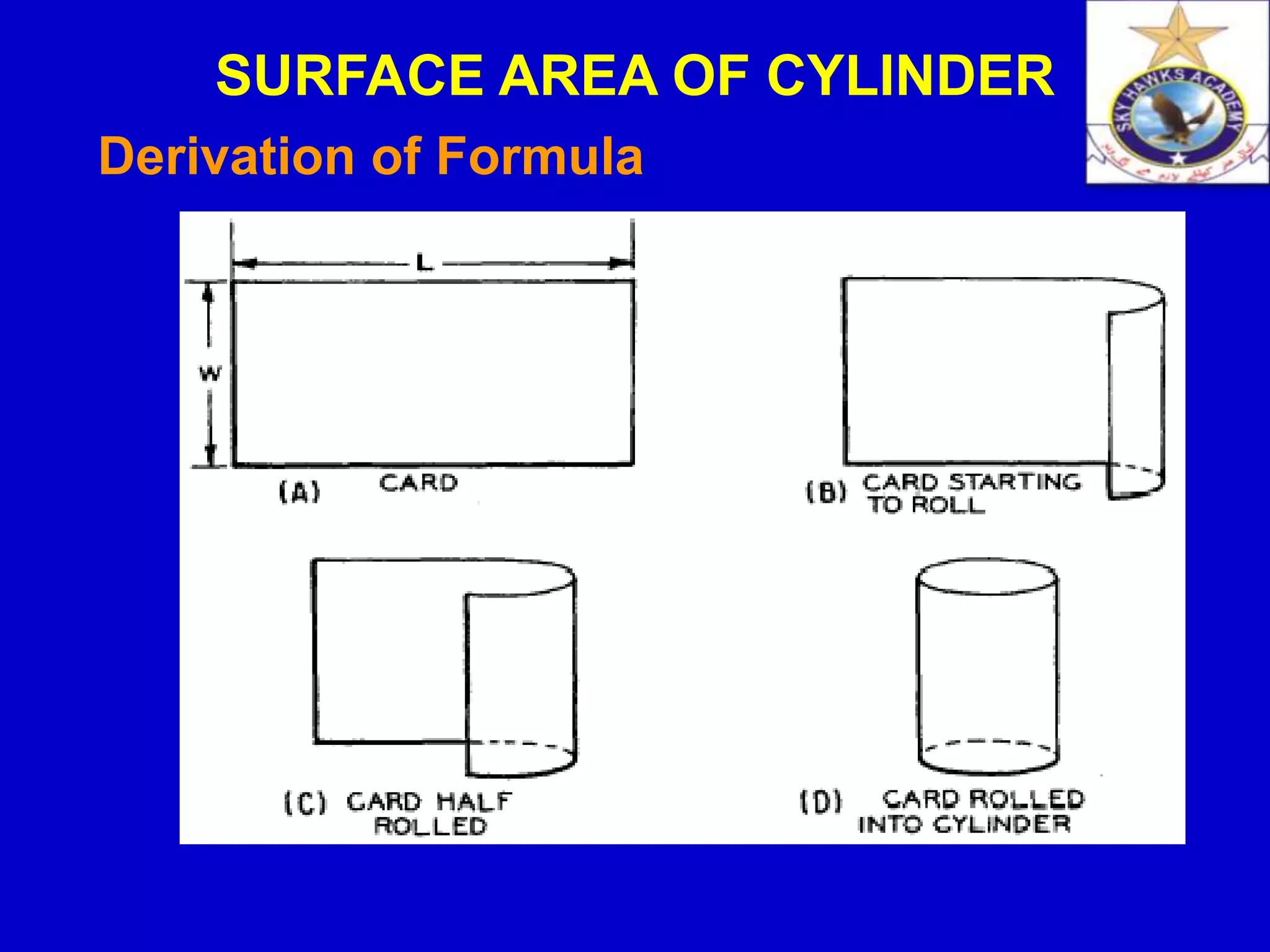
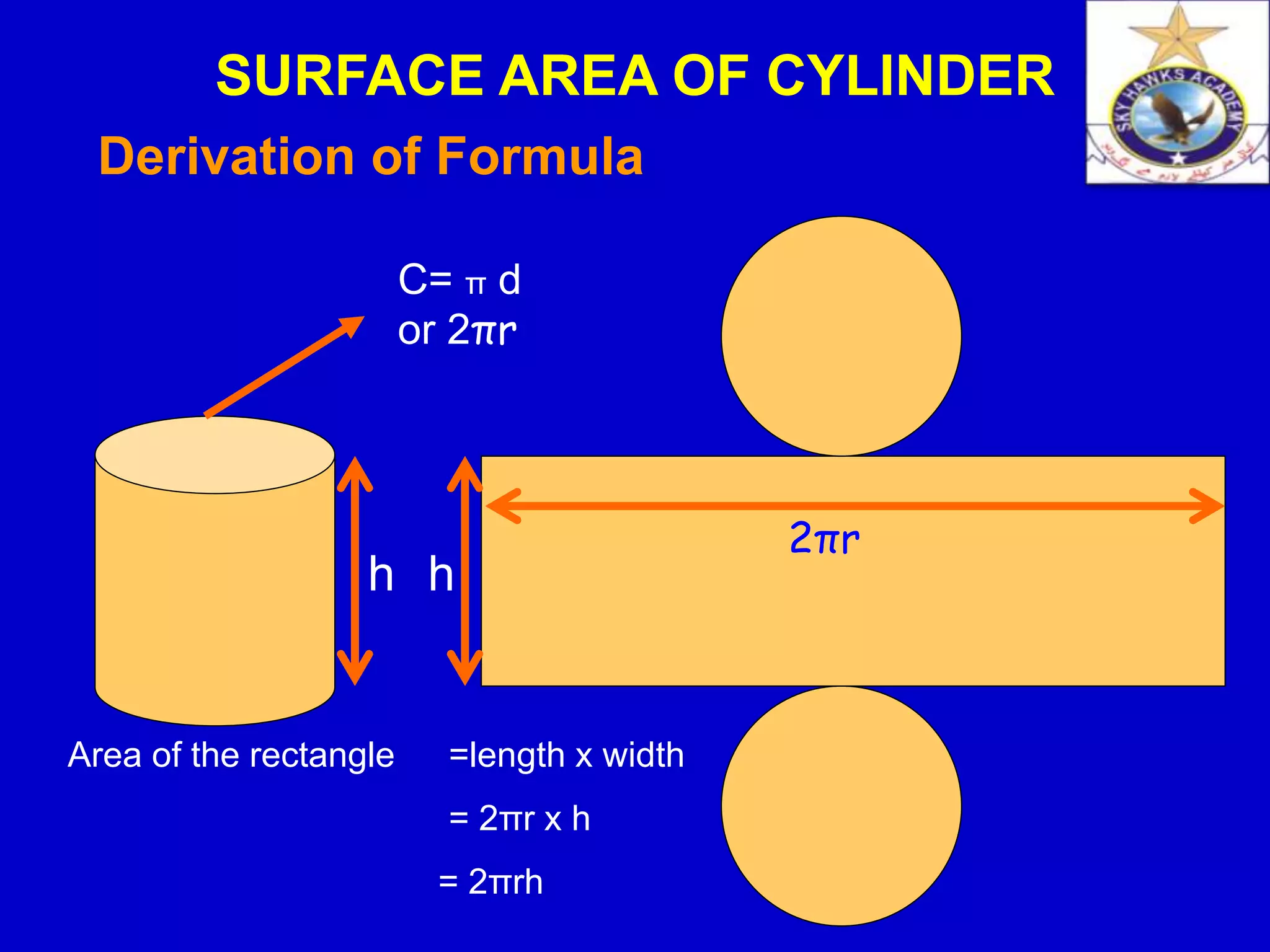
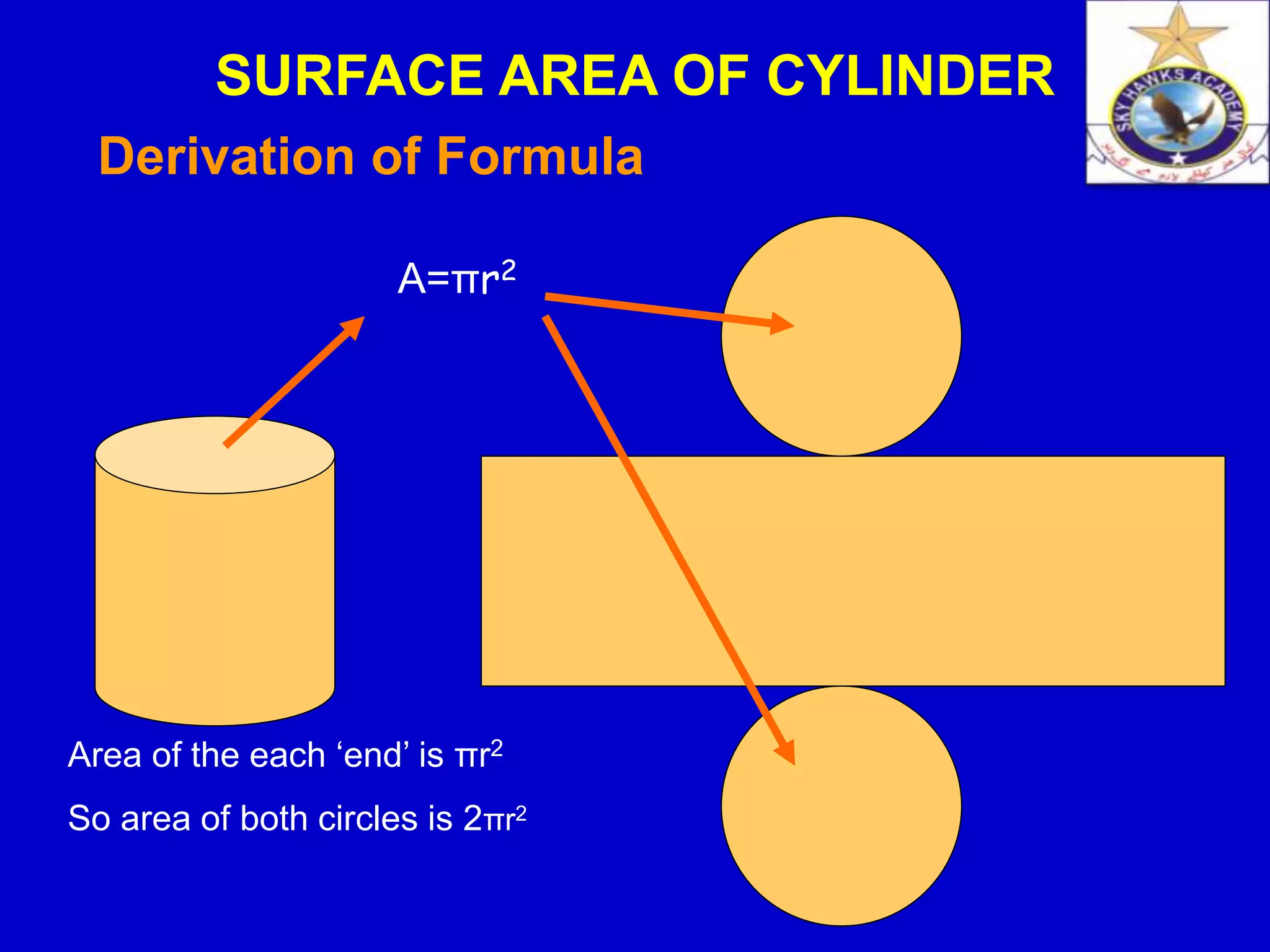
The document discusses the surface area of a cylinder. It defines a cylinder and derives the formula for calculating the surface area. The surface area depends on the radius and height of the cylinder. It is calculated by finding the area of the two circular bases plus the curved surface area, which has the shape of a rectangle when unfolded. Some examples are provided to demonstrate how to use the formula to find the surface area. Applications of cylinders in daily life are also mentioned.

2. SUBJECT : MATHEMATICS
CHAPTER (04/05) : VOLUME AND AREA OF
GEOMETRICAL FIGURES
LESSON NO : 03 OF 13
TOPIC : SURFACE AREA OF
CYLINDER

3. Q. What do we observe in this movie clip?
A. Construction of Cylinder

4. Q. How can we find out the cost for painting the
given cylinder if cost for unit square is given to us
A. By calculating surface area of given cylinder

5.  Definition of Cylinder
 Derivation of Formula
 Related Examples
 Applications
SURFACE AREA OF CYLINDER

6. Definition
The union of all line segments that connect
corresponding points on congruent circles in
parallel planes.
SURFACE AREA OF CYLINDER

7. SURFACE AREA OF CYLINDER
Derivation of Formula
Watch the clip carefully

8. Q. What are the factors on which surface area of
cylinder depends upon?
A. There are two factors :
• Height
• Radius
SURFACE AREA OF CYLINDER
Derivation of Formula

9. SURFACE AREA OF CYLINDER
Q. How many types of surfaces are there in
this cylinder ?
A. There are two surfaces in this cylinder:
• Circular surface
• Curved Surface
Q What type of shape is obtained if curved
surface unfolded ?
A. Rectangular shape
Derivation of Formula

10. SURFACE AREA OF CYLINDER
Derivation of Formula

11. Q What will be the length of this rectangle?
A. Circumference = 2r
Q. What will be the width of this rectangle?
A. Perpendicular distance between plane
circular surfaces = h
r2
h
SURFACE AREA OF CYLINDER
Derivation of Formula

12. SURFACE AREA OF CYLINDER
Q. What will be the area of this rectangle?
A. Length x Width = 2r x h = 2rh
r2
h 2rh
Derivation of Formula

13. SURFACE AREA OF CYLINDER
Q. What is the shape of plane surfaces of
a cylinder ?
A. Two circular surfaces
Q What will be the area of one circular
surface ?
A. r2
Q What will be the area of two circular
surfaces?
A. 2r2
r
r
r2
r2
Derivation of Formula

14. h h
C= π d
or 2πr
2πr
Area of the rectangle =length x width
= 2πr x h
= 2πrh
SURFACE AREA OF CYLINDER
Derivation of Formula

15. A=πr2
Area of the each ‘end’ is πr2
So area of both circles is 2πr2
SURFACE AREA OF CYLINDER
Derivation of Formula

16. πr2
Total surface area is
2πrh + 2πr2
πr2
2πrh
SURFACE AREA OF CYLINDER
Derivation of Formula

17. EXAMPLES

18. Example No. 1
The length of a cylinder is 20 cm and radius of its
base is 15 cm. Find the area of total surface of cylinder.
Solution
r = 15cm
h = 20cm
 = 3.145
Surface area of cylinder = 2r (r + h)
= 2 x 3.145 x 15 (15 + 20)
= 3300 cm2
SURFACE AREA OF CYLINDER
20cm
15cm

19. Length of a pipe is 3m and it’s radius is 14 cm.
Find the area of curved surface.
Solution
r = 14 cm
h = 3m = 300 cm
Area of curved surface = 2rh
= 2 x 3.145 x 14 x 300
= 26418 cm2
Example No. 2
SURFACE AREA OF CYLINDER
300cm
14cm

20. APPLICATIONS

21. Motion of Piston
DAILY LIFE APPLICATIONS OF CYLINDER

22. Cylinder Reconditioning
DAILY LIFE APPLICATIONS OF CYLINDER

23. Cylinder Bore Honing
DAILY LIFE APPLICATIONS OF CYLINDER

24.  Definition of Cylinder
 Derivation of Formula
 Related Examples
 Applications
SURFACE AREA OF CYLINDER

25. Q. How many types of surfaces are there in
this cylinder?
A. There are two surfaces in this cylinder:
• Circular surface
• Curved Surface
Q What type of shape is obtained if curved
surface unfolded ?
A. Rectangle
SURFACE AREA OF CYLINDER

26. Q What will be the length of this rectangle?
A. Circumference = 2r
Q. What will be the width of this rectangle?
A. Perpendicular distance between plane
circular surfaces = h
r2
h
SURFACE AREA OF CYLINDER

27. Q. In a factory 200 solid cylinders 4 ft long and 1.5 ft in
diameter have to be painted. What will be the cost of painting
the cylinders if cost for 1 ft2 is Rs.5?
SURFACE AREA OF CYLINDER

28. SURFACE AREA OF CYLINDER
Solution
Diameter = 1.5 ft
r = 0.75 ft
h = 4 ft
Surface area of one cylinder = 2r(r+h)
= 2 (3.14)(0.75) (0.75+4)
=2(3.14)(0.75)(4.75)
= 22.37 ft2
Surface area of 200 cylinders = 200 x 22.37
= 4474.5 ft2
Total cost @ Rs 5 per ft2 = 4474.5 x 5
= 22372.5 Rs

29. VOLUME OF CYLINDER