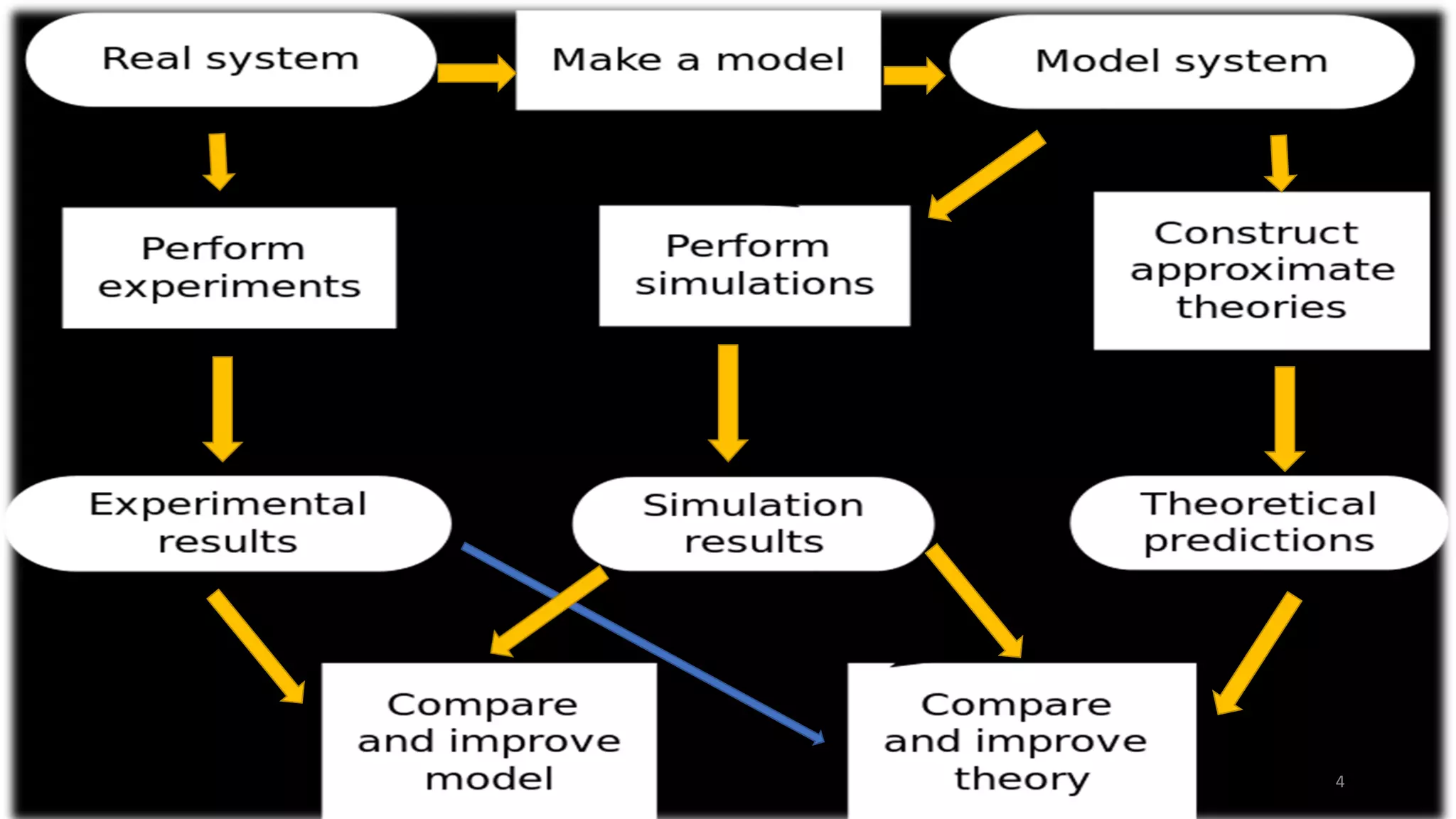
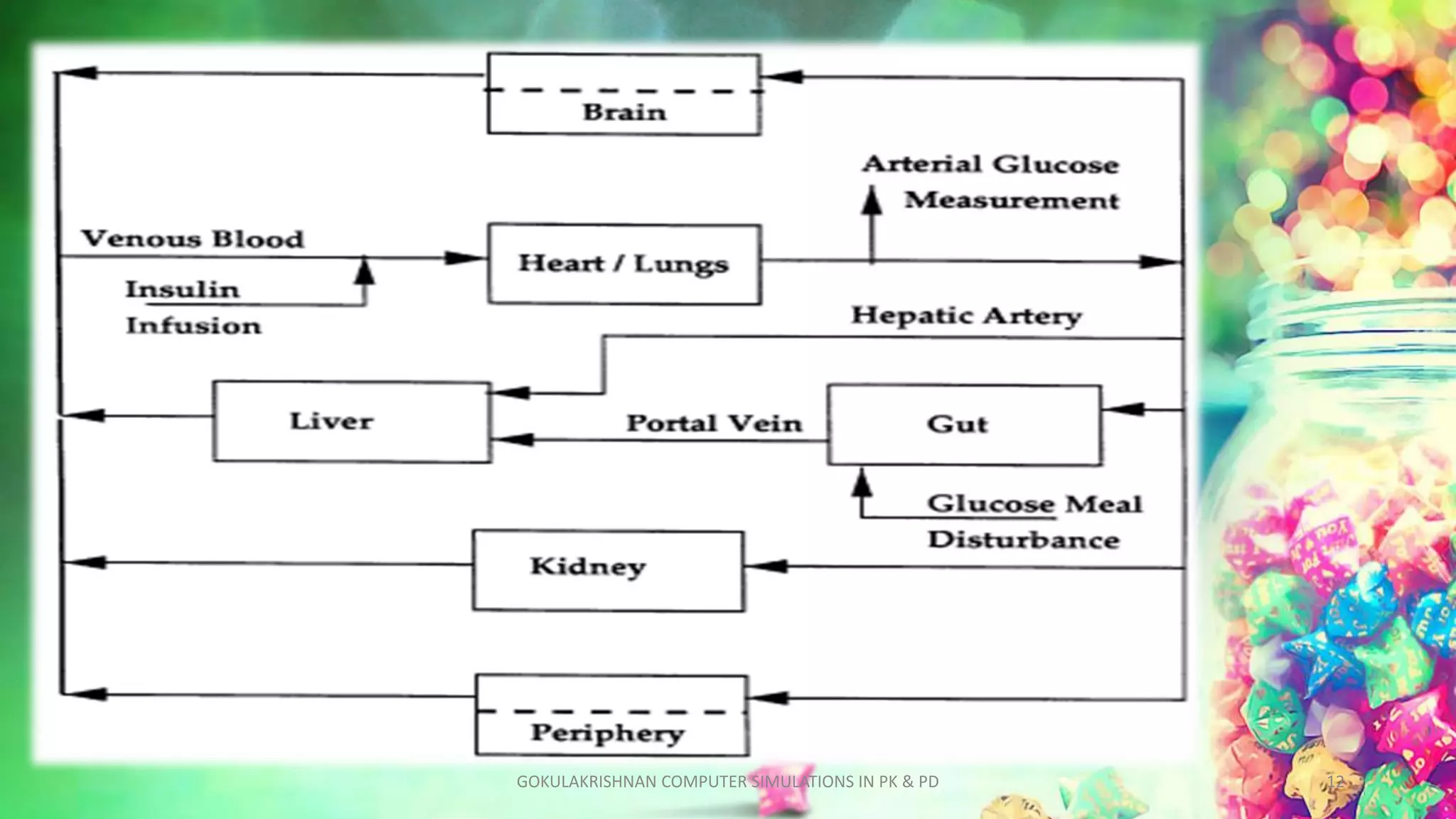
This document discusses computer simulations in pharmacokinetics and pharmacodynamics. It describes how whole organism, isolated tissue, and organ simulations work. For whole organism simulations, two approaches are used: lumped-parameter PK-PD modeling which uses differential equations to model the system over time, and physiological modeling which attempts to model interacting organs in detail. Isolated tissue and organ simulations are also discussed, focusing on models of the heart, liver, kidney and brain. The challenges of complexity and model selection are addressed.

1. S.GOKULAKRISHNAN
M.Pharm 1st year
Mother Theresa Post Graduate and Research Institute of Health Sciences
(A Government of Puducherry Institution)
COLLEGE OF PHARMACY
DEPARTMENT OF PHARMACEUTICS
Puducherry. GOKULAKRISHNAN COMPUTER SIMULATIONS IN PK & PD
COMPUTER SIMULATIONS IN
PHARMACOKINETICS &PHARMACODYNAMICS
1

2. CONTENTS:
1.INTRODUCTION
2.COMPUTER SIMULATION
3.WHOLE ORGANISM SIMULATION
4.ISOLATED TISSUE SIMULATION
5.ORGANS SIMULATION
GOKULAKRISHNAN COMPUTER SIMULATIONS IN PK & PD 2

3. INTRODUCTION
 A computer simulation or a computer model is a
computer program that attempts to simulate an abstract
model of a particular system.
 Computational resources available today, large-scale models
of the body can be used to produce realistic simulations.
 It involves the use of computer simulations of biological
systems,including cellular subsystems (such as the networks
of metabolites and enzymes which comprise metabolism,
signal transduction,pathways and gene regulatory networks),
to both analyze and visualize the complex connections of
these cellular processes.
GOKULAKRISHNAN COMPUTER SIMULATIONS IN PK & PD 3

4. GOKULAKRISHNAN COMPUTER SIMULATIONS IN PK & PD 4

5. WHOLE ORGANISM
SIMULATION
GOKULAKRISHNAN COMPUTER SIMULATIONS IN PK & PD 5

6. 1.Computer simulation being able to model the
whole organism is the essential goal of biocomputing.
2.In drug development, it provides the obligatory
handle to lead to response from exposure.
3.The intact organism can be mathematically
represented, a whole series of possibilities can be
brought into practice, such as the simulation of
clinical trials and of the prospective behavior of entire
populations.
GOKULAKRISHNAN COMPUTER SIMULATIONS IN PK & PD 6

7. GOKULAKRISHNAN COMPUTER SIMULATIONS IN PK & PD 7

8. IN WHOLE ORGANISM SIMULATION ,WHOLE BODY
SYSTEMS ARE USUALLY REPRESENTED IN ONE OF
TWO WAYS.
1.LUMPED-PARAMETER PK-PD MODEL
2.PHYSIOLOGICAL MODELING
GOKULAKRISHNAN COMPUTER SIMULATIONS IN PK & PD 8

9. LUMPED-PARAMETER PK-PD MODEL
{POPULATION PHARMACOKINETIC AND PHARMACODYNAMIC
MODELING }
o The lumped element model (also called lumped parameter model,
or component model) simplifies the description of
the behaviour of spatially distributed physical systems into a
topology consisting of discrete entities that approximate
the behaviour of the distributed system under certain assumptions.
o The purpose of this study is to characterize the pharmacokinetics
(PKs) and pharmacodynamics (PDs) of population by modeling
analysis and to predict proper dosage regimens.
o Plasma concentrations over time were best described by
a two‐compartment linear model and body weight was associated
with central volume of distribution.
GOKULAKRISHNAN COMPUTER SIMULATIONS IN PK & PD 9

10. oA relatively small number of differential equations,
between one and ten, is used to predict the system’s
behavior over time .
oOften, but not always, some variation of population PK-
PD predicated on nonlinear regression and nonlinear
mixed-effects models , is used to estimate both the
population parameter values and their statistical
distribution.
oThe same approach can be taken in reverse by using
models to generate synthetic data, ultimately performing a
full clinical trial simulation from first principles.
GOKULAKRISHNAN COMPUTER SIMULATIONS IN PK & PD 10

11. PHYSIOLOGICAL MODELING
oThis model brought into practice by physiologically based
pharmacokinetic (PBPK) models .
oThese models are still based on ordinary differential
equations,but they attempt to describe the organism and
especially the interacting organs with more detail, often by
increasing the number of differential equations (from 10 to
perhaps 30) and building appropriate interactions between
the organs that resemble their physical arrangement in the
organism being studied.
GOKULAKRISHNAN COMPUTER SIMULATIONS IN PK & PD 11

12. GOKULAKRISHNAN COMPUTER SIMULATIONS IN PK & PD 12

13. oModel selection is driven by some kind of parsimony criteria on
that balances model complexity with the actual information
content provided by the measurements.
oA consensus workshop developed some time ago a set of
“good practices” that can serve as guidance to model
development, selection, and application.
oPbpk models come at the problem from a different angle.
oPbpk models can suffer greatly in their predictive power if
their parameterization is inaccurate, poorly specified, or not
well tailored to the particular drug.
oIt is interesting to note that the foremost challenges for the
detailed modeling of the intact organism (computing
time, complexity of interactions, model selection)
GOKULAKRISHNAN COMPUTER SIMULATIONS IN PK & PD 13

14. ISOLATED TISSUE
&
ORGANS SIMULATION
GOKULAKRISHNAN COMPUTER SIMULATIONS IN PK & PD 14

15. oThe heart and the liver were historically the organs most
extensively investigated ,although the kidney and brain
have also been the subjects of mathematical modeling
research.
oMany of the computer simulations for the heart and liver
were carried out with distributed blood tissue exchange
(BTEX) models , because the increased level of detail and
temporal resolution certainly makes the good mixing and
uniformity hypotheses at the basis of lumped parameter
models less tenable.
oIt can be speculated that the integration of organ-specific
modeling with the above whole organism models would
result in improvements for the PBPK approach through
“better” (i.e.,more physiologically sensible and plausible)
models of individual organs.
GOKULAKRISHNAN COMPUTER SIMULATIONS IN PK & PD 15

16. oThe main challenge in doing so is the required shift from
lumped to distributed parameter models.
oNational Institute for General Medical Sciences at the NIH,
the Center for Modeling Integrated Metabolic Systems
(MIMS) , has as its mission the development and integration
of in vivo, organ-specific mathematical models that can
successfully predict behaviors for a range of parameters,
including rest and exercise and various pathophysiological
conditions.
oMicrocirculation Physiome and the Cardiome are other
multicenter projects focused on particular aspects of the
Physiome undertaking.
oThere is an enormous variety of software for
pharmacokinetic and pharmacodynamic simulations.
GOKULAKRISHNAN COMPUTER SIMULATIONS IN PK & PD 16

17. oThe physiome of an individual's or species' physiological
state is the description of its functional behavior.
oThe physiome describes the physiological dynamics of the
normal intact organism and is built upon information and
structure (genome, proteome, and morphome).
GOKULAKRISHNAN COMPUTER SIMULATIONS IN PK & PD 17

18. GOKULAKRISHNAN COMPUTER SIMULATIONS IN PK & PD 18

19. REFERENCES
1.Modeling and Simulation of Soft Tissue
Deformation{https://link.springer.com/chapter/
10.1007/978-3-642-41083-3_25}.
2.COMPUTER APPLICATIONS IN
PHARMACEUTICAL RESEARCH AND
DEVELOPMENT BY SEAN EKINS, M.SC., PH.D.,
D.SC.
GOKULAKRISHNAN COMPUTER SIMULATIONS IN PK & PD 19

20. THANK YOU
GOKULAKRISHNAN COMPUTER SIMULATIONS IN PK & PD 20