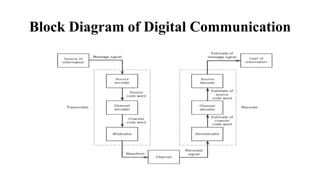
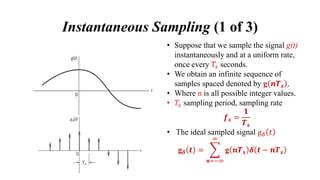
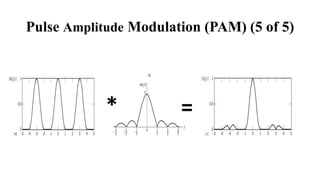
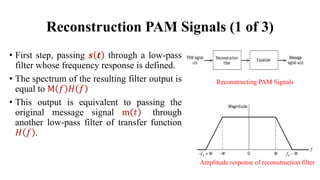
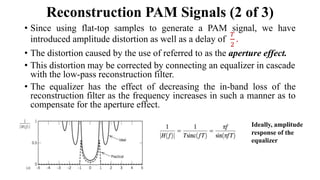
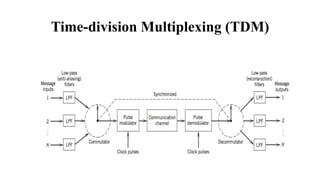
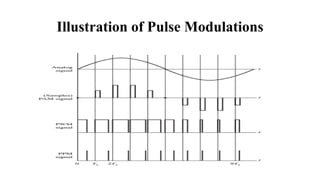
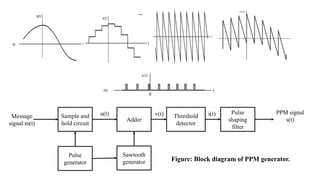
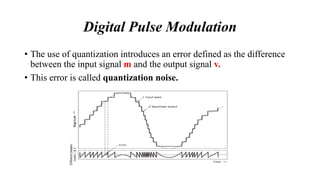
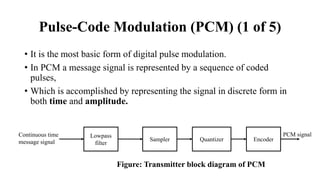
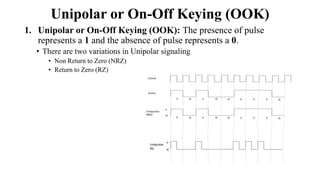
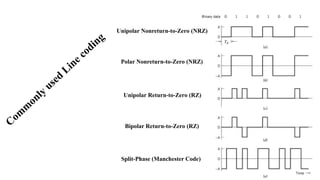
The document provides a comprehensive overview of pulse and digital modulation techniques, detailing the fundamentals of digital communication, sampling methods, and various modulation techniques such as Pulse Amplitude Modulation (PAM), Pulse Width Modulation (PWM), and Pulse Position Modulation (PPM). It also explores concepts like quantization, digital pulse modulation, and encoding schemes such as Pulse Code Modulation (PCM) and Delta Modulation (DM). Additionally, the document covers key aspects of digital modulation techniques including Amplitude Shift Keying (ASK), Frequency Shift Keying (FSK), and Phase Shift Keying (PSK).