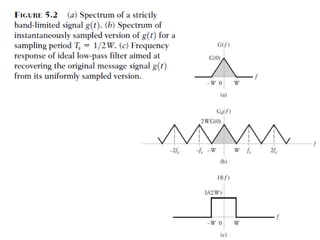
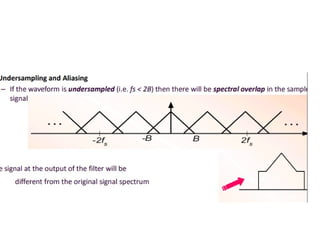
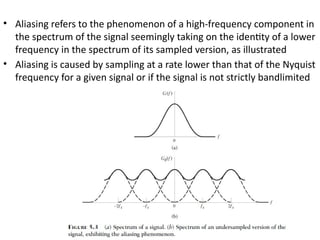
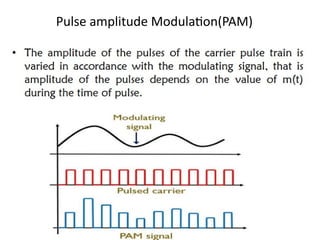
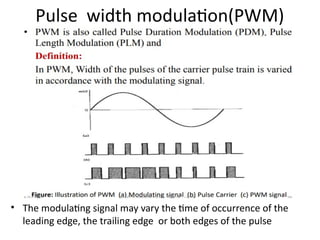
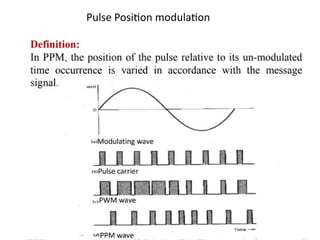
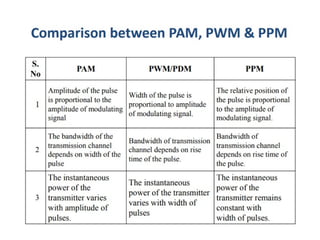
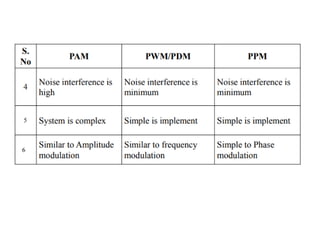
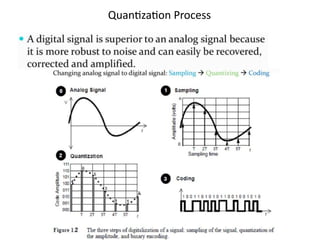
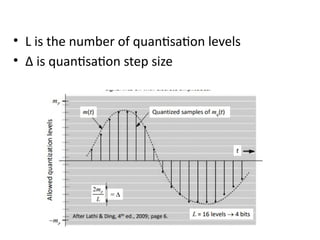
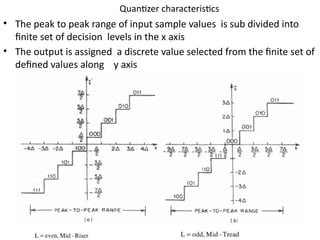
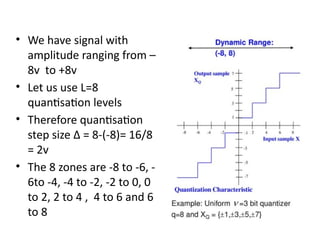
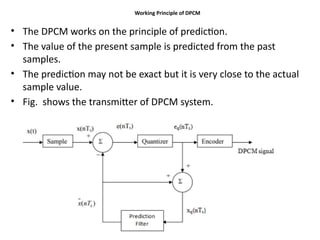
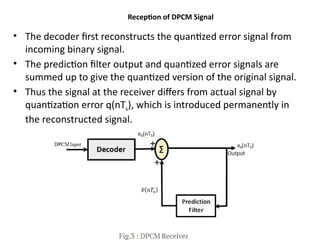
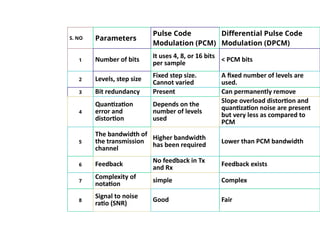
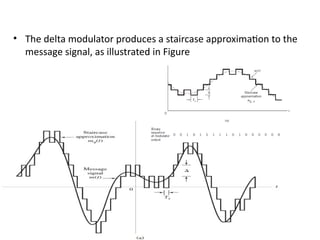
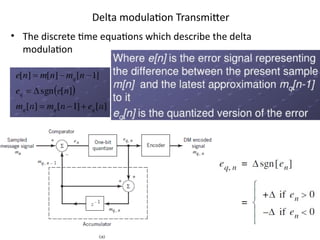
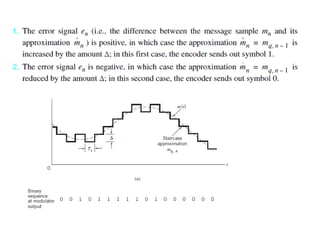
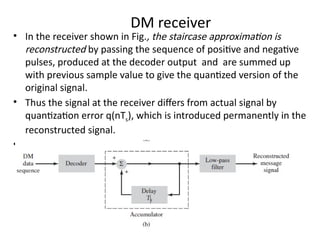
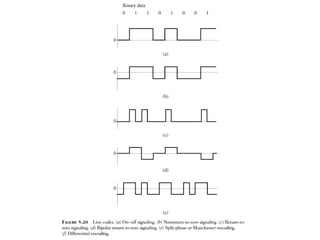
mod2dsssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssss







![Sampling
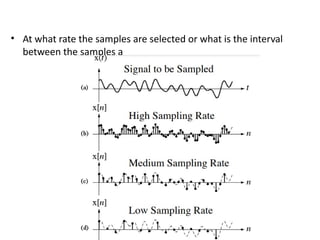
• Sampling is the processes of converting continuous -time analog
signal, x (t), into a discrete-time signal x[n] by taking the “samples”
at discrete-time intervals
• An analog signal is converted into a corresponding sequence of
samples that are usually spaced uniformly in time.](https://image.slidesharecdn.com/module2-250802140237-016a9811/85/Module2-pptxwewewewewewewewewewewewewewewewe-8-320.jpg)