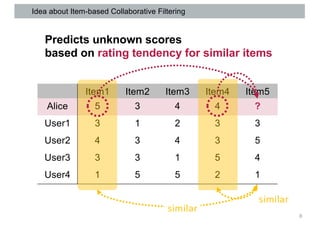
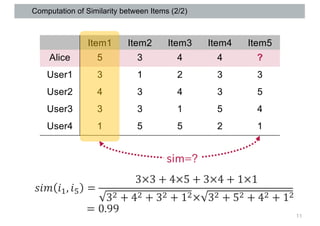
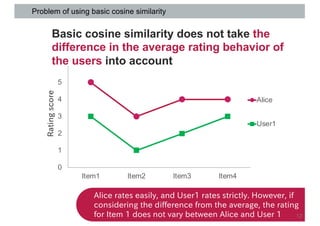
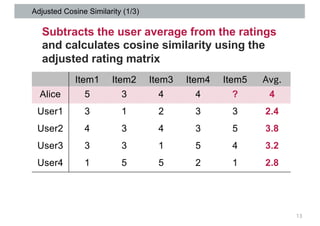
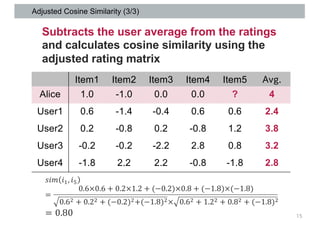
This document discusses item-based collaborative filtering for recommender systems. It describes how item-based collaborative filtering works by predicting a target user's rating for an item based on the ratings of similar items. It highlights advantages over user-based filtering like lower computational cost and more stable similarity computations. Key aspects covered include using cosine similarity to calculate item similarities, adjusting for individual rating biases, selecting the top K similar items, and predicting ratings based on similar items' ratings.

1. Item-based
Collaborative Filtering
Yusuke Yamamoto
Lecturer, Faculty of Informatics
yusuke_yamamoto@acm.org
Data Engineering （Recommender Systems 2）
2019.10.28

2. 1
2
Problems on User-based
Collaborative Filtering

3. User-based Collaborative Filtering
3
Predicts a target user’s rating for an item
based on rating tendency of similar users
𝑝𝑟𝑒𝑑𝑖𝑐𝑡 𝑢), 𝑖 = 𝑟,-
+
∑,∈12
𝑠𝑖𝑚(𝑢), 𝑢) 7 (𝑟,,8 − 𝑟,-
)
∑,∈12
𝑠𝑖𝑚(𝑢), 𝑢)
Item5 sim Average Rating
Alice ? 1 4
User1 3 0.85 2.4
User2 5 0.71 3.8
Similar
users

4. Computation of similarity between users
4
Pearson’s correlation coefficient
𝑠𝑖𝑚 𝑢), 𝑢: =
∑8∈;(𝑟,-,8 − 𝑟,-
)(𝑟,<,8 − 𝑟,<
)
∑8∈; 𝑟,-,8 − 𝑟,-
=
∑8∈; 𝑟,<,8 − 𝑟,<
=
Item1 Item2 Item3 Item4
Alice 5 3 4 4
User1 3 1 2 3
User2 4 3 4 3
User3 3 3 1 5
User4 1 5 5 2
sim=0.71
sim=-0.79

5. Problems on User-based Collaborative Filtering (1/2)
5
Item1 Item2 Item3 Item4 item5 item6
Bob 3 2
User1 3 1 2 3
User2 4 3 4 3
User3 3 3 1 5
User4 1 5 5 2 5
• It is rare that two users rated the same item
• User similarity drastically changes if a few ratings are added
Impossible to
compute similarity
Is it possible to compute precise user
similarity by using rating scores for only one
common item?
If users haven’t rate the same items yet,
user similarity cannot be computed

6. Problems on User-based Collaborative Filtering (2/2)
6
#Users >> #Items
• In general, the number of users are much bigger than that of items
• Big computational cost of nearest neighbors (similar users)
Unstable user preference
User preferences (user features) often change, while item features
do not often change

7. 2
7
Item-based
Collaborative Filtering

8. Idea about Item-based Collaborative Filtering
8
Item1 Item2 Item3 Item4 Item5
Alice 5 3 4 4 ?
User1 3 1 2 3 3
User2 4 3 4 3 5
User3 3 3 1 5 4
User4 1 5 5 2 1
similar
Predicts unknown scores
based on rating tendency for similar items
similar

9. Advantages of Item-based Collaborative Filtering
9
Computational cost
In general, the number of items is much less than that of users, and so
the item-based CF’s computational cost is much smaller than the user-
based CF’s
Stable similarity computation
• Item features (vectors) do not often change and are stable
• Compared to user features (vectors) on a rating matrix, features
(vectors) have less N/A dimensions.
• It is possible to compute similarity between items by using enough
information

10. Computation of Similarity between Items (1/2)
10
Cosine similarity
𝑠𝑖𝑚 𝑖), 𝑖: = cos 𝜃 =
𝒗8-
7 𝒗8<
𝒗8-
∗ |𝒗8<
|
• Focuses on the angle between two vectors
• The similarity ranges between 0 and 1
• Best performance for item similarity calculation
：Item a, b𝑖), 𝑖:
：Item a, b’s rating vector𝒗8-
, 𝒗8-
0
:Angle between 𝒗8-
, 𝒗8-
𝜃
：Vector 𝒗’s length|𝒗|

11. Computation of Similarity between Items (2/2)
11
Item1 Item2 Item3 Item4 Item5
Alice 5 3 4 4 ?
User1 3 1 2 3 3
User2 4 3 4 3 5
User3 3 3 1 5 4
User4 1 5 5 2 1
sim=?
𝑠𝑖𝑚 𝑖E, 𝑖F =
3×3 + 4×5 + 3×4 + 1×1
3= + 4= + 3= + 1=× 3= + 5= + 4= + 1=
= 0.99

12. Problem of using basic cosine similarity
12
0
1
2
3
4
5
6
Item1 Item2 Item3 Item4
Alice
User1
Ratingscore
Basic cosine similarity does not take the
difference in the average rating behavior of
the users into account
Alice rates easily, and User1 rates strictly. However, if
considering the difference from the average, the rating
for Item 1 does not vary between Alice and User 1

13. Adjusted Cosine Similarity (1/3)
13
Item1 Item2 Item3 Item4 Item5 Avg.
Alice 5 3 4 4 ? 4
User1 3 1 2 3 3 2.4
User2 4 3 4 3 5 3.8
User3 3 3 1 5 4 3.2
User4 1 5 5 2 1 2.8
Subtracts the user average from the ratings
and calculates cosine similarity using the
adjusted rating matrix

14. Adjusted Cosine Similarity (2/3)
14
Subtracts the user average from the ratings
and calculates cosine similarity using the
adjusted rating matrix
Item1 Item2 Item3 Item4 Item5 Avg.
Alice 5 3 4 4 ? 4
User1 3 1 2 3 3 2.4
User2 4 3 4 3 5 3.8
User3 3 3 1 5 4 3.2
User4 1 5 5 2 1 2.8
-4 -4 -4 -4
-2.4 -2.4 -2.4 -2.4
-3.8 -3.8 -3.8 -3.8
-3.2 -3.2 -3.2 -3.2
-2.8 -2.8 -2.8 -2.8
-2.4
-3.8
-3.2
-2.8

15. Adjusted Cosine Similarity (3/3)
15
Subtracts the user average from the ratings
and calculates cosine similarity using the
adjusted rating matrix
𝑠𝑖𝑚 𝑖E, 𝑖F
=
0.6×0.6 + 0.2×1.2 + (−0.2)×0.8 + (−1.8)×(−1.8)
0.6= + 0.2= + (−0.2)=+(−1.8)=× 0.6= + 1.2= + 0.8= + (−1.8)=
= 0.80
Item1 Item2 Item3 Item4 Item5 Avg.
Alice 1.0 -1.0 0.0 0.0 ? 4
User1 0.6 -1.4 -0.4 0.6 0.6 2.4
User2 0.2 -0.8 0.2 -0.8 1.2 3.8
User3 -0.2 -0.2 -2.2 2.8 0.8 3.2
User4 -1.8 2.2 2.2 -0.8 -1.8 2.8

16. Rating Prediction based on Item Similarity
16
Prediction Function (predicted scores are adjusted)
𝑝𝑟𝑒𝑑𝑖𝑐𝑡 𝑢), 𝑖R =
∑8∈;2
𝑠𝑖𝑚(𝑖R, 𝑖) 7 𝑟,-,8
∑8∈;2
𝑠𝑖𝑚(𝑖R, 𝑖)
： target user a𝑢)
𝑟,,8 ： rating score of user u for item i
𝑖R： target item t
𝐼T ： a set of similar items for a target item

17. Selection of Similar Item (nearest neighbor items)
17
Set a threshold for item similarity
Focus on top K similar items （kNN method）
If an item has higher similarity than a threshold,
it can be regarded as a “similar” item
• If an item ranks at the top K similarity, it can be regarded
as a similar item
• K is often set to between 50 〜 200

18. Summary of Item-based Collaborative Filtering
18
Basic Approach
• Item similarities are obtained from a rating matrix
• Based on rating scores of similar items, systems predict
a rating score of target user for a target item
Similarity Calculation
Cosine similarity is known best in practice
Selection of Similar Items
Top K items with high similarity are often selected as
similar items