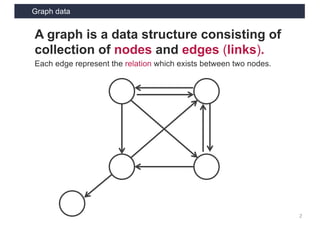
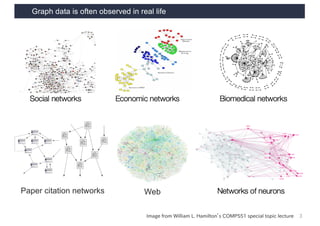
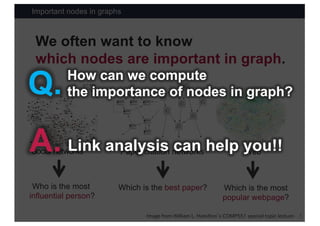
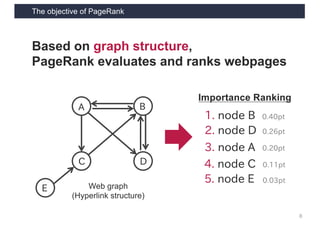
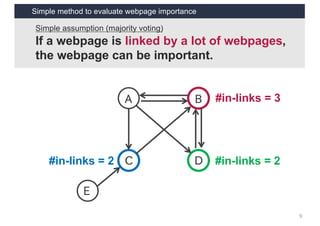
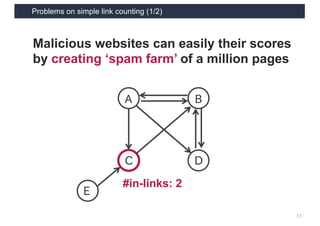
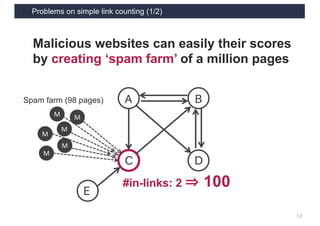
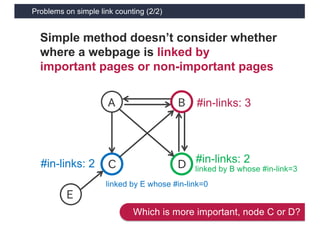
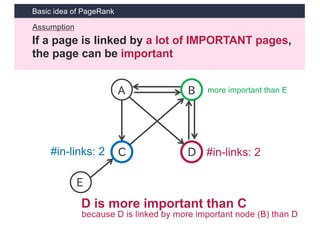
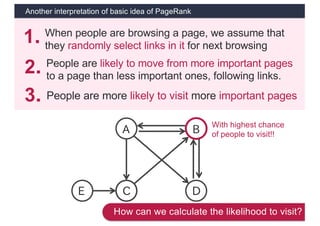
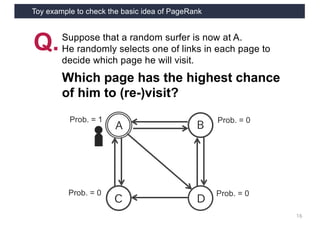
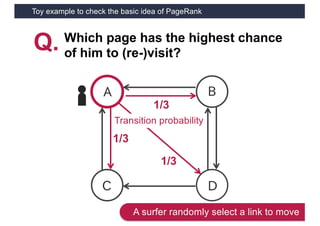
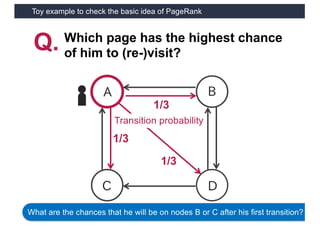
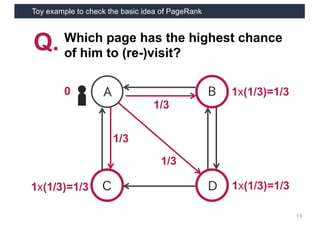
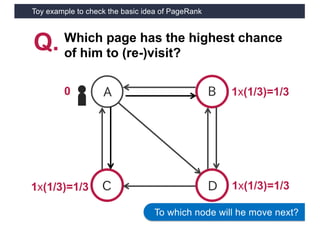
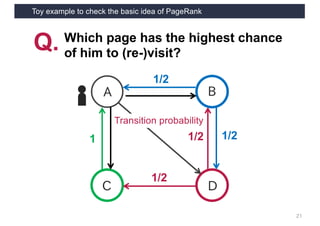
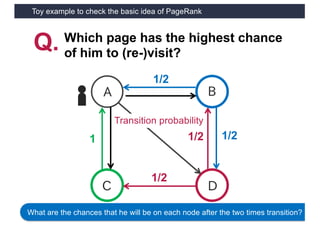
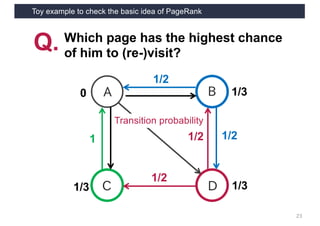
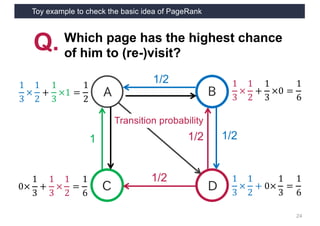
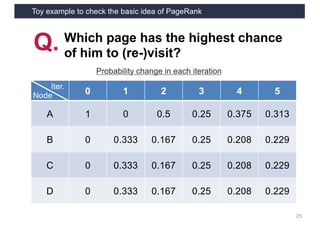
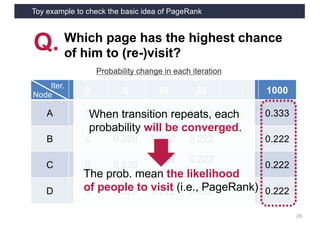
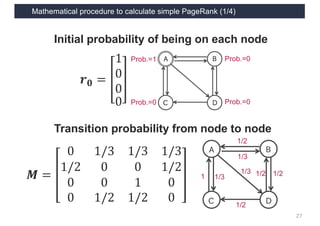
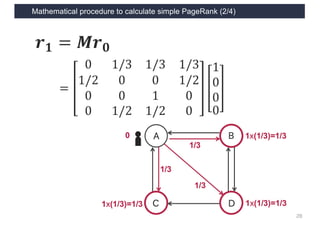
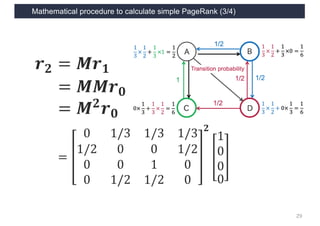
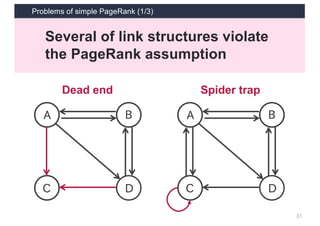
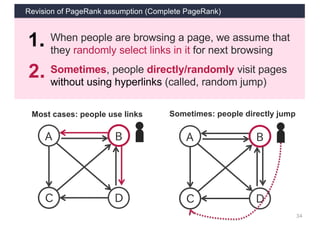
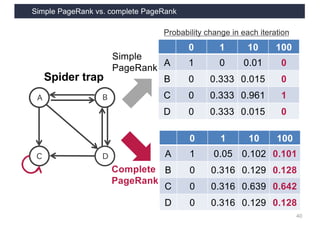
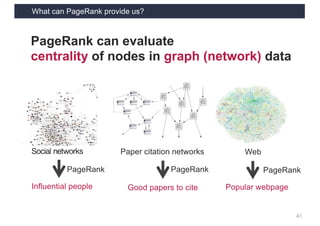
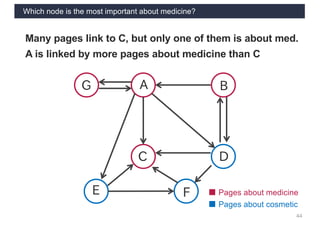
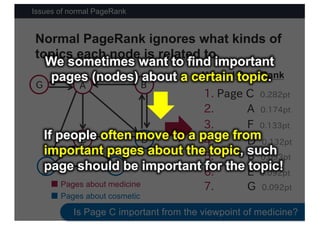
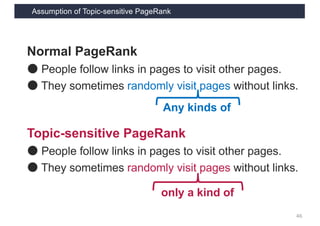
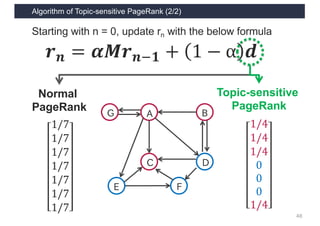
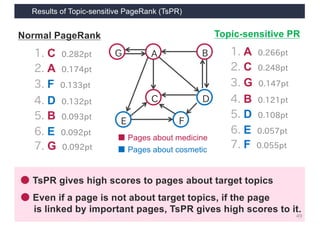
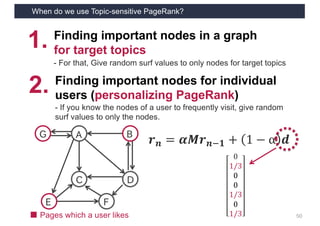
This document discusses link analysis and PageRank, an algorithm for identifying important nodes in large network graphs. It begins with an overview of graph data structures and the goal of identifying influential nodes. It then introduces PageRank, explaining its basic assumptions and showing examples of how it calculates node importance scores. The document discusses problems with the initial PageRank approach and how it was improved with the Complete PageRank algorithm. Finally, it briefly introduces Topic-sensitive PageRank, which aims to identify important nodes related to specific topics.

1. Link Analysis:
Find important nodes in large-scale network
Yusuke Yamamoto
Lecturer, Faculty of Informatics
yusuke_yamamoto@acm.org
Data Engineering （Recommender Systems 4）
2019.11.18

2. Graph data
2
A graph is a data structure consisting of
collection of nodes and edges (links).
Each edge represent the relation which exists between two nodes.

3. Graph data is often observed in real life
3Image from William L. Hamilton’s COMP551 special topic lecture
Paper citation networks Web

4. Important nodes in graphs
4Image from William L. Hamilton’s COMP551 special topic lecture
We often want to know
which nodes are important in graph.
Who is the most
influential person?
Which is the best paper? Which is the most
popular webpage?
Paper citation networks Web

5. Important nodes in graphs
5Image from William L. Hamilton’s COMP551 special topic lecture
We often want to know
which nodes are important in graph.
Who is the most
influential person?
Which is the best paper? Which is the most
popular webpage?
Paper citation networks Web
How can we compute
the importance of nodes in graph?Q.
Link analysis can help you!!A.

6. What do we learn today?
6
PageRank
Topic-sensitive PageRank
1.
2.

7. 1
7
PageRank
Google introduced a new method to evaluate webpages

8. The objective of PageRank
8
A
C D
B
E
Importance Ranking
1. node B
2. node D
3. node A
4. node C
5. node E
0.40pt
0.26pt
0.20pt
0.11pt
0.03pt
Based on graph structure,
PageRank evaluates and ranks webpages
Web graph
(Hyperlink structure)

9. Simple method to evaluate webpage importance
9
Simple assumption (majority voting)
If a webpage is linked by a lot of webpages,
the webpage can be important.
A
C D
B
E
#in-links = 3
#in-links = 2 #in-links = 2

10. Simple method to evaluate webpage importance
10
Simple assumption (majority voting)
If a webpage is linked by a lot of webpages,
the webpage can be important.
A
C D
B
E
#in-links = 3
#in-links = 2 #in-links = 2
Is this assumption enough OK?

11. Problems on simple link counting (1/2)
11
A
C D
B
E
Malicious websites can easily their scores
by creating ‘spam farm’ of a million pages
#in-links: 2

12. Problems on simple link counting (1/2)
12
A
C D
B
E
#in-links: 2 ⇒ 100
Malicious websites can easily their scores
by creating ‘spam farm’ of a million pages
M
M
M
M
M
M
Spam farm (98 pages)

13. Problems on simple link counting (2/2)
13
Simple method doesn’t consider whether
where a webpage is linked by
important pages or non-important pages
A
C D
B
E
#in-links: 3
#in-links: 2 #in-links: 2
linked by B whose #in-link=3
linked by E whose #in-link=0
Which is more important, node C or D?

14. Basic idea of PageRank
If a page is linked by a lot of IMPORTANT pages,
the page can be important
Assumption
A
C D
B
E
more important than E
#in-links: 2 #in-links: 2
D is more important than C
because D is linked by more important node (B) than D

15. Another interpretation of basic idea of PageRank
15
People are more likely to visit more important pages
1．When people are browsing a page, we assume that
they randomly select links in it for next browsing
2．People are likely to move from more important pages
to a page than less important ones, following links.
A
C D
B
E
With highest chance
of people to visit!!
How can we calculate the likelihood to visit?
3．

16. Toy example to check the basic idea of PageRank
16
A
C D
B
Q.Suppose that a random surfer is now at A.
He randomly selects one of links in each page to
decide which page he will visit.
Which page has the highest chance
of him to (re-)visit?
Prob. = 1
Prob. = 0
Prob. = 0
Prob. = 0

17. Toy example to check the basic idea of PageRank
17
A
C D
B
Q. Which page has the highest chance
of him to (re-)visit?
A surfer randomly select a link to move
1/3
1/3
Transition probability
1/3

18. Toy example to check the basic idea of PageRank
18
A
C D
B
Q. Which page has the highest chance
of him to (re-)visit?
1/3
1/3
Transition probability
1/3
What are the chances that he will be on nodes B or C after his first transition?

19. Toy example to check the basic idea of PageRank
19
A
C D
B
Q. Which page has the highest chance
of him to (re-)visit?
1x(1/3)=1/3
1x(1/3)=1/3 1x(1/3)=1/3
0
1/3
1/3
1/3

20. Toy example to check the basic idea of PageRank
20
A
C D
B
Q. Which page has the highest chance
of him to (re-)visit?
1x(1/3)=1/3
1x(1/3)=1/3 1x(1/3)=1/3
0
To which node will he move next?

21. Toy example to check the basic idea of PageRank
21
A
C D
B
Q. Which page has the highest chance
of him to (re-)visit?
1/2
1/21
Transition probability
1/2
1/2

22. Toy example to check the basic idea of PageRank
22
A
C D
B
Q. Which page has the highest chance
of him to (re-)visit?
1/2
1/21
Transition probability
1/2
1/2
What are the chances that he will be on each node after the two times transition?

23. Toy example to check the basic idea of PageRank
23
A
C D
B
Q. Which page has the highest chance
of him to (re-)visit?
1/2
1/21
Transition probability
1/2
1/2
1/3
1/3 1/3
0

24. Toy example to check the basic idea of PageRank
24
A
C D
B
Q. Which page has the highest chance
of him to (re-)visit?
1/2
1/21
Transition probability
1
3
×
1
2
+
1
3
×1 =
1
2
1
3
×
1
2
+
1
3
×0 =
1
6
1
3
×
1
2
+ 0×
1
3
=
1
6
0×
1
3
+
1
3
×
1
2
=
1
6
1/2
1/2

25. Toy example to check the basic idea of PageRank
25
Q. Which page has the highest chance
of him to (re-)visit?
0 1 2 3 4 5
A 1 0 0.5 0.25 0.375 0.313
B 0 0.333 0.167 0.25 0.208 0.229
C 0 0.333 0.167 0.25 0.208 0.229
D 0 0.333 0.167 0.25 0.208 0.229
Node
Iter.
Probability change in each iteration

26. Toy example to check the basic idea of PageRank
26
Q. Which page has the highest chance
of him to (re-)visit?
0 5 10 20 … 1000
A 1 0.313 0.334 0.333 0.333
B 0 0.229 0.222 0.222 0.222
C 0 0.229
0.222 0.222
0.222
D 0 0.229 0.222 0.222 0.222
Node
Iter.
When transition repeats, each
probability will be converged.
The prob. mean the likelihood
of people to visit (i.e., PageRank)
Probability change in each iteration

27. Mathematical procedure to calculate simple PageRank (1/4)
27
Initial probability of being on each node
𝒓 𝟎 =
1
0
0
0
Transition probability from node to node
𝑴 =
0 1/3 1/3 1/3
1/2 0 0 1/2
0 0 1 0
0 1/2 1/2 0
A
C D
B
Prob.=1
Prob.=0
Prob.=0
Prob.=0
1/2
1/3
1/3
1/3
1/2
1/2 1/21

28. Mathematical procedure to calculate simple PageRank (2/4)
28
𝒓 𝟏 = 𝑴𝒓 𝟎
=
0 1/3 1/3 1/3
1/2 0 0 1/2
0 0 1 0
0 1/2 1/2 0
1
0
0
0

29. Mathematical procedure to calculate simple PageRank (3/4)
29
𝒓 𝟐 = 𝑴𝒓 𝟏
=
0 1/3 1/3 1/3
1/2 0 0 1/2
0 0 1 0
0 1/2 1/2 0
𝟐
1
0
0
0
= 𝑴𝑴𝒓 𝟎
= 𝑴 𝟐
𝒓 𝟎

30. Mathematical procedure to calculate simple PageRank (4/4)
30
𝒓 𝒏 = 𝑴𝒓 𝒏1𝟏
= 𝑴𝑴𝒓 𝒏1𝟐
= 𝑴 𝟐 𝒓 𝒏1𝟐
= 𝑴 𝒏 𝒓 𝟎
…
If n is enough large or rn has converged, we think
rn represents the likelihood of people to visit

31. Problems of simple PageRank (1/3)
31
A
C D
B A
C D
B
Dead end Spider trap
Several of link structures violate
the PageRank assumption

32. Problems of simple PageRank (2/3)
32
A
C D
B
Dead end
Several of link structures violate
the PageRank assumption
0 1 10 100
A 1 0 0.01 0
B 0 0.333 0.015 0
C 0 0.333 0.015 0
D 0 0.333 0.015 0
Probability change in each iteration

33. Problems of simple PageRank (3/3)
33
A
C D
B
Spider trap
Several of link structures violate
the PageRank assumption
0 1 10 100
A 1 0 0.01 0
B 0 0.333 0.015 0
C 0 0.333 0.961 1
D 0 0.333 0.015 0
Probability change in each iteration

34. Revision of PageRank assumption (Complete PageRank)
34
1．When people are browsing a page, we assume that
they randomly select links in it for next browsing
2．Sometimes, people directly/randomly visit pages
without using hyperlinks (called, random jump)
A
C D
B
Most cases: people use links
A
C D
B
Sometimes: people directly jump

35. Algorithm of complete PageRank (1/5)
35
𝒓 𝒏 = 𝜶𝑴𝒓 𝒏1𝟏 + 1 − α 𝒅
2．Starting with n = 0, update rn with the below formula
Corresponds to the case where
people use links to visit pages
Corresponds to the case where
people directly visit pages
1． Initialize r0 (randomly assign values to r0).
Set transition Matrix M and random surf vector d

36. Algorithm of complete PageRank (2/5)
36
𝒓 𝒏 = 𝜶𝑴𝒓 𝒏1𝟏 + 1 − α 𝒅
Transition matrix
(which derived from link structure)
0 1/3 1/3 1/3
1/2 0 0 1/2
0 0 0 0
0 1/2 1/2 0
A
C D
B
1/3
1/3
1/3
1/2
1/2 1/2
2．Starting with n = 0, update rn with the below formula
1． Initialize r0 (randomly assign values to r0).
Set transition Matrix M and random surf vector d

37. Algorithm of complete PageRank (3/5)
37
𝒓 𝒏 = 𝜶𝑴𝒓 𝒏1𝟏 + 1 − α 𝒅
Random surf vector of
people to directly visit pages
(uniform distribution of prob.)
1/4
1/4
1/4
1/4
A
C D
B
2．Starting with n = 0, update rn with the below formula
1． Initialize r0 (randomly assign values to r0).
Set transition Matrix M and random surf vector d

38. Algorithm of complete PageRank (4/5)
38
𝒓 𝒏 = 𝜶𝑴𝒓 𝒏1𝟏 + 1 − α 𝒅
Probabilities (parameters) to decide
which of the two modes people use.
(Empirically, α is set in the range 0.8 to 0.9)
2．Starting with n = 0, update rn with the below formula
1． Initialize r0 (randomly assign values to r0).
Set transition Matrix M and random surf vector d

39. Algorithm of complete PageRank (5/5)
39
𝒓 𝒏 = 𝜶𝑴𝒓 𝒏1𝟏 + 1 − α 𝒅
2．Starting with n = 0, update rn with the below formula
1． Initialize r0 (randomly assign values to r0).
Set transition Matrix M and random surf vector d
3．If rn is converged (it does not change), the algorithm
finishes. The converged rn is the PageRank!!

40. Simple PageRank vs. complete PageRank
40
A
C D
B
Spider trap
0 1 10 100
A 1 0 0.01 0
B 0 0.333 0.015 0
C 0 0.333 0.961 1
D 0 0.333 0.015 0
Probability change in each iteration
0 1 10 100
A 1 0.05 0.102 0.101
B 0 0.316 0.129 0.128
C 0 0.316 0.639 0.642
D 0 0.316 0.129 0.128
Complete
PageRank
Simple
PageRank

41. What can PageRank provide us?
41
PageRank can evaluate
centrality of nodes in graph (network) data
Influential people Good papers to cite Popular webpage
Paper citation networks Web
PageRank PageRank PageRank

42. 2
42
Topic-sensitive PageRank
Improved PageRank to consider node’s topic

43. Issues of normal PageRank
43
Normal PageRank ignores what kinds of
topics each node is related to.
A
C D
B
E
■ Pages about medicine
■ Pages about cosmetic
F
G
Normal PageRank
1. Page C 0.282pt
2. A 0.174pt
3. F 0.133pt
4. D 0.132pt
5. B 0.093pt
6. E 0.092pt
7. G 0.092pt
Is Page C important from the viewpoint of medicine?

44. Which node is the most important about medicine?
44
■ Pages about medicine
■ Pages about cosmetic
A
C D
B
E F
G
Many pages link to C, but only one of them is about med.
A is linked by more pages about medicine than C

45. Issues of normal PageRank
45
Normal PageRank ignores what kinds of
topics each node is related to.
A
C D
B
E
■ Pages about medicine
■ Pages about cosmetic
F
G
Normal PageRank
1. Page C 0.282pt
2. A 0.174pt
3. F 0.133pt
4. D 0.132pt
5. B 0.093pt
6. E 0.092pt
7. G 0.092pt
Is Page C important from the viewpoint of medicine?
We sometimes want to find important
pages (nodes) about a certain topic.
If people often move to a page from
important pages about the topic, such
page should be important for the topic!

46. Assumption of Topic-sensitive PageRank
46
Normal PageRank
● People follow links in pages to visit other pages.
● They sometimes randomly visit pages without links.
Any kinds of
Topic-sensitive PageRank
● People follow links in pages to visit other pages.
● They sometimes randomly visit pages without links.
only a kind of

47. Algorithm of Topic-sensitive PageRank (1/2)
47
𝒓 𝒏 = 𝜶𝑴𝒓 𝒏1𝟏 + 1 − α 𝒅
Starting with n = 0, update rn with the below formula
0 1/2 0 0 0 0 1
0 0 0 1/3 0 0 0
1/4 0 0 1/3 1/2 1 0
1/4 1/2 0 0 0 0 0
1/4 0 0 0 0 0 0
0 0 0 1/3 1/2 0 0
1/4 0 0 0 0 0 0
A
C D
B
E F
G
1
1/4
1/4
1/4
1/4
1/2
1/21/3
1/3
1/3
1
1/2
1/2

48. Algorithm of Topic-sensitive PageRank (2/2)
48
𝒓 𝒏 = 𝜶𝑴𝒓 𝒏1𝟏 + 1 − α 𝒅
1/7
1/7
1/7
1/7
1/7
1/7
1/7
Normal
PageRank
A
C D
B
E F
G
1/4
1/4
1/4
0
0
0
1/4
Topic-sensitive
PageRank
Starting with n = 0, update rn with the below formula

49. Results of Topic-sensitive PageRank (TsPR)
49
● TsPR gives high scores to pages about target topics
■ Pages about medicine
■ Pages about cosmetic
A
C D
B
E F
G
Normal PageRank
1. C 0.282pt
2. A 0.174pt
3. F 0.133pt
4. D 0.132pt
5. B 0.093pt
6. E 0.092pt
7. G 0.092pt
Topic-sensitive PR
1. A 0.266pt
2. C 0.248pt
3. G 0.147pt
4. B 0.121pt
5. D 0.108pt
6. E 0.057pt
7. F 0.055pt
● Even if a page is not about target topics, if the page
is linked by important pages, TsPR gives high scores to it.

50. When do we use Topic-sensitive PageRank?
50
Finding important nodes in a graph
for target topics
1.
Finding important nodes for individual
users (personalizing PageRank)
2.
- For that, Give random surf values to only nodes for target topics
- If you know the nodes of a user to frequently visit, give random
surf values to only the nodes.
A
C D
B
E F
G
■ Pages which a user likes
𝒓 𝒏 = 𝜶𝑴𝒓 𝒏1𝟏 + 1 − α 𝒅
0
1/3
0
0
1/3
0
1/3