Clustering Semantically Similar Words

Clustering
Semantically
Similar Words
0.397
a
a’
DSW Camp & Jam
December 4th, 2016
Bayu Aldi Yansyah

- Understand step-by-step how to cluster words based on their
semantic similarity
- Understand how Deep learning model is applied to Natural
Language Processing
Our Goals
Overview

- You understand the basic of Natural Language Processing and
Machine Learning
- You are familiar with Artificial neural networks
I assume …
Overview

1. Introduction to Word Clustering
2. Introduction to Word Embedding
- Feed-forward Neural Net Language Model
- Continuous Bag-of-Words Model
- Continuous Skip-gram Model
3. Similarity metrics
- Cosine similarity
- Euclidean similarity
4. Clustering algorithm: Consensus clustering
Outline
Overview

1.
WORD CLUSTERING
INTRODUCTION
- Word clustering is a technique for partitioning sets of words into
subsets of semantically similar words
- Suppose we have set of words W = w$,w&, … , w( , n ∈ ℕ , our goal is
to find C = C$,C&, …, C. , k ∈ ℕ where
- w1 is a centroid of cluster C2
- similarity w1,w is a function to measure the similarity score
- and 𝑡 is a threshold value where if 𝑠𝑖𝑚𝑖𝑙𝑎𝑟𝑖𝑡𝑦 𝑤D , 𝑤 ≥ 𝑡 means that
𝑤D and 𝑤 is semantically similar.
- For 𝑤$ ∈ 𝐶G and 𝑤& ∈ 𝐶H apply that 𝑠𝑖𝑚𝑖𝑙𝑎𝑟𝑖𝑡𝑦 𝑤$, 𝑤& < 𝑡, so
𝐶J = 𝑤 ∀𝑤 ∈ 𝑊 where 𝑠𝑖𝑚𝑖𝑙𝑎𝑟𝑖𝑡𝑦 𝑤D, 𝑤 ≥ 𝑡}
𝐶G ∩ 𝐶H = ∅, ∀𝐶G,𝐶H ∈ 𝐶

1.
WORD CLUSTERING
INTRODUCTION
In order to perform word clustering, we need to:
1. Represent word as vector semantics, so we can compute their
similarity and dissimilarity score.
2. Find the w1 for each cluster.
3. Choose the similarity metric 𝑠𝑖𝑚𝑖𝑙𝑎𝑟𝑖𝑡𝑦 𝑤D, 𝑤 and the threshold
value 𝑡.

Semantic ≠ Synonym
“Words are similar semantically if they have the same thing, are
opposite of each other, used in the same way, used in the same
context and one is a type of another.” − Gomaa and Fahmy (2013)

2.
WORD EMBEDDING
INTRODUCTION
- Word embedding is a technique to represent a word as a vector.
- The result of word embedding frequently referred as “word vector”
or “distributed representation of words”.
- There are 3 main approaches to word embedding:
1. Neural Networks model based
2. Dimensionality reduction based
3. Probabilistic model based
- We focus on (1)
- The idea of these approaches are to learn vector representations of
words in an unsupervised manner.

2.
WORD EMBEDDING
INTRODUCTION
- Some Neural networks models that can learn representation of
words are:
1. Feed-forward Neural Net Language Model by
Bengio et al. (2003).
2. Continuous Bag-of-Words Model by Mikolov et al. (2013).
3. Continuous Skip-gram Model by Mikolov et al. (2013).
- We will compare these 3 models.
- Fun fact: the last two models is highly-inpired by no 1.
- Only Feed-forward Neural Net Language Model is considered as
deep learning model.

2.
WORD EMBEDDING
COMPARING NEURAL NETWORKS MODELS
- We will use notation from Collobert et al. (2011) to represent the
model. This help us to easily compare the models.
- Any feed-forward neural network with 𝐿 layers can be seen as a
composition of functions 𝑓T
U
(W), corresponding to each layer 𝑙:
- With parameter for each layer 𝑙:
- Usually each layer 𝑙 have weight 𝑊 and bias 𝑏, 𝜃U
= (𝑊U
,𝑏U
).
𝑓T W = 𝑓T
[
(𝑓T
[$
(… 𝑓T
$
(W)… ))
𝜃 = (𝜃$
,𝜃&
, …, 𝜃[
)

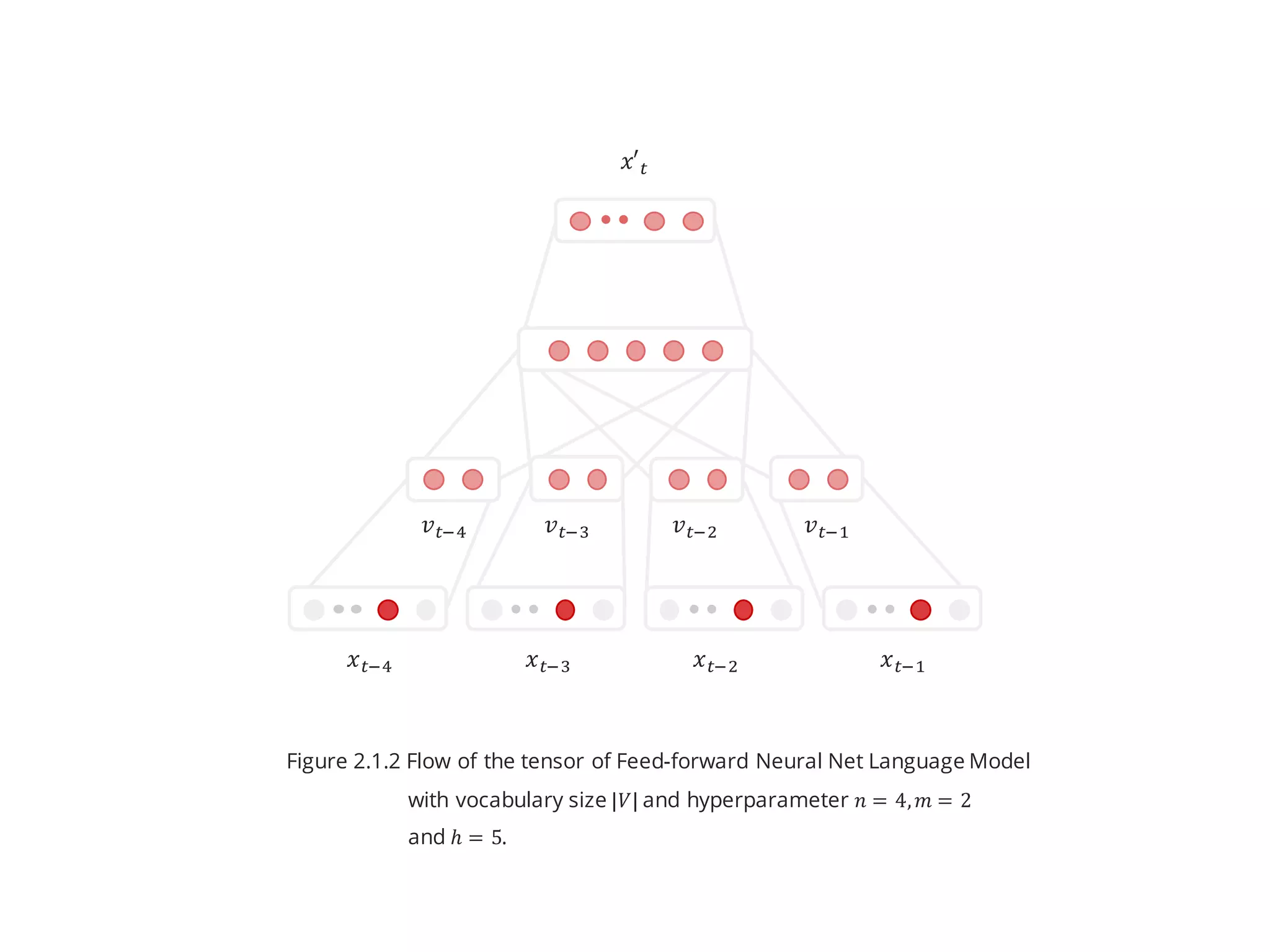
2.1.
FEED-FORWARD NEURAL NET LANGUAGE MODEL
Bengio et al. (2003)
- The training data is a sequence of words 𝑤$, 𝑤& , … , 𝑤] for 𝑤^ ∈ 𝑉
- The model is trying predict the next word 𝑤^ based on the previous
context (previous 𝑛 words: 𝑤^ $,𝑤^ &, … , 𝑤^ a). (Figure 2.1.1)
- The model is consist of 4 layers: Input layer, Projection layer, Hidden
layer(s) and output layer. (Figure 2.1.2)
- Known as NNLM
𝑤^
Keren Sale Stock bisa dirumah... ...
𝑤^ $𝑤^ &𝑤^ b𝑤^ c
Figure 2.1.1

2.1.
COMPOSITION OF FUNCTIONS: INPUT LAYER
- 𝑥^$,𝑥^&,… , 𝑥â is a 1-of-|𝑉| vector or one-hot-encoded vector of
𝑤^ $, 𝑤^&,… , 𝑤^ a
- 𝑛 is the number of previous words
- The input layer is just acting like placeholder here
𝑥′^ = 𝑓T 𝑥^$,… , 𝑥â
Output layer : 𝑓T
c
J
= 𝑥′^ = 𝜎 𝑊c]
𝑓T
b
J
+ 𝑏c
Hidden layer : 𝑓T
b
J
= tanh 𝑊b]
𝑓T
&
J
+ 𝑏b
Projection layer : 𝑓T
&
J
= 𝑊&]
𝑓T
$
J
Input layer for i-th example : 𝑓T
$
J = 𝑥^$, 𝑥^&, … , 𝑥â

2.1.
COMPOSITION OF FUNCTIONS: PROJECTION LAYER
- The idea of this layer is to project the |𝑉|-dimension vector to
smaller dimension.
- 𝑊&
is the |𝑉|× 𝑚 matrix, also known as embedding matrix, where
each row is a word vector
- Unlike hidden layer, there is no non-linearity here
- This layer also known as “The shared word features layer”
𝑥′^ = 𝑓T 𝑥^$,… , 𝑥^a
c
J
= 𝑥′^ = 𝜎 𝑊c]
𝑓T
b
J
+ 𝑏c
b
J
= tanh 𝑊b]
𝑓T
&
J
+ 𝑏b
&
J
= 𝑊&]
𝑓T
$
J
$
J = 𝑥^$, 𝑥^&, … , 𝑥^a

2.1.
COMPOSITION OF FUNCTIONS: HIDDEN LAYER
- 𝑊b
is the ℎ×𝑛𝑚 matrix where ℎ is the number of hidden units.
- 𝑏b
is a ℎ −dimensional vector.
- The activation function is hyperbolic tangent.
𝑥′^ = 𝑓T 𝑥^$,… , 𝑥^a
c
J
= 𝑥′^ = 𝜎 𝑊c]
𝑓T
b
J
+ 𝑏c
b
J
= tanh 𝑊b]
𝑓T
&
J
+ 𝑏b
&
J
= 𝑊&]
𝑓T
$
J
$
J = 𝑥^$, 𝑥^&, … , 𝑥^a

2.1.
COMPOSITION OF FUNCTIONS: OUPTUT LAYER
- 𝑊c
is the ℎ×|𝑉| matrix.
- 𝑏c
is a |𝑉|-dimensional vector.
- The activation function is softmax.
- 𝑥′^ is a |𝑉|-dimensional vector.
𝑥′^ = 𝑓T 𝑥^$,… , 𝑥^a
c
J
= 𝑥′^ = 𝜎 𝑊c]
𝑓T
b
J
+ 𝑏c
b
J
= tanh 𝑊b]
𝑓T
&
J
+ 𝑏b
&
J
= 𝑊&]
𝑓T
$
J
$
J = 𝑥^$, 𝑥^&, … , 𝑥^a

2.1.
LOSS FUNCTION
- Where 𝑁 is the number of training data
- The goal is to maximize this loss function.
- The neural networks are trained using stochastic gradient ascent.
𝐿 =
1
𝑁
n log 𝑓T 𝑥^$, …, 𝑥^a ; 𝜃 J
r
Js$

Figure 2.1.2 Flow of the tensor of Feed-forward Neural Net Language Model
with vocabulary size |𝑉| and hyperparameter 𝑛 = 4, 𝑚 = 2
and ℎ = 5.
𝑥^$𝑥^&𝑥^b𝑥^c
𝑣^$𝑣^&𝑣^b𝑣^c
𝑥′^

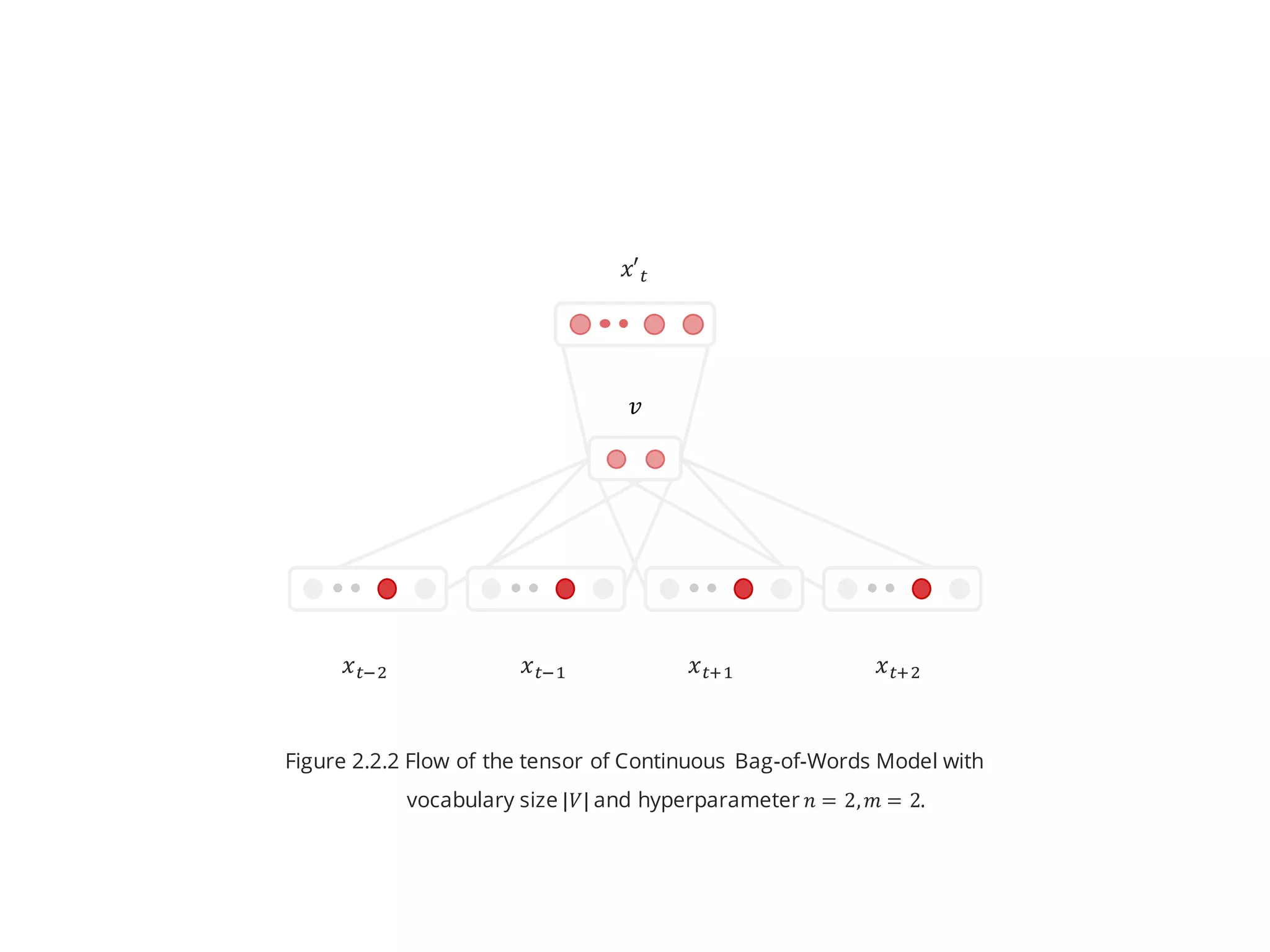
2.2.
CONTINUOUS BAG-OF-WORDS MODEL
Mikolov et al. (2013)
- The model is trying predict the word 𝑤^ based on the surrounding
context (𝑛 words from left: 𝑤^$,𝑤^ & and 𝑛 words from the right:
𝑤^ $, 𝑤^&). (Figure 2.2.1)
- There are no hidden layer in this model.
- Projection layer is averaged across input words.
𝑤^ x&
Keren Sale bisa bayar dirumah... ...
𝑤^ x$𝑤^𝑤^ $𝑤^ &
Figure 2.2.1

2.2.
- 𝑥^y is a 1-of-|𝑉| vector or one-hot-encoded vector of 𝑤^y.
- 𝑛 is the number of words on the left and the right.
𝑥′^ = 𝑓T 𝑥^a, … , 𝑥^$,𝑥^x$, …, 𝑥^xa
b
J
= 𝑥′^ = 𝜎 𝑊b]
𝑓T
&
J
+ 𝑏b
&
J
= 𝑣 =
1
2𝑛
n 𝑊&]
𝑓T
$
(𝑗) J
a{y{a,y|}
y
$
(𝑗) J = 𝑥^y, −𝑛 ≤ 𝑗 ≤ 𝑛, 𝑗 ≠ 0

2.2.
- The difference from previous model is this model project all the
inputs to one 𝑚-dimensional vector 𝑣.
- 𝑊&
each row is a word vector.
𝑥′^ = 𝑓T 𝑥^a, … , 𝑥^$,𝑥^x$, …, 𝑥^xa
b
J
= 𝑥′^ = 𝜎 𝑊b]
𝑓T
&
J
+ 𝑏b
&
J
= 𝑣 =
1
2𝑛
n 𝑊&]
𝑓T
$
(𝑗) J
a{y{a,y|}
y
$
(𝑗) J = 𝑥^y, −𝑛 ≤ 𝑗 ≤ 𝑛, 𝑗 ≠ 0

2.2.
COMPOSITION OF FUNCTIONS: OUPTUT LAYER
- 𝑊b
is the m×|𝑉| matrix.
- 𝑏b
is a |𝑉|-dimensional vector.
- 𝑥′^ is a |𝑉|-dimensional vector.
𝑥′^ = 𝑓T 𝑥^a, … , 𝑥^$,𝑥^x$, …, 𝑥^xa
b
J
= 𝑥′^ = 𝜎 𝑊b]
𝑓T
&
J
+ 𝑏b
&
J
= 𝑣 =
1
2𝑛
n 𝑊&]
𝑓T
$
(𝑗) J
a{y{a,y|}
y
$
(𝑗) J = 𝑥^y, −𝑛 ≤ 𝑗 ≤ 𝑛, 𝑗 ≠ 0

2.2.
CONTINOUS BAG-OF-WORDS MODEL
LOSS FUNCTION
𝐿 =
1
𝑁
n log 𝑓T 𝑥^a , … , 𝑥^$, 𝑥^x$,… , 𝑥^xa J
r
Js$

𝑥^x&𝑥^x$𝑥^$𝑥^&
𝑥′^
𝑣
Figure 2.2.2 Flow of the tensor of Continuous Bag-of-Words Model with
vocabulary size |𝑉| and hyperparameter 𝑛 = 2, 𝑚 = 2.

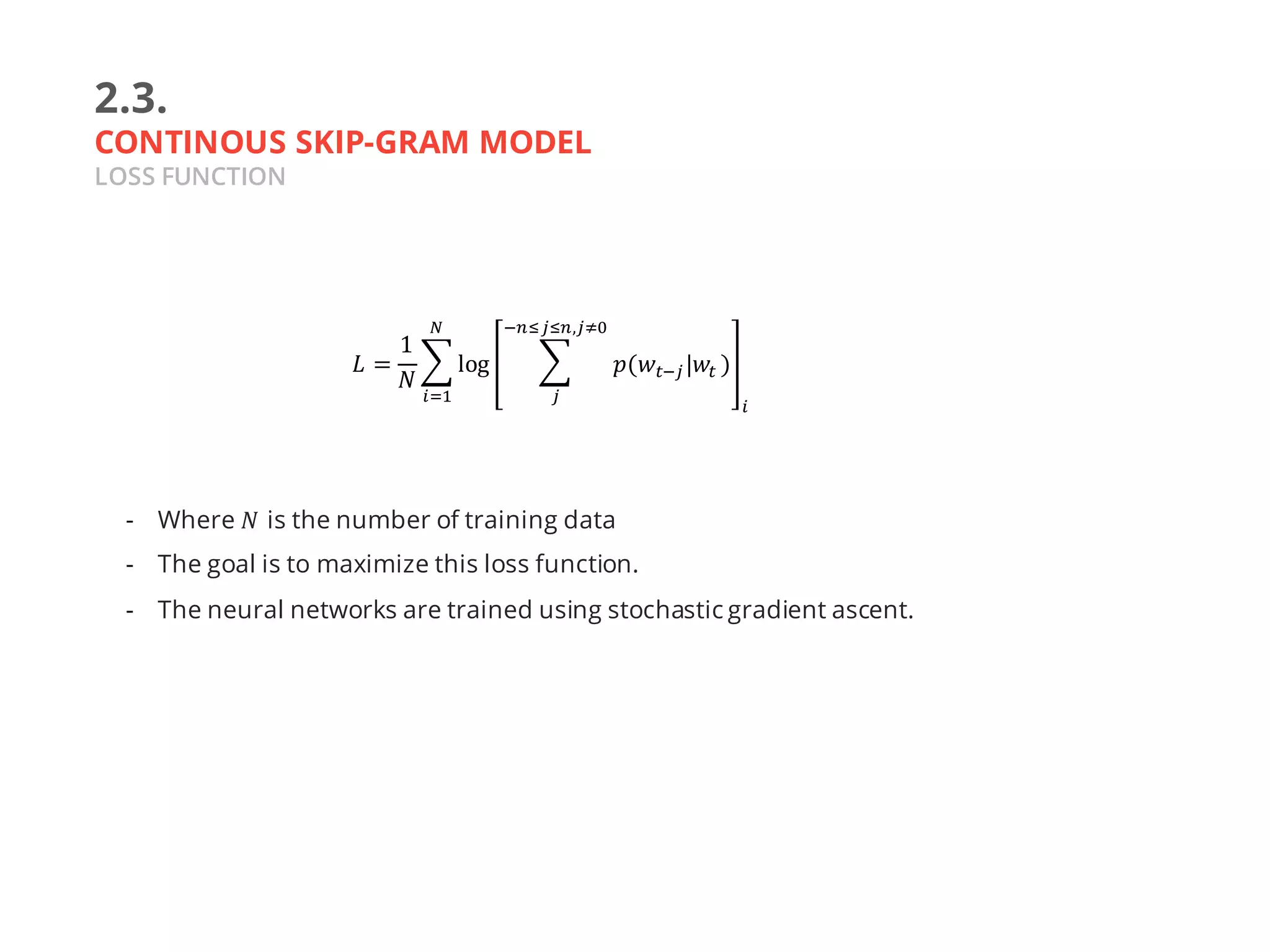
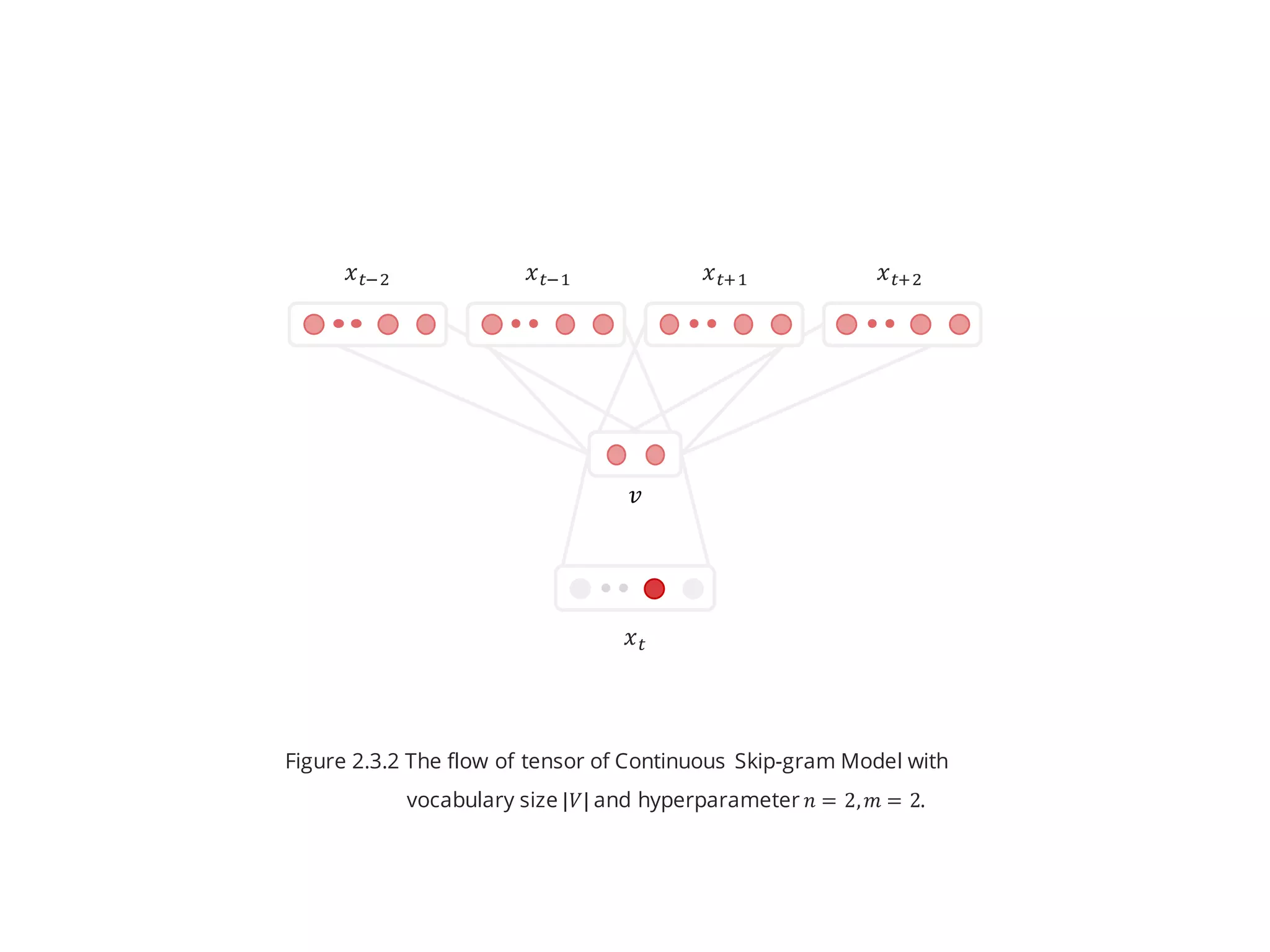
2.3.
CONTINUOUS SKIP-GRAM MODEL
Mikolov et al. (2013)
- The model is trying predict the surrounding context (𝑛 words from
left: 𝑤^$,𝑤^ & and 𝑛 words from the right: 𝑤^ $,𝑤^ &) based on the
word 𝑤^ . (Figure 2.3.1)
𝑤^ x&
Keren bisa... ...
𝑤^ x$𝑤^𝑤^ $𝑤^ &
Figure 2.3.1

2.3.
- 𝑥^ is a 1-of-|𝑉| vector or one-hot-encoded vector of 𝑤^ .
𝑋′ = 𝑓T 𝑥^
b
J
= 𝑋′ = 𝜎 𝑊b]
𝑓T
&
J
+ 𝑏b
&
J
= 𝑊&]
𝑓T
$
J
$
J = 𝑥^

2.3.
- 𝑊&
each row is a word vector.
- Same as Continuous Bag-of-Words model
b
J
= 𝑋′ = 𝜎 𝑊b]
𝑓T
&
J
+ 𝑏b
&
J
= 𝑊&]
𝑓T
$
J
$
J = 𝑥^

2.3.
COMPOSITION OF FUNCTIONS: OUTPUT LAYER
- 𝑊b
is the m×2𝑛|𝑉| matrix.
- 𝑏b
is a 2n|𝑉|-dimensional vector.
- 𝑋‚
is a 2n|𝑉|-dimensional vector can be written as
b
J
= 𝑋′ = 𝜎 𝑊b]
𝑓T
&
J
+ 𝑏b
&
J
= 𝑊&]
𝑓T
$
J
$
J = 𝑥^
𝑋‚
= (𝑝(𝑤^a |𝑤^ ), … , 𝑝(𝑤^$ |𝑤^ ), 𝑝(𝑤^x$|𝑤^ ),… , 𝑝(𝑤^xa |𝑤^ ))

2.3.
CONTINOUS SKIP-GRAM MODEL
LOSS FUNCTION
𝐿 =
1
𝑁
n log n 𝑝(𝑤^y|𝑤^ )
a{y{a,y|}
y
J
r
Js$

𝑥^x&𝑥^x$𝑥^$𝑥^&
𝑥^
𝑣
Figure 2.3.2 The flow of tensor of Continuous Skip-gram Model with
vocabulary size |𝑉| and hyperparameter 𝑛 = 2, 𝑚 = 2.

3.
SIMILARITY METRICS
INTRODUCTION
- Recall 𝑠𝑖𝑚𝑖𝑙𝑎𝑟𝑖𝑡𝑦 𝑤D , 𝑤 ≥ 𝑡
- Similarity metrics of words: Character-Based Similarity Measures
and Term-based Similarity Measures. (Gomaa and Fahmy 2013)
- We focus on Term-based Similarity Measures

3.
SIMILARITY METRICS
INTRODUCTION
- Recall 𝑠𝑖𝑚𝑖𝑙𝑎𝑟𝑖𝑡𝑦 𝑤D , 𝑤 ≥ 𝑡
- Similarity metrics of words: Character-Based Similarity Measures
and Term-based Similarity Measures. (Gomaa and Fahmy 2013)
- We focus on Term-based Similarity Measures: Cosine & Euclidean.

3.1.
SIMILARITY METRICS
COSINE
- Where 𝑣J is our word vector
- Range value: −1 ≤ 𝑠𝑖𝑚𝑖𝑙𝑎𝑟𝑖𝑡𝑦 𝑣$,𝑣& ≤ 1
- Recommended threshold value : 𝑡 ≥ 0.5
𝑠𝑖𝑚𝑖𝑙𝑎𝑟𝑖𝑡𝑦 𝑣$, 𝑣& =
𝑣$ W 𝑣&
𝑣$ 𝑣&

3.2.
SIMILARITY METRICS
EUCLIDEAN
- Where 𝑣J is our word vector
- Range value: 0 ≤ 𝑠𝑖𝑚𝑖𝑙𝑎𝑟𝑖𝑡𝑦 𝑣$, 𝑣& ≤ 1
- Recommended threshold value : 𝑡 ≥ 0.75
𝑠𝑖𝑚𝑖𝑙𝑎𝑟𝑖𝑡𝑦 𝑣$,𝑣& =
1
1 − 𝑑𝑖𝑠𝑡𝑎𝑛𝑐𝑒(𝑣$,𝑣&)
𝑑𝑖𝑠𝑡𝑎𝑛𝑐𝑒 𝑣$,𝑣& = n(𝑣$J − 𝑣&J)&
a
Js$

4.
CONSENSUS CLUSTERING
INTRODUCTION
- The basic idea here is we want to find the 𝑤D based on the
consensus
- There are 3 approaches for Consensus clustering: Iterative Voting
Consensus, Iterative Probabilistic Voting Consensus and Iterative
Pairwise Consensus. (Nguyen and Caruana 2007)
- We use slightly modified version of Iterative Voting Consensus

4.1.
CONSENSUS CLUSTERING
THE ALGORITHM
Figure 4.1.1 Iterative Voting Consensus with slightly modification

5.
CASE STUDY
OR DEMO
- Let’s do this

thanks! | @bayualsyah
Notes available here: https://github.com/pyk/talks

Clustering Semantically Similar Words

More Related Content

What's hot

Viewers also liked

Similar to Clustering Semantically Similar Words

More from Bayu Aldi Yansyah

Recently uploaded

Clustering Semantically Similar Words