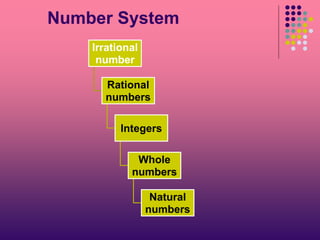
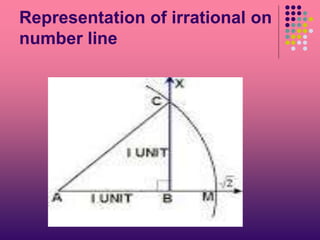
Rational numbers are numbers that can be represented as fractions p/q where p and q are integers and q is not equal to 0, such as 2/5 or 4/7. Irrational numbers are numbers that cannot be represented as fractions, such as √2 or √3, and their decimal representations are non-terminating and non-repeating. Real numbers include both rational and irrational numbers and can all be represented as unique points on a number line, with rational numbers having either terminating or non-terminating repeating decimals and irrational numbers having non-terminating, non-repeating decimals.

1. Rational and
Irrational number
Rational numbers are in the
form of p/q where p and
q both are integers and q is not
equal to 0
Eg 2/5 , 4/7 ,7/20

2. Number System
Irrational
number
Rational
numbers
Integers
Whole
numbers
Natural
numbers

3.  Real numbers
The collection of irrational and rational numbers
are called as real numbers.
Every real number can be represented by a
unique point on a number line.
Two German Mathematician Cantor and
Dedekind showed that corresponding to
every real number there is a point on the real
number line.

4. Terminating and non terminating
decimals
 The decimal expansion of a rational
number is either terminating or non
terminating recurring.
 Irrational numbers are non
terminating and non repeating.

5. Examples of irrational
numbers
 √2 , √14
 √24 , √10
 √12, √7
All the numbers can be represented on a
number line

6.  If the denominator in the rational number in the
lowest form is the multiple of 2 or 5 or both then
the number is terminating
 Eg 3/ 128
The denominator can be represented in the form
of 27 ,hence the number is terminating.

7. Rationalising the denominator
 If we have a number 1/√7
We can rationalize the denominator by
multiplying the number by √7
We get 1/√7 x √7/ √7
√7/ 7

8.  Every point on a number line represents a
real number.
 We can represent √2 , √3, √5 on a number
line

9. Representation of irrational on
number line

10. Conclusion
 Rational numbers are either terminating or
non terminating repeating decimals
 Irrational numbers are non terminating non
repeating decimals.
 Every real numbers can be represented on a
number line
 Every point on a number line represents a
real numbers.