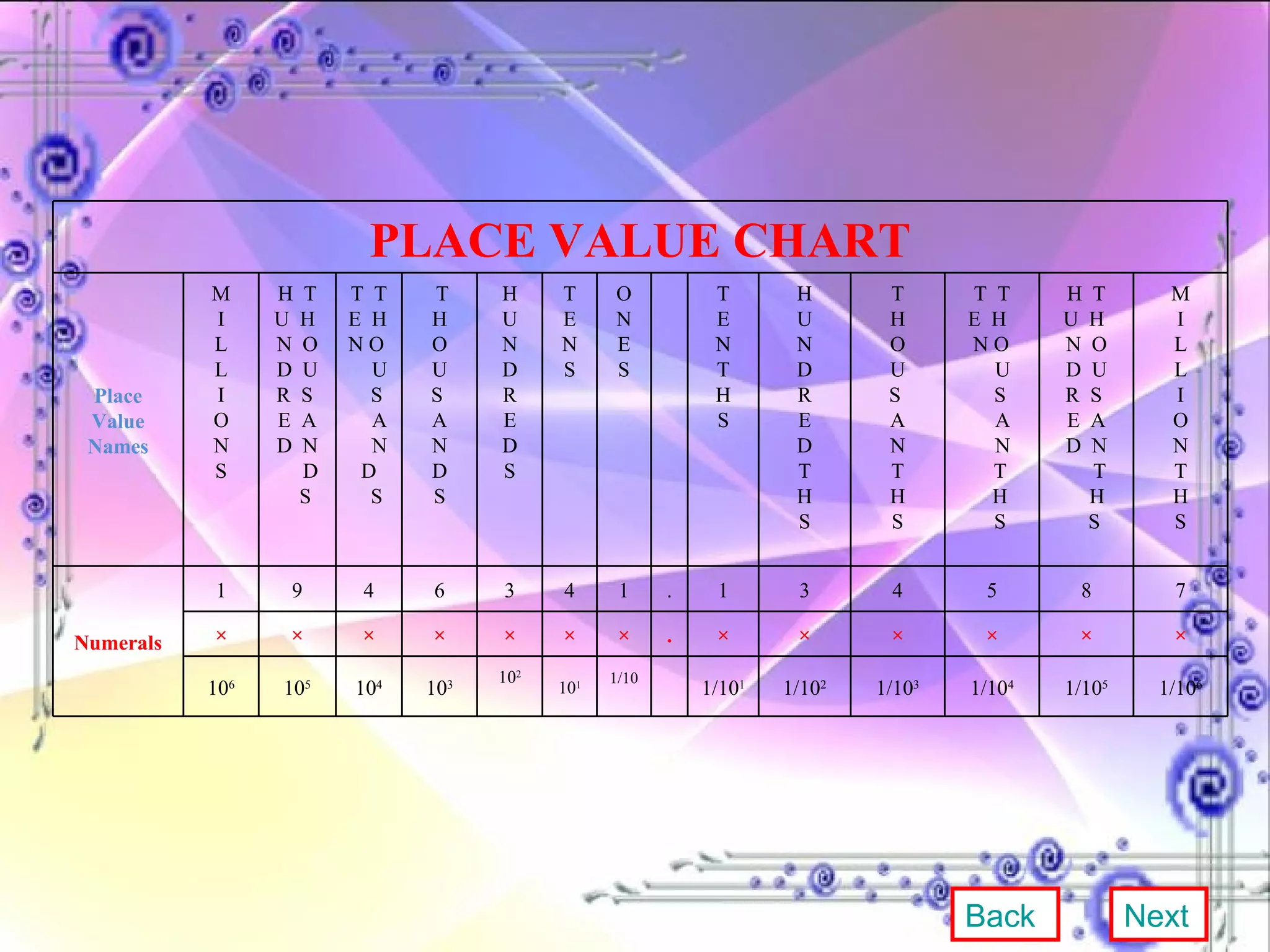
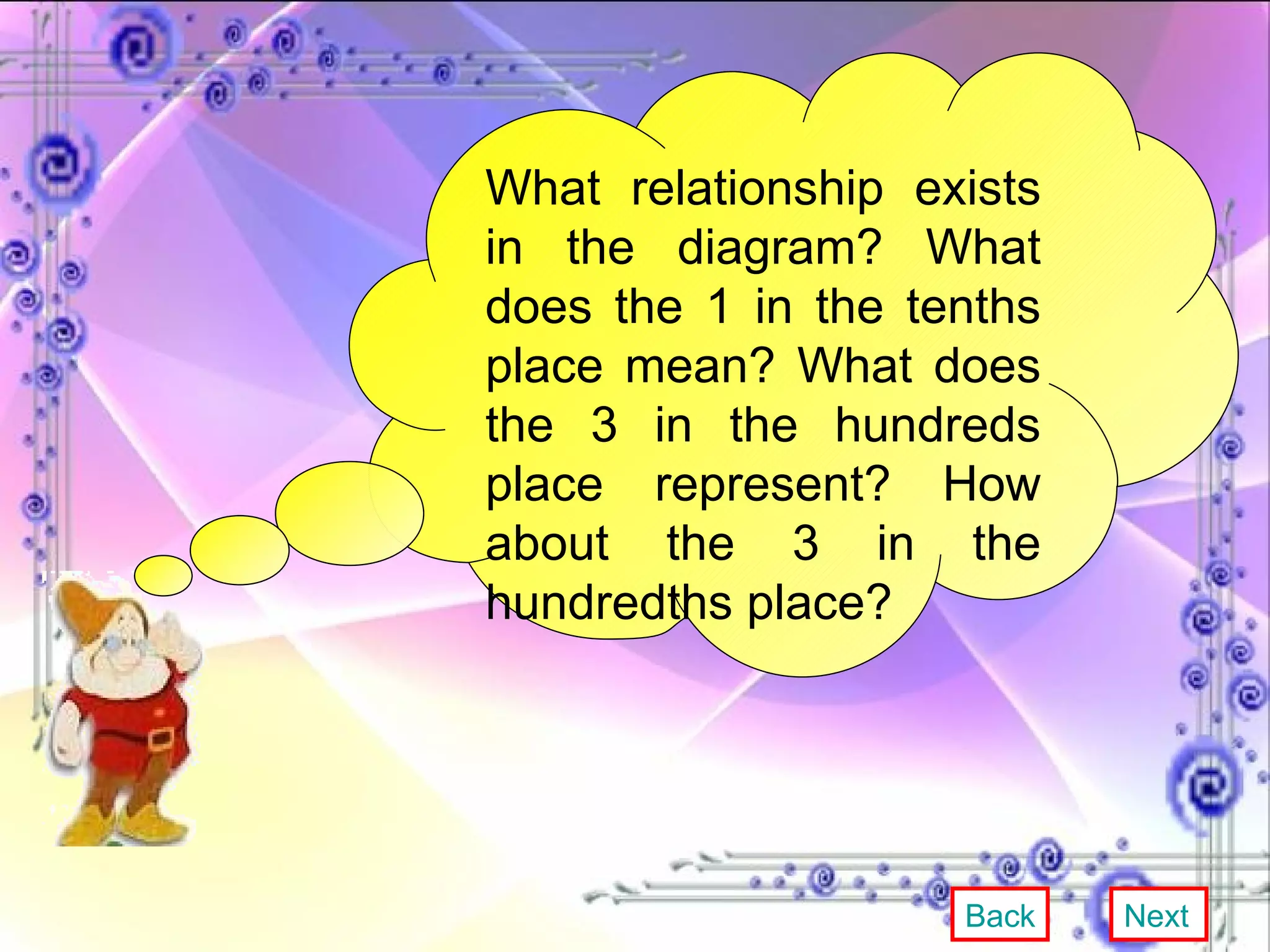
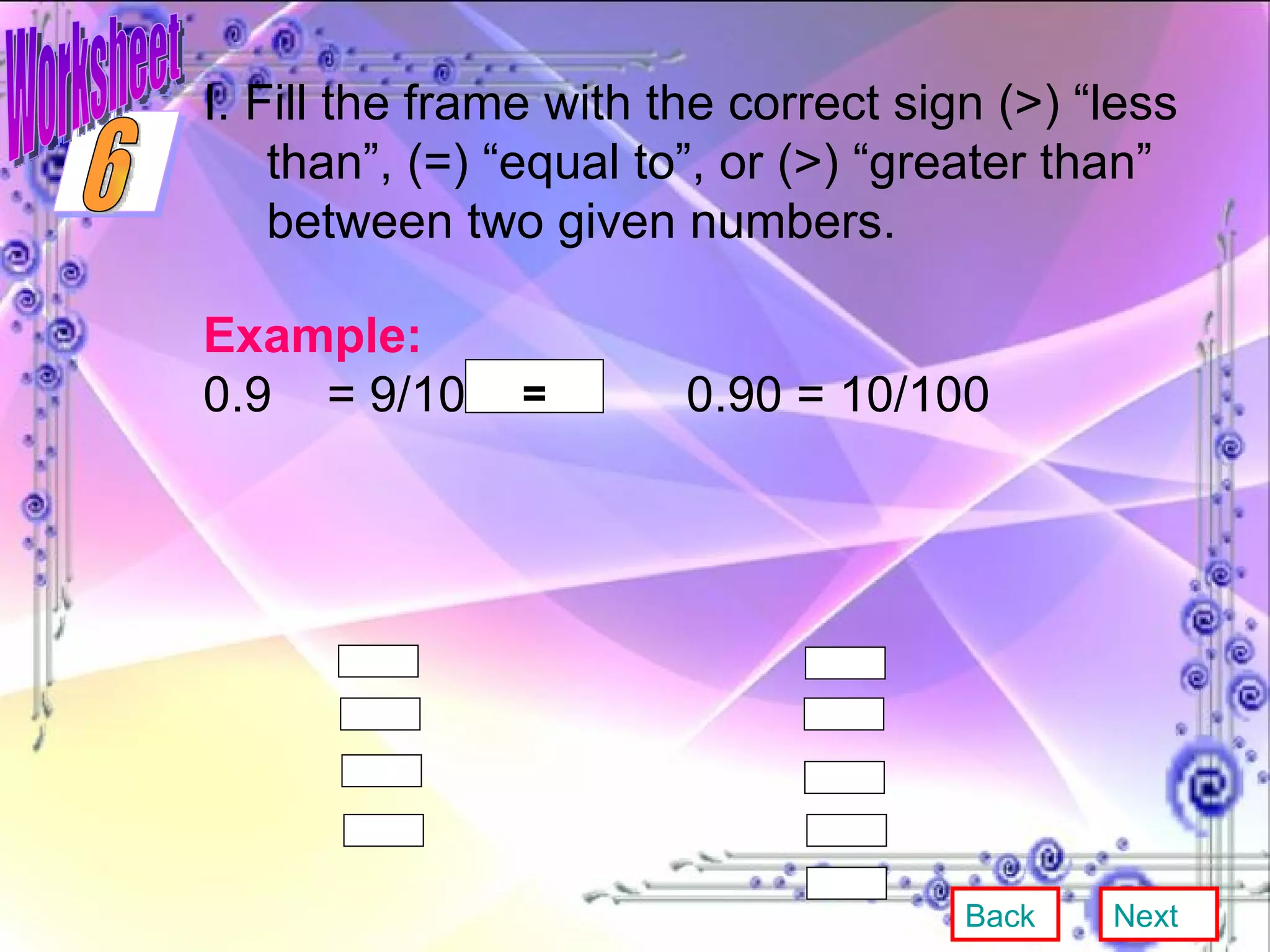
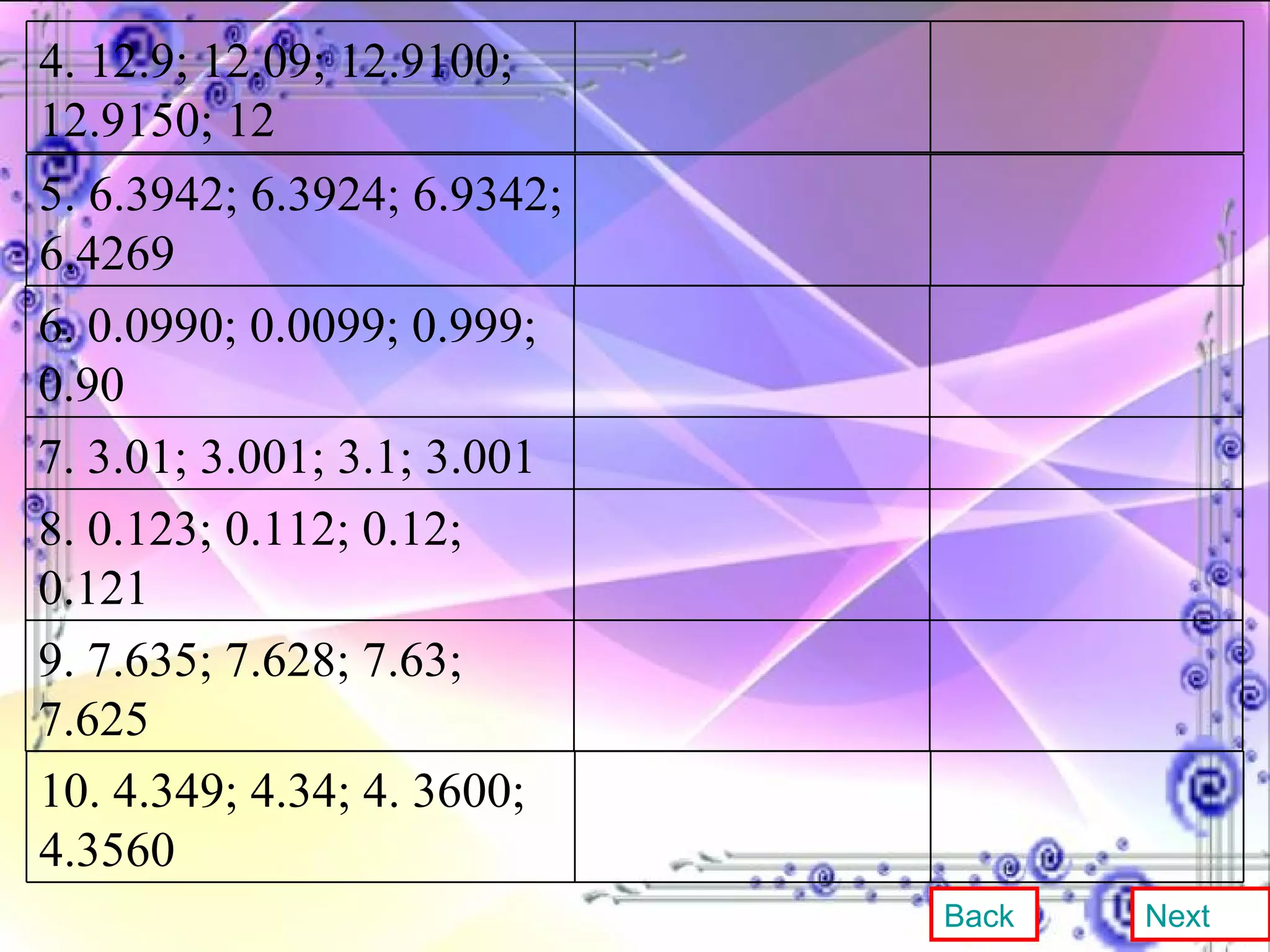
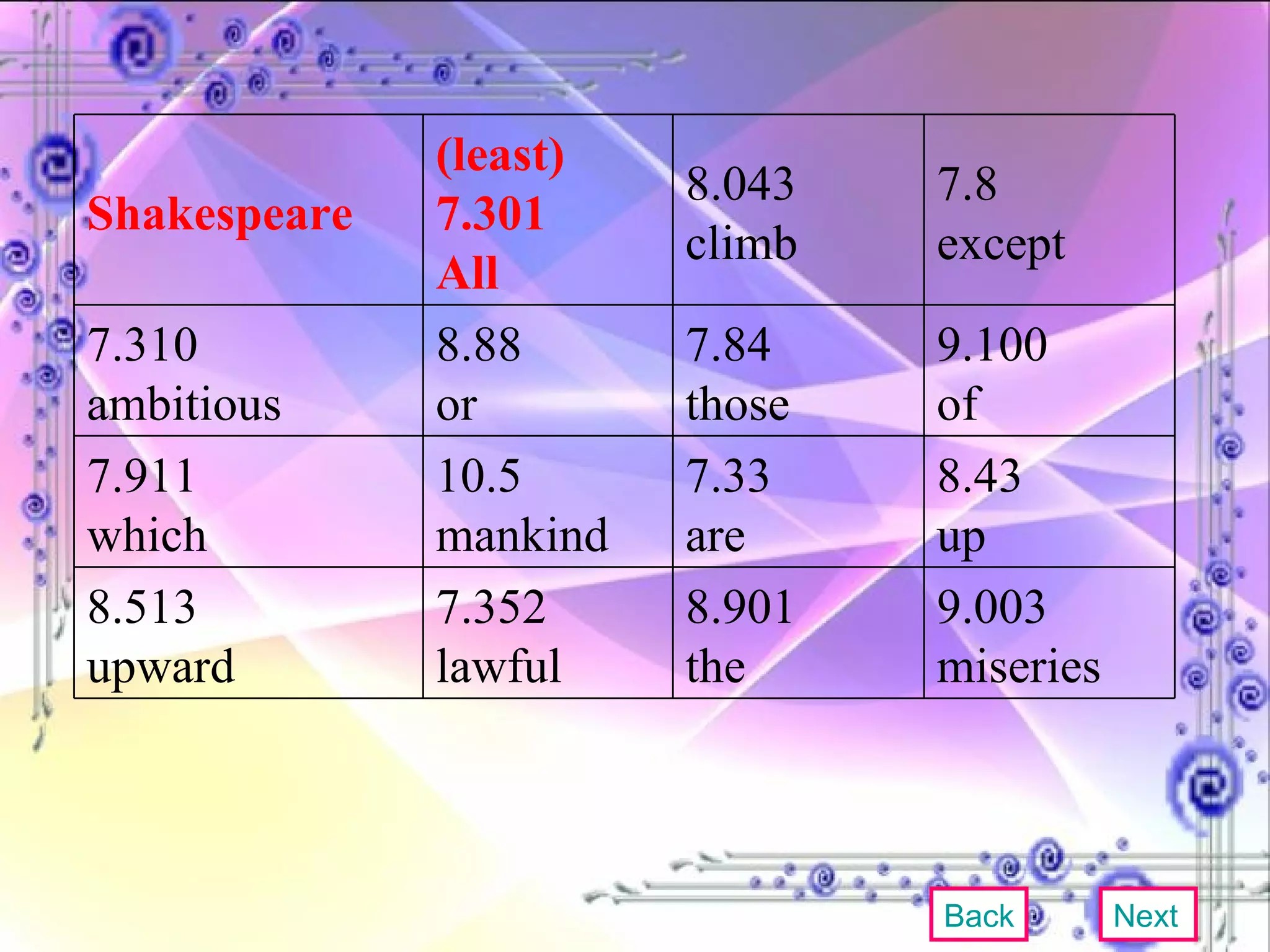
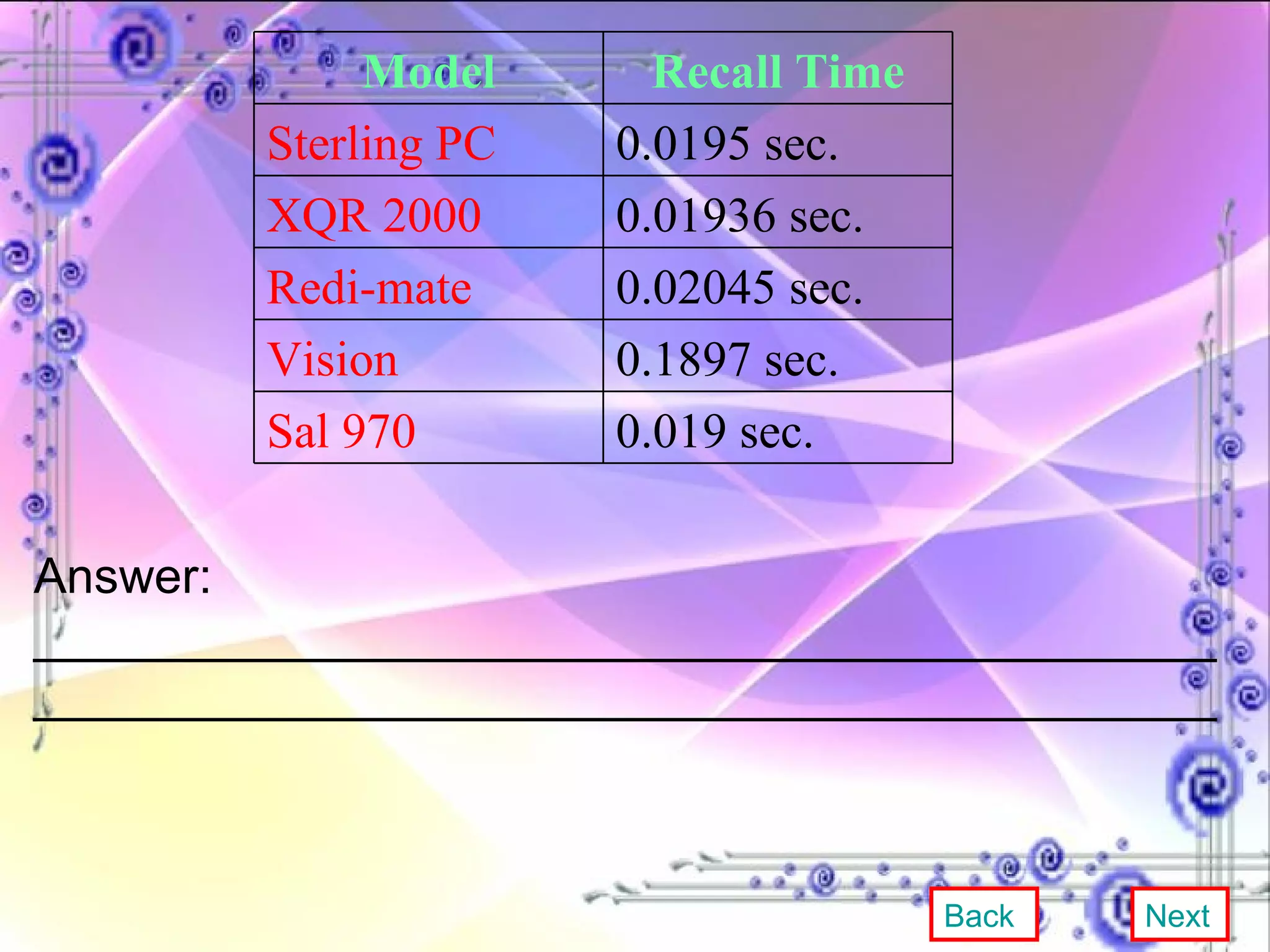
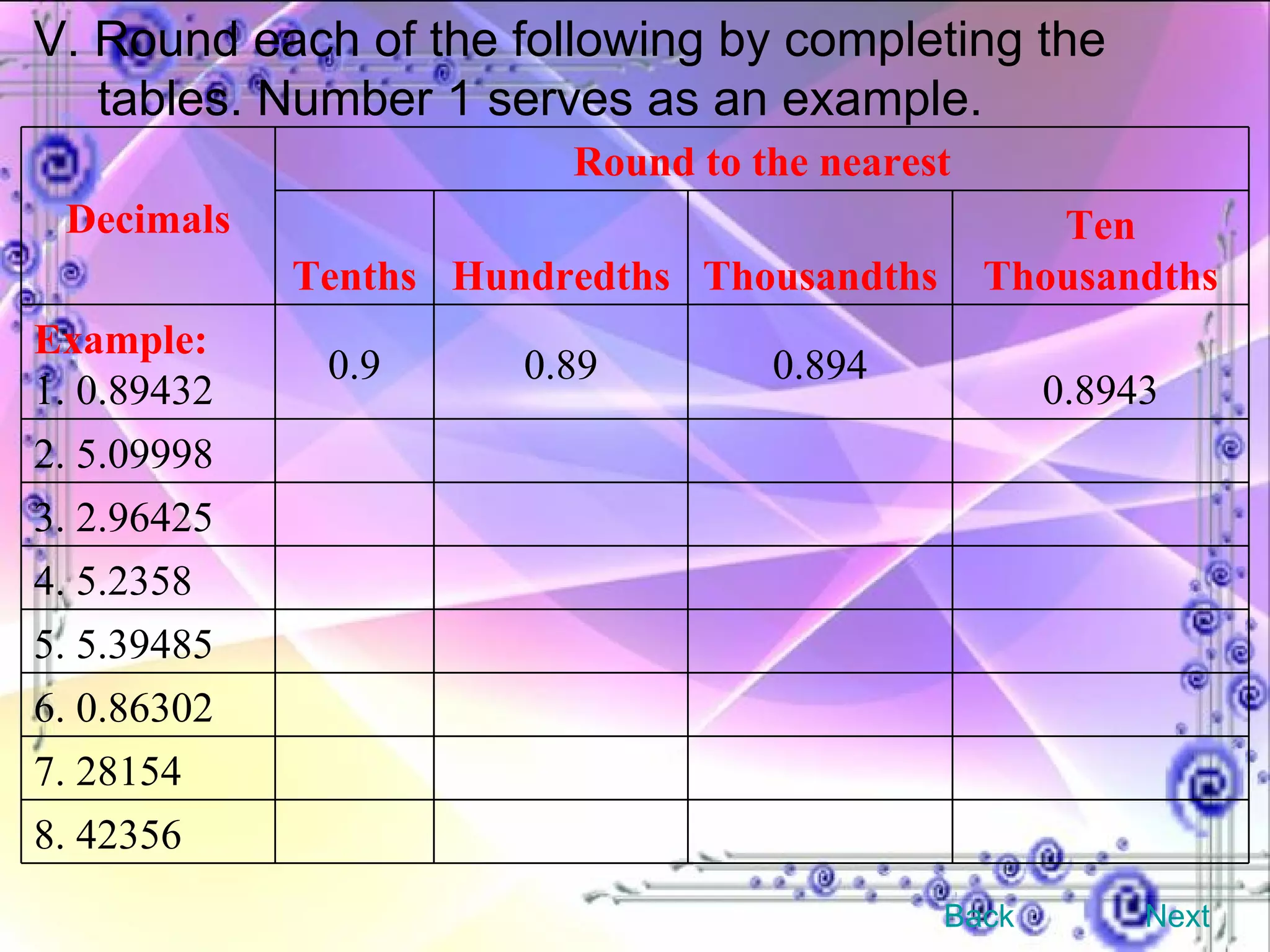
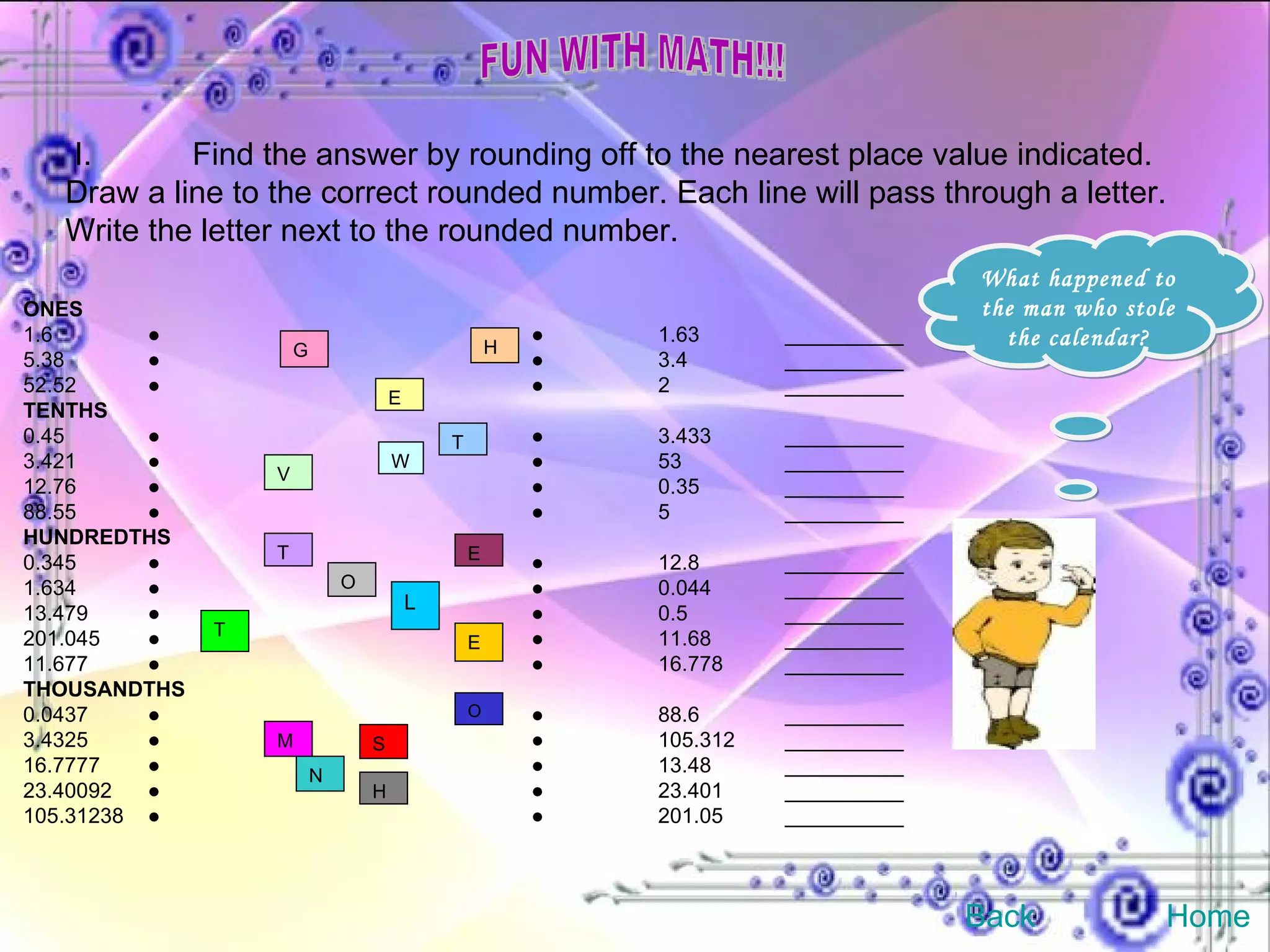
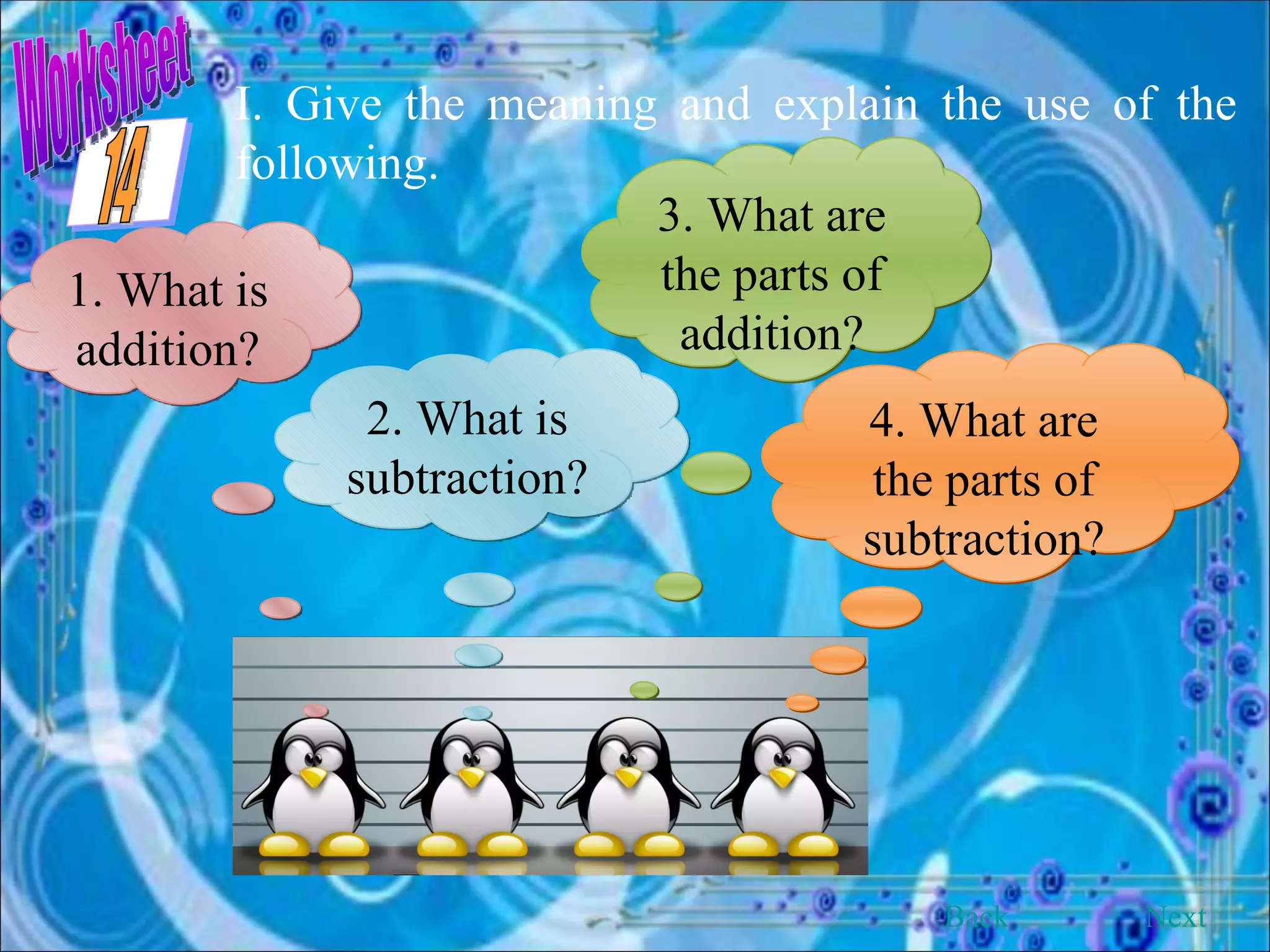
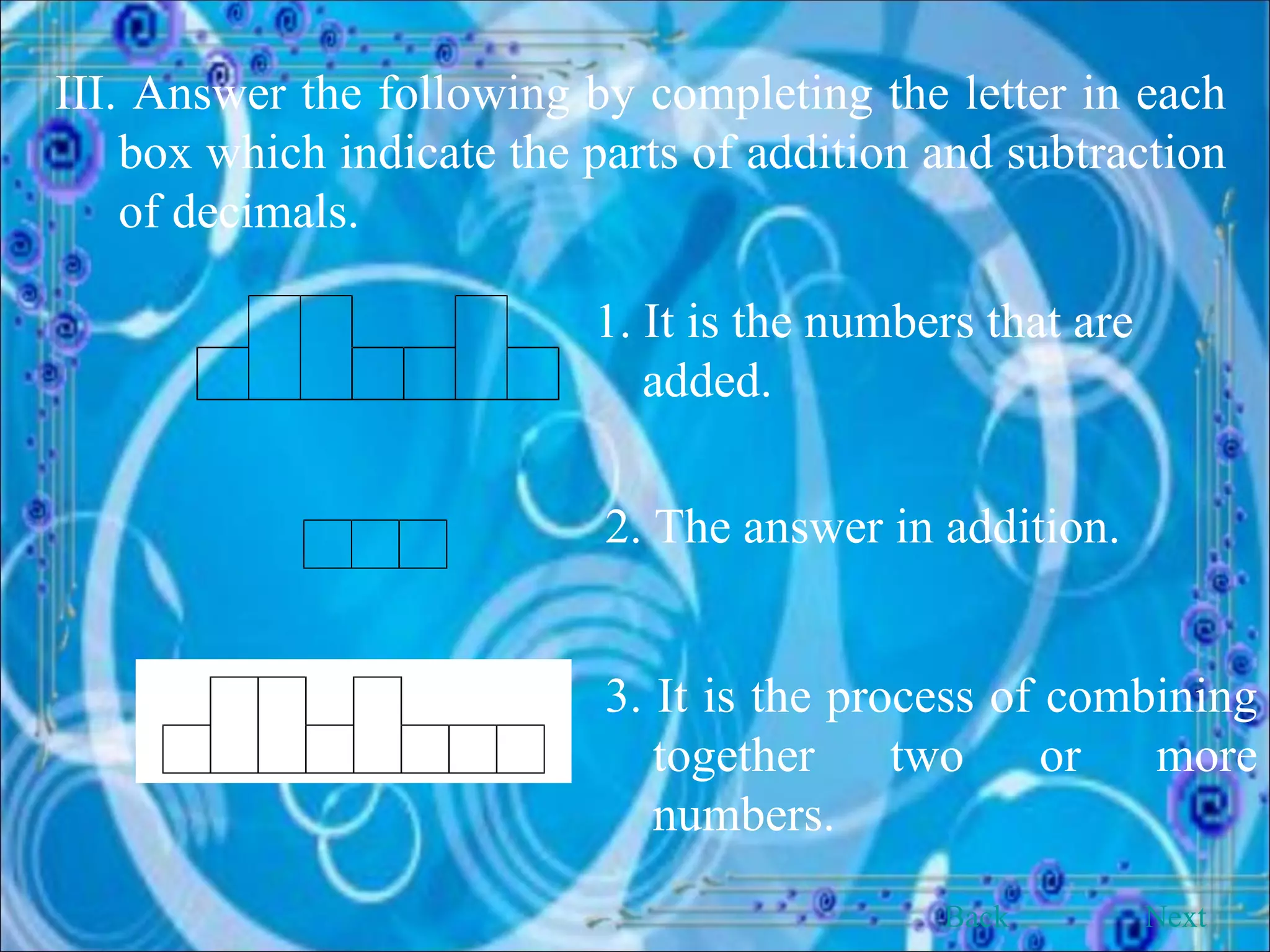
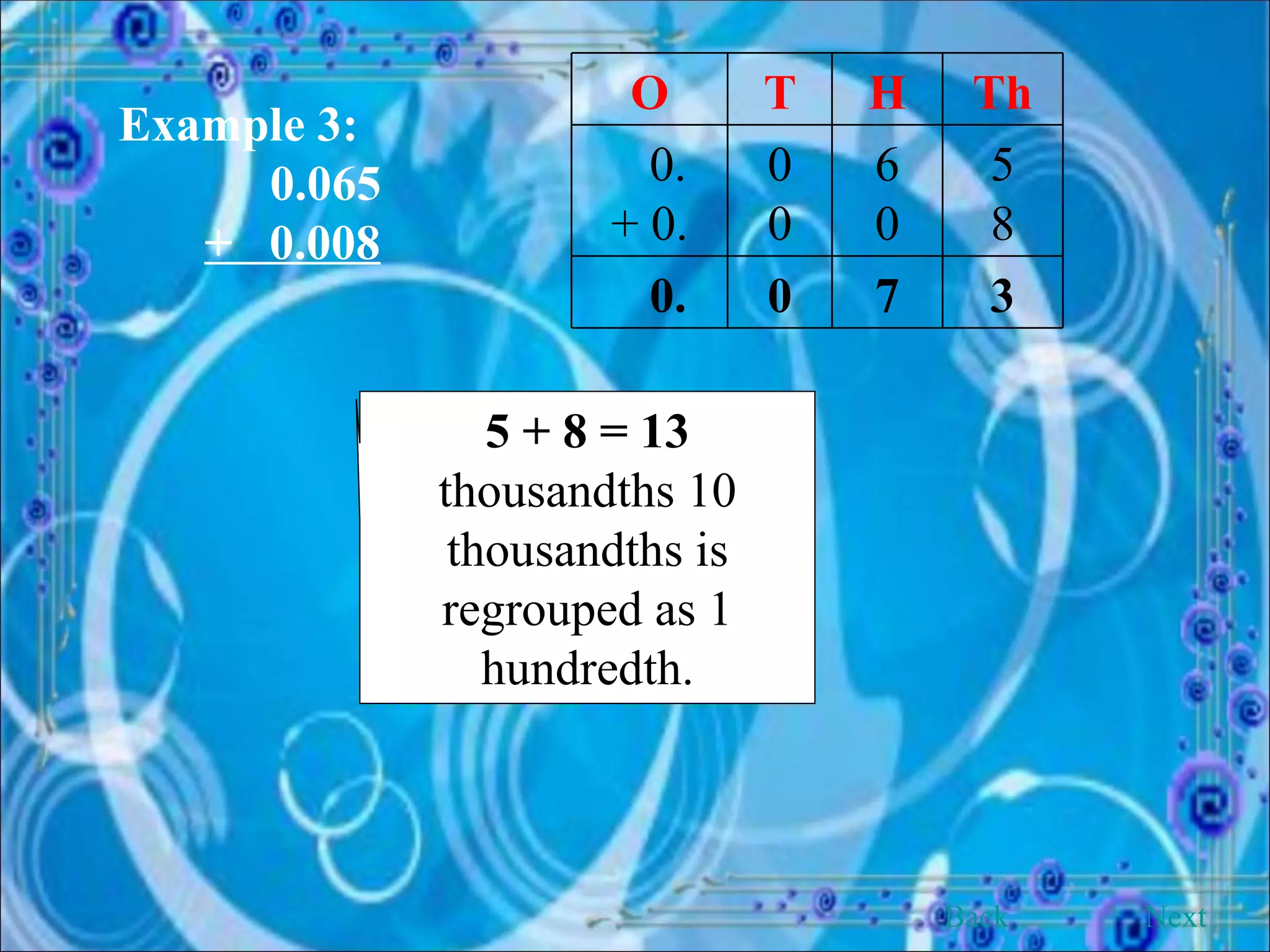
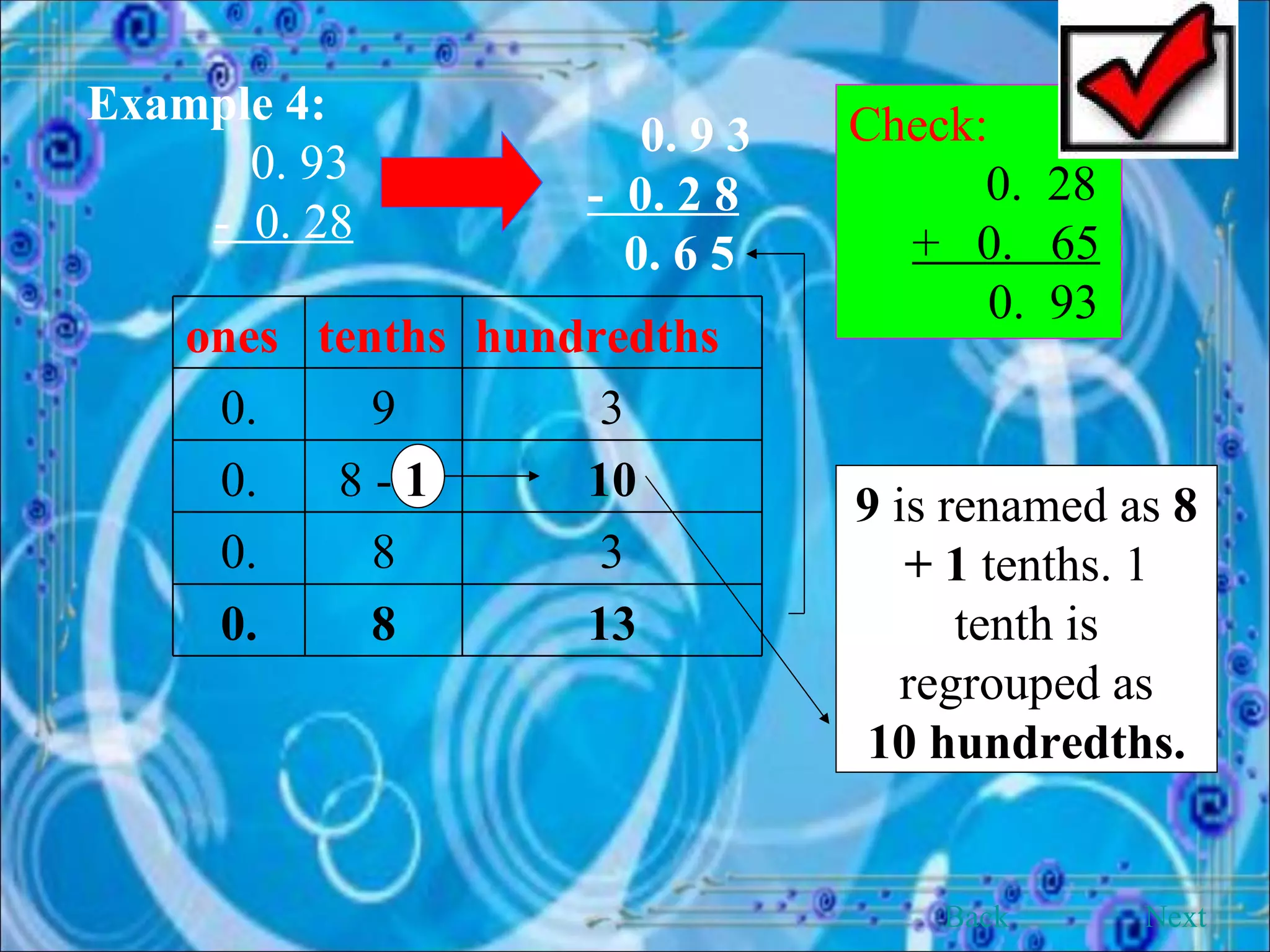
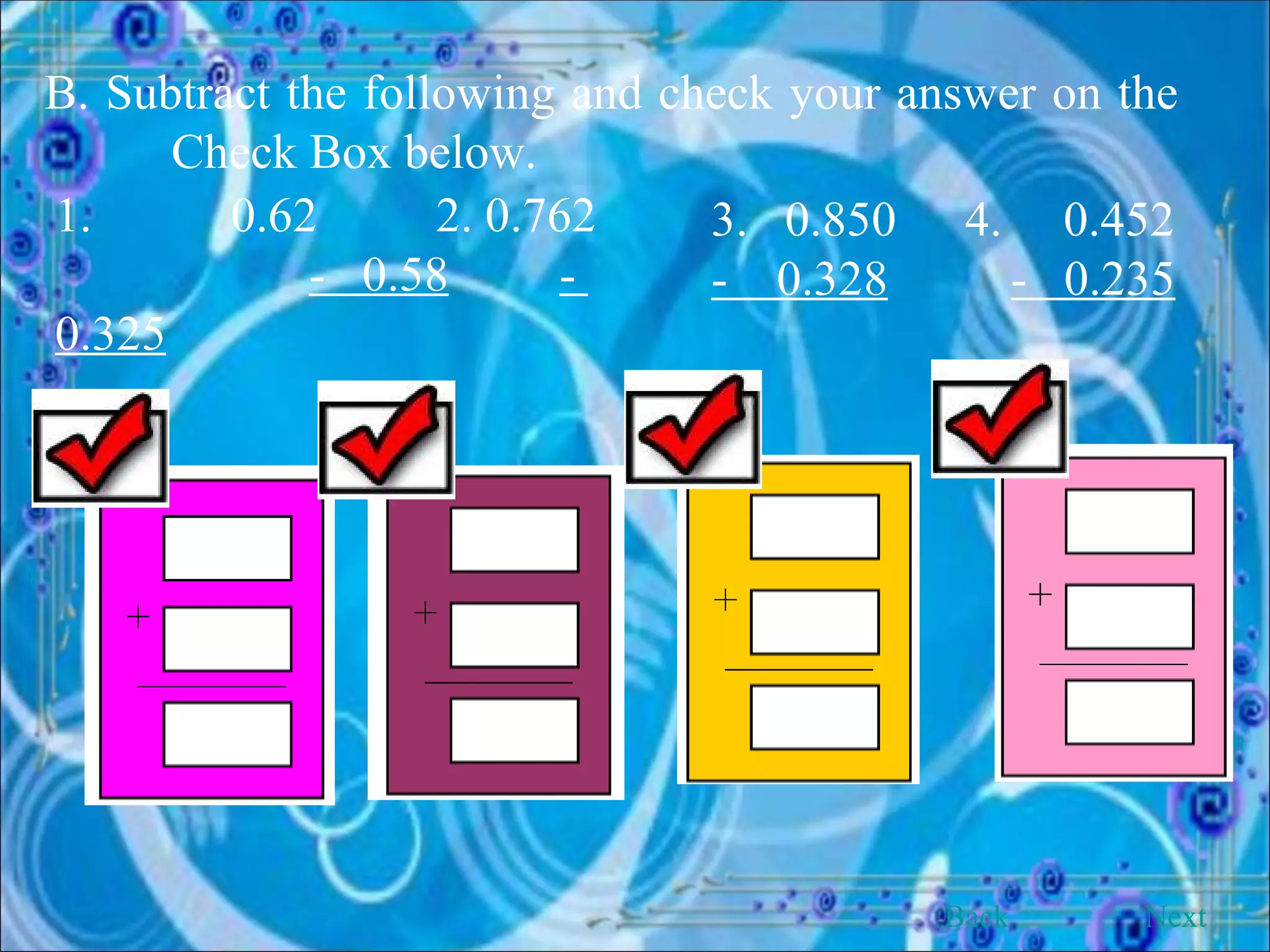
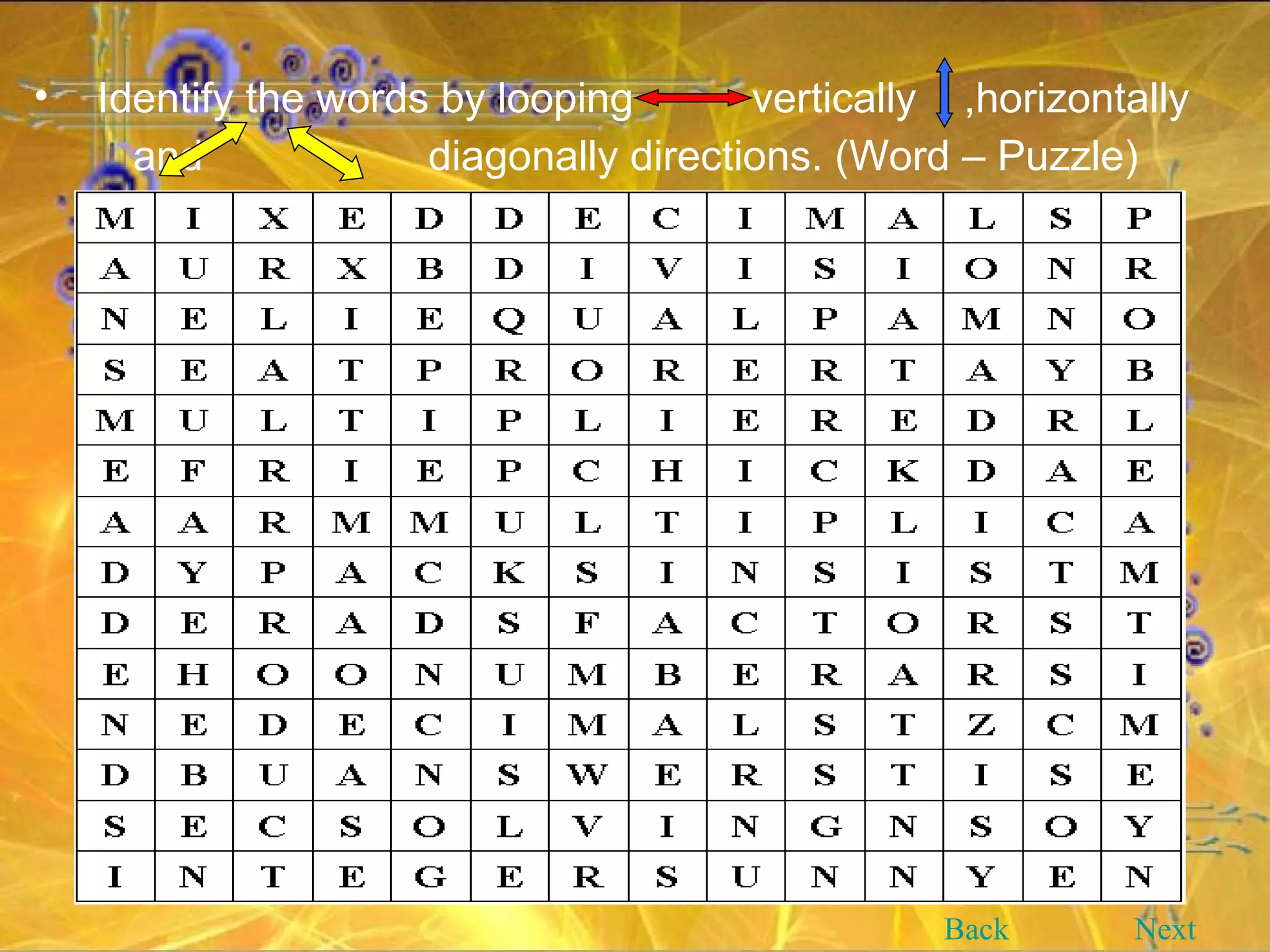
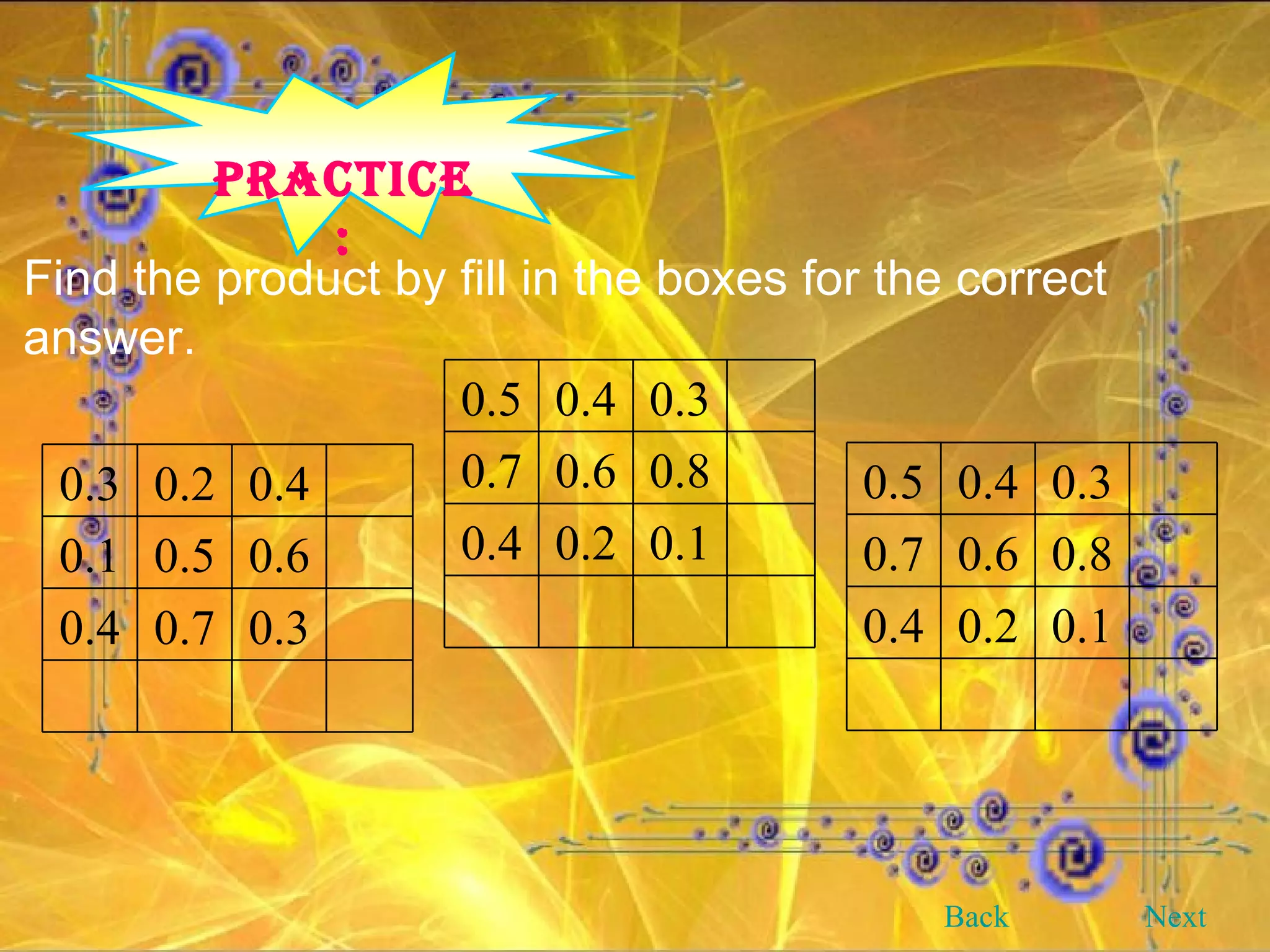
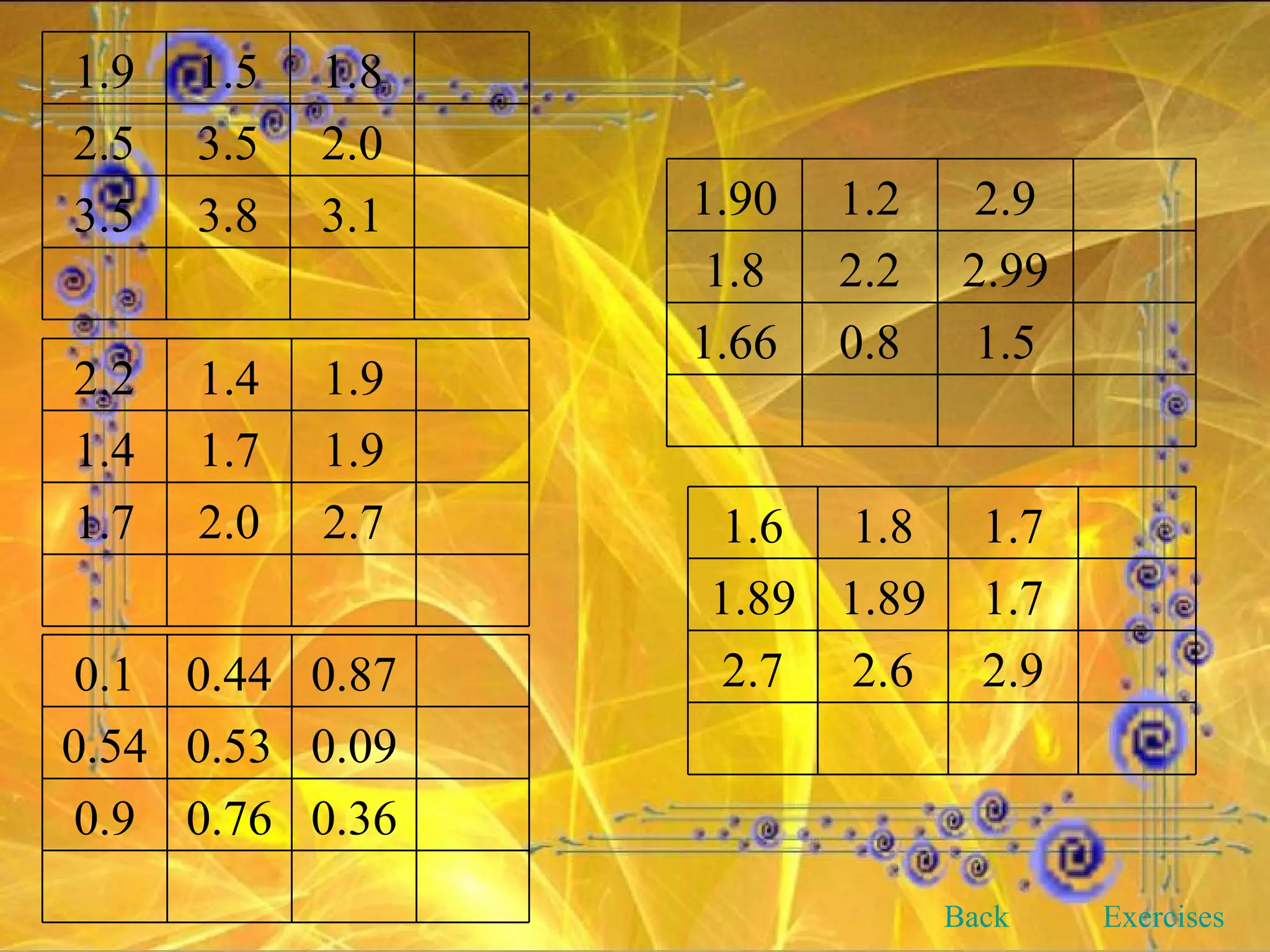
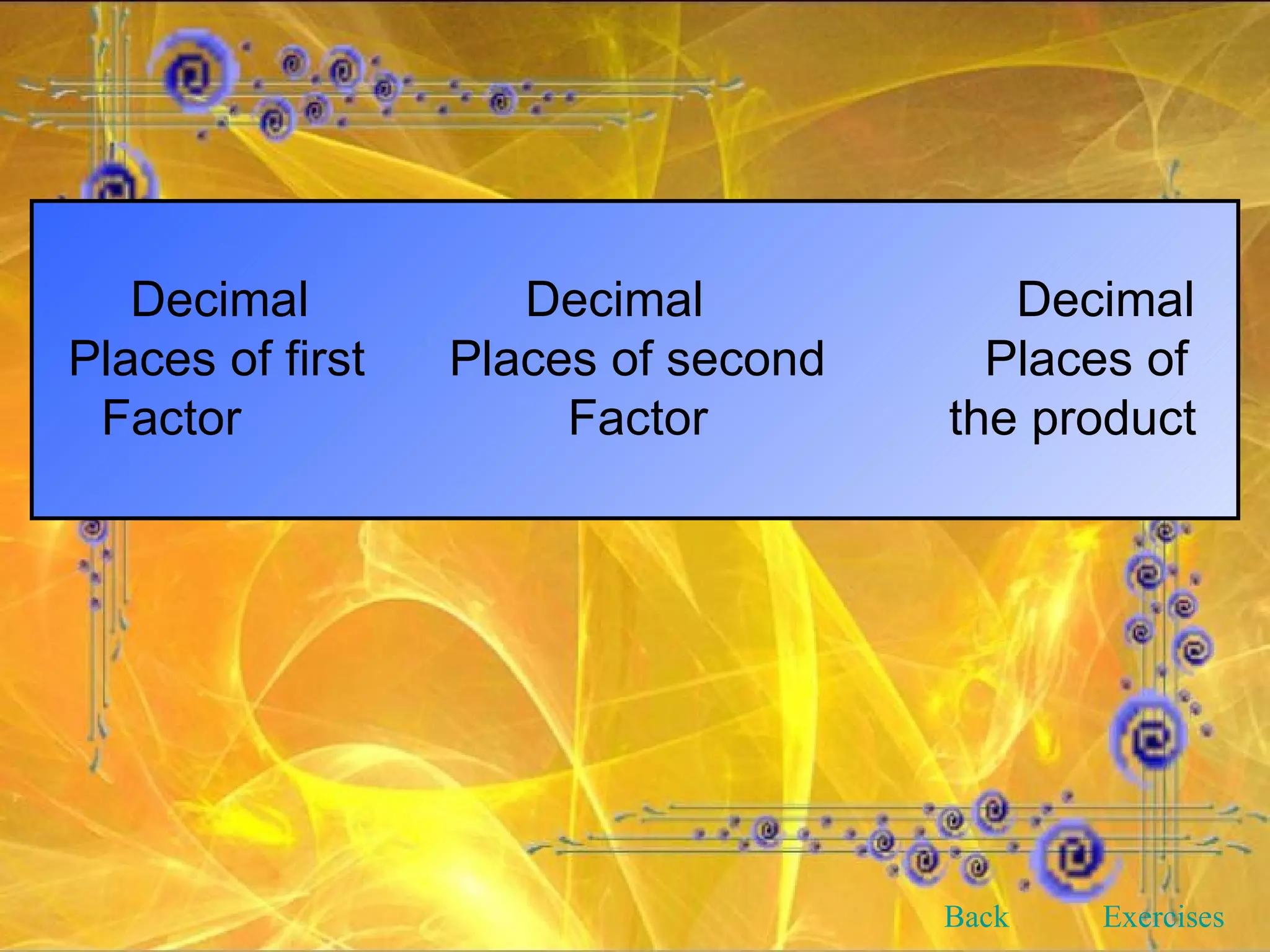
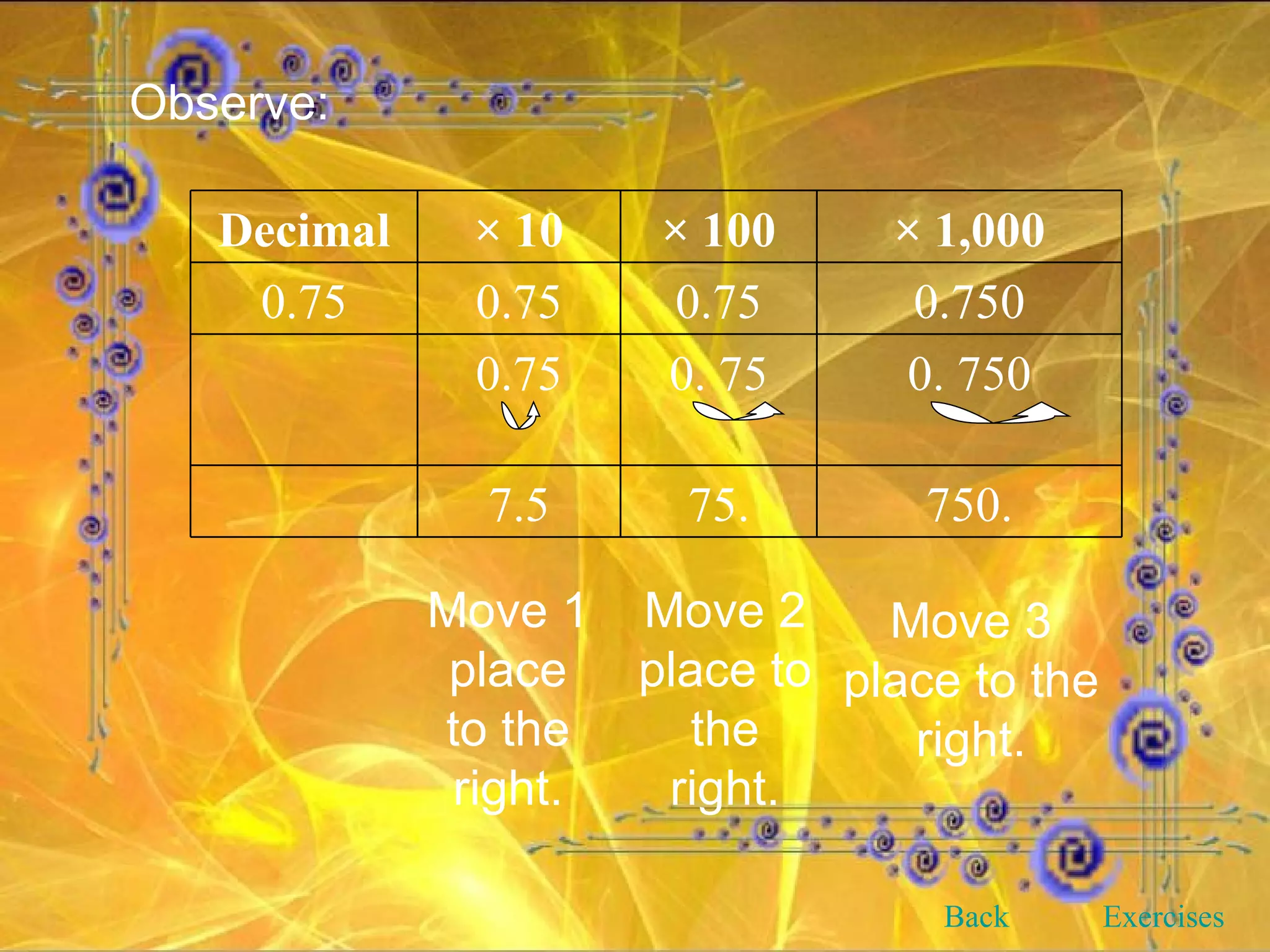
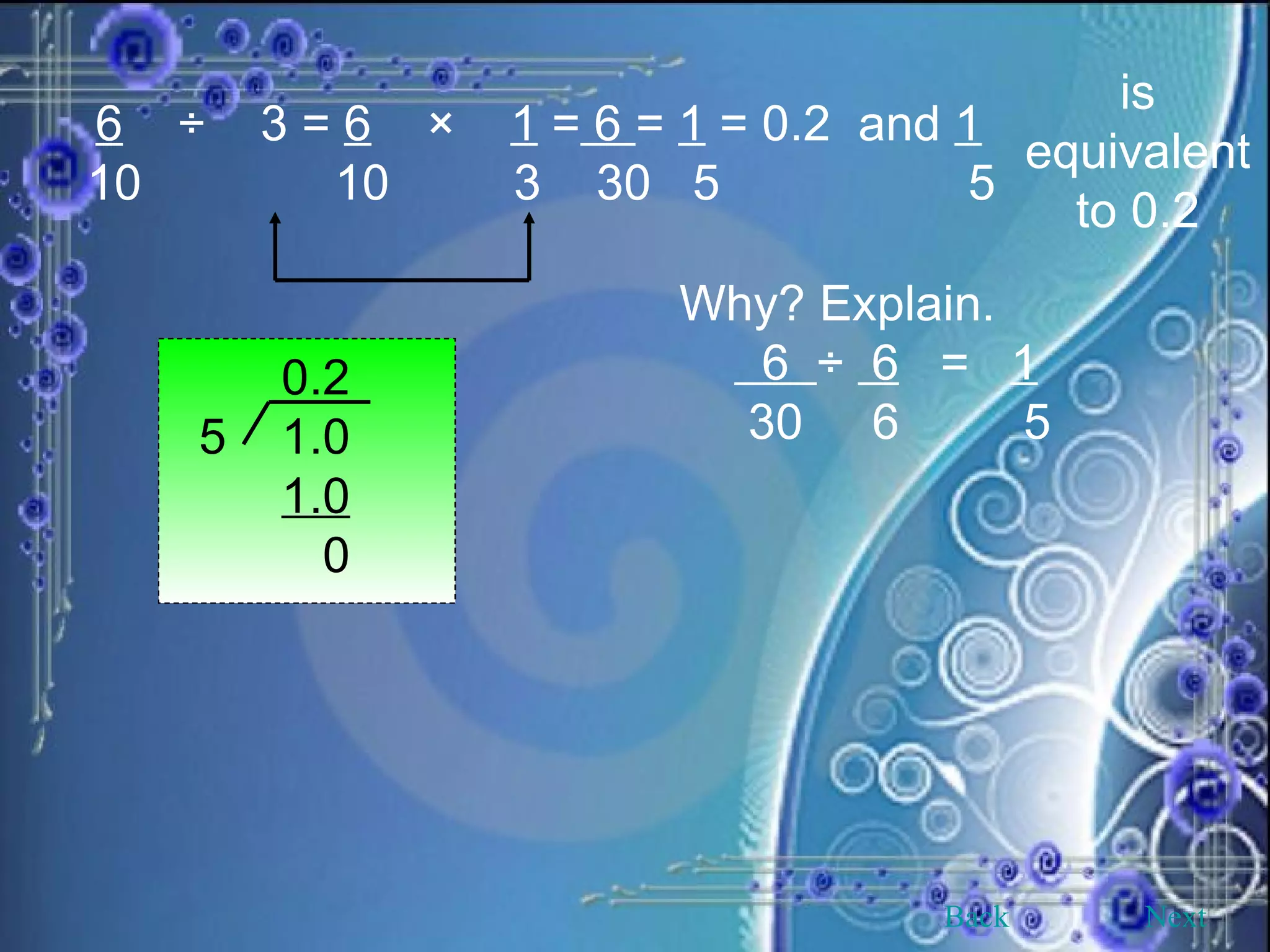
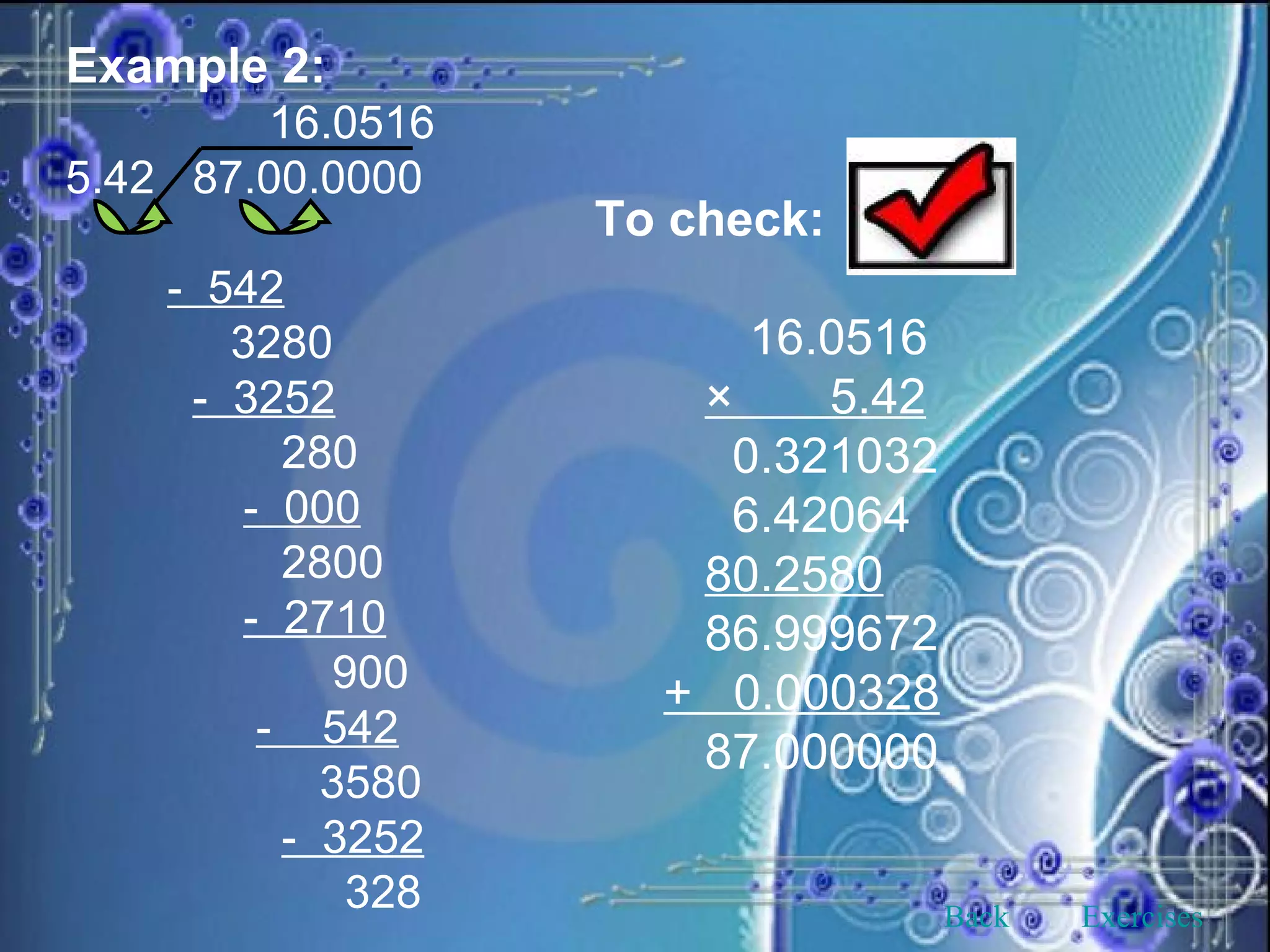
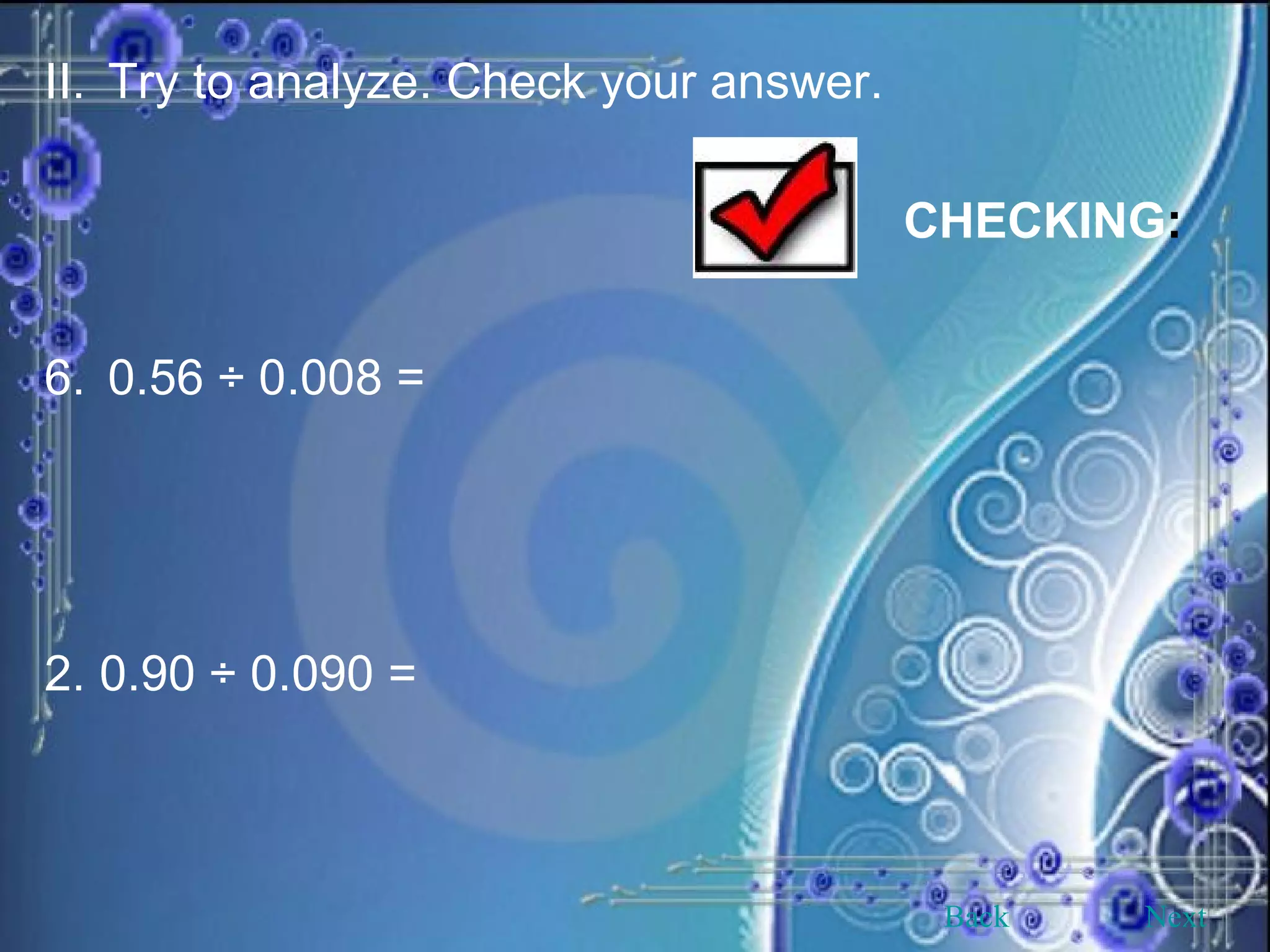
This document provides an overview and objectives of a modular workbook on learning decimal numbers for 6th grade students. It covers reading, writing, naming, comparing, ordering, and rounding decimal numbers. It also includes lessons on equivalent fractions and decimals, and the four arithmetic operations of addition, subtraction, multiplication and division of decimal numbers. The workbook aims to help students understand and work with decimal numbers in a fun and engaging way through various exercises and activities.












































































































































































































































































































































































![RON ANGELO A. DRONA Patricio Street, Brgy. San Jose Pangil, Laguna June 04, 1991 E-mail Address : [email_address] Back Next](https://image.slidesharecdn.com/decimalnumbers-090322034139-phpapp02/75/Decimal-Numbers-396-2048.jpg)

![BEATRIZ P. RAYMUNDO Brgy Bagong Pook Sta. Maria, Laguna April 21, 1951 E-mail Address : [email_address] Back Next](https://image.slidesharecdn.com/decimalnumbers-090322034139-phpapp02/75/Decimal-Numbers-398-2048.jpg)


![FOR-IAN V. SANDOVAL Siniloan, Laguna April 5, 1979 E-mail Address : [email_address] Back Next](https://image.slidesharecdn.com/decimalnumbers-090322034139-phpapp02/75/Decimal-Numbers-401-2048.jpg)






