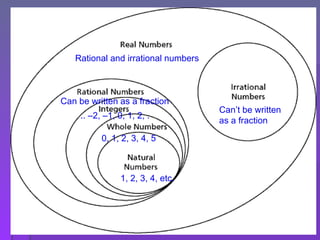
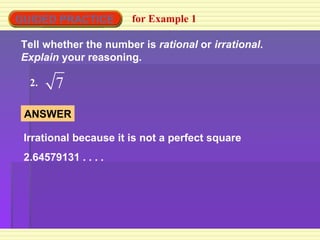
This document discusses rational and irrational numbers. It defines rational numbers as numbers that can be written as fractions or ratios, including integers, terminating decimals, and repeating decimals. Irrational numbers are defined as numbers that cannot be written as fractions or repeating/terminating decimals, such as the square root of a non-perfect square. Examples are provided to demonstrate how to determine if a number is rational or irrational based on its decimal representation.

1. Write the fraction as a decimal. Lesson 9.2 , For use with pages 475-480 1. 4 5 2. 5 9

2. Write the fraction as a decimal. Lesson 9.2 , For use with pages 475-480 ANSWER 0.8 1. 4 5 2. 5 9 ANSWER 0.5

3. RATIONAL and IRRATIONAL NUMBERS 9.2

4. Essential Questions What is the difference between an irrational number and a rational number? How are real numbers and the Pythagorean Theorem used in everyday life? What types of real-life situations could the Pythagorean Theorem or square roots apply to? Why?

5. Rational Numbers Rational numbers are simply numbers that can be written as fractions or ratios The hierarchy of real numbers looks something like this:

6. 1, 2, 3, 4, etc. 0, 1, 2, 3, 4, 5 .. –2, –1, 0, 1, 2, . Rational and irrational numbers Can be written as a fraction Can’t be written as a fraction

7. Rational Numbers : Any number that can be written in fraction form is a rational number . This includes integers, terminating decimals, and repeating decimals as well as fractions.

8. An integer can be written as a fraction simply by giving it a denominator of one, so any integer is a rational number .

9. A terminating decimal can be written as a fraction simply by writing it the way you say it: 3.75 = three and seventy-five hundredths = So, any terminating decimal is a rational number.

10. A repeating decimal can be written as a fraction using algebraic methods, so any repeating decimal is a rational number.

11. Irrational Numbers A number that cannot be expressed as a repeating or terminating decimal. An integer that is not a perfect square has an irrational root. REALS (the real numbers) The rational and irrational numbers.

12. Rational Number Fractions Ratios Whole numbers Integers Terminating decimals (stop) Repeating decimals Square root of a perfect square Irrational Numbers Non-terminating decimal Non-repeating decimal Square root of a number that is not a perfect square

13. GUIDED PRACTICE for Example 1 Tell whether the number is rational or irrational . Explain your reasoning. 5 8 1.

14. GUIDED PRACTICE for Example 1 Tell whether the number is rational or irrational . Explain your reasoning. 5 8 1. Rational because if we write it in its decimal form then it would be 0.625 which is terminating so it is a rational number ANSWER

15. GUIDED PRACTICE for Example 1 Tell whether the number is rational or irrational . Explain your reasoning. 2.

16. GUIDED PRACTICE for Example 1 Tell whether the number is rational or irrational . Explain your reasoning. 2. ANSWER Irrational because it is not a perfect square 2.64579131 . . . .

17. GUIDED PRACTICE for Example 1 Tell whether the number is rational or irrational . Explain your reasoning. 3.

18. GUIDED PRACTICE for Example 1 Tell whether the number is rational or irrational . Explain your reasoning. 3. ANSWER Rational because it is a perfect square

19. GUIDED PRACTICE for Example 1 Tell whether the number is rational or irrational . Explain your reasoning. 4. 2 9

20. GUIDED PRACTICE for Example 1 Tell whether the number is rational or irrational . Explain your reasoning. 4. 2 9 ANSWER Rational because if we write it in its decimal from then it would be 0.2 where 2 repeating so it is a rational number

21. EXAMPLE 1 Number Rational Rational Irrational Terminating Repeating Non terminating and non repeating Classifying Real Numbers Type Decimal Form Type of Decimal a. 3 4 b. 1 11 c. 3 11 1 = 0.0909… = 0.09 3 = 1.7320508 . . . 3 4 = 0.75 3

22. Examples Which of the following are irrational numbers? 1. Irrational 2. Rational -30 3. Rational 74 4. Irrational

23. Homework Page 477 #1-15 Problems 3-14 will be two points each One point for rational or irrational One point for the reason