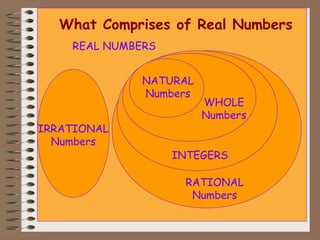
This document defines and provides examples of different types of real numbers: - Real numbers include all natural numbers, whole numbers, integers, rational numbers, and irrational numbers. They comprise every number that can be found on the number line. - Natural numbers are counting numbers starting from 1. Whole numbers are natural numbers with 0 added. Integers include natural numbers and their negatives. Rational numbers are numbers that can be written as fractions. Irrational numbers are numbers that cannot be written as fractions. 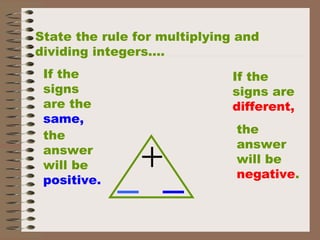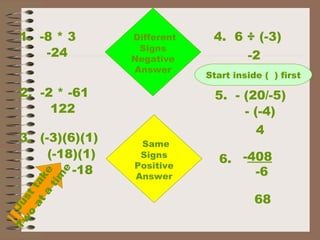- Examples demonstrate addition and subtraction of integers using rules such as keeping the sign the same for addition/subtraction of like signs, and changing the sign for addition/subtraction of opposite signs. Multiplication and division

1. REAL NUMBERS
Made By-: Jai Hans
Class -: IX
Section-: B
Roll No-:4
Admission No-: 3077

2. Real Numbers
• Real Numbers are every number.
• Therefore, any number that you can
find on the number line.
• Real Numbers are the compilation of
all types of numbers.

3. WHOLE
Numbers
REAL NUMBERS
IRRATIONAL
Numbers
NATURAL
Numbers
RATIONAL
Numbers
INTEGERS
What Comprises of Real Numbers

4. Natural Numbers
•All counting numbers
which start from 1
are natural numbers.
•They have only
positive value
numbers.

5. Whole Numbers
Whole Numbers are
natural numbers with
the number 0 added
to them.
They have one
number zero as
neither positive nor
negative but all other
numbers are positive.

6. Integers
•Integers are natural
numbers with zero
and their negative
values.
•They have a neutral
number zero, the positive numbers
with their negative
counterparts.

7. Rational Numbers
Rational numbers are those numbers
which cannot be written as integers.
They are written as integer divided
by another integer and the denominator
is not zero and both numbers do not
have common factors.
Rational numbers have either ending or
non-terminating repeating decimal
expansions
Between every 2 rational numbers, we
will find 2more
rational numbers.
Rational numbers can be called fractions.

8. Irrational Numbers
• A number which cannot be
written as an integer upon integer
where the denominator is zero
and both integers are co-primes
are irrational numbers.
• They are non –terminating non-
repeating decimal expansions.
• The roots of prime number are
irrational.

9. Real Numbers
REAL NUMBERS
-8
-5,632.1010101256849765…
61
49%
π
549.23789
154,769,852,354
1.333

10. Examples: Use the number line
if necessary.
4
2) (-1) + (-3) =
-4
3) 5 + (-7) =
-2
0 5-5
1) (-4) + 8 =

11. Addition Rule
1) When the signs are the same,
ADD and keep the sign.
(-2) + (-4) = -6
2) When the signs are different,
SUBTRACT and use the sign of the
larger number.
(-2) + 4 = 2
2 + (-4) = -2

12. -1 + 3 = ?
1. -4
2. -2
3. 2
4. 4
Answer Now

13. -6 + (-3) = ?
1. -9
2. -3
3. 3
4. 9
Answer Now

14. The additive inverses (or
opposites) of two numbers add
to equal zero.
-3
Proof: 3 + (-3) = 0
We will use the additive
inverses for subtraction
problems.
Example: The additive inverse of 3 is

15. What’s the difference
between
7 - 3 and 7 + (-3) ?
7 - 3 = 4 and 7 + (-3) = 4
The only difference is that 7 - 3 is a
subtraction problem and 7 + (-3) is an
addition problem.
“SUBTRACTING IS THE SAME AS
ADDING THE OPPOSITE.”
(Keep-change-change)

16. When subtracting, change the
subtraction to adding the opposite
(keep-change-change) and then follow
your addition rule.
Example #1: - 4 - (-7)
- 4 + (+7)
Diff. Signs --> Subtract and use larger sign.
3
Example #2: - 3 - 7
- 3 + (-7)
Same Signs --> Add and keep the sign.
-10

17. Which is equivalent to
-12 – (-3)?
Answer Now
1. 12 + 3
2. -12 + 3
3. -12 - 3
4. 12 - 3

18. 7 – (-2) = ?
Answer Now
1. -9
2. -5
3. 5
4. 9

19. State the rule for multiplying and
dividing integers….
If the
signs
are the
same,
If the
signs are
different,
+
the
answer
will be
positive.
the
answer
will be
negative.

20. 1. -8 * 3 What’s
The
Rule?
Different
Signs
Negative
Answer
-24
2. -2 * -61
Same
Signs
Positive
Answer
122
3. (-3)(6)(1)
Justtake
Tw
o
ata
tim
e
(-18)(1)
-18
4. 6 ÷ (-3)
-2
5. - (20/-5)
- (-4)
4
6.
68
Start inside ( ) first
-408
-6