number system

NUMBER SYSTEM
BY :
IKA KOMALA SARI
NILA PATMALA
R. ULFAHTUL HASANAH
VIERA VIRLIANI
B.INGGRIS MATEMATIKA

Number
System
1.1
1.2
1.5
1.6
1.3 1.7
1.8
1.9
Exit
1.4
NUMBER SYSTEM
Human beings have trying to have a count
of their belonging, goods, ornaments,
jewels, animals, trees, goats, etc. by using
techniques.
1. putting scratches on the ground
2. by storing stones-one for each
commodity kept taken out
This was the way of having a count of their
belongings without knowledge of counting

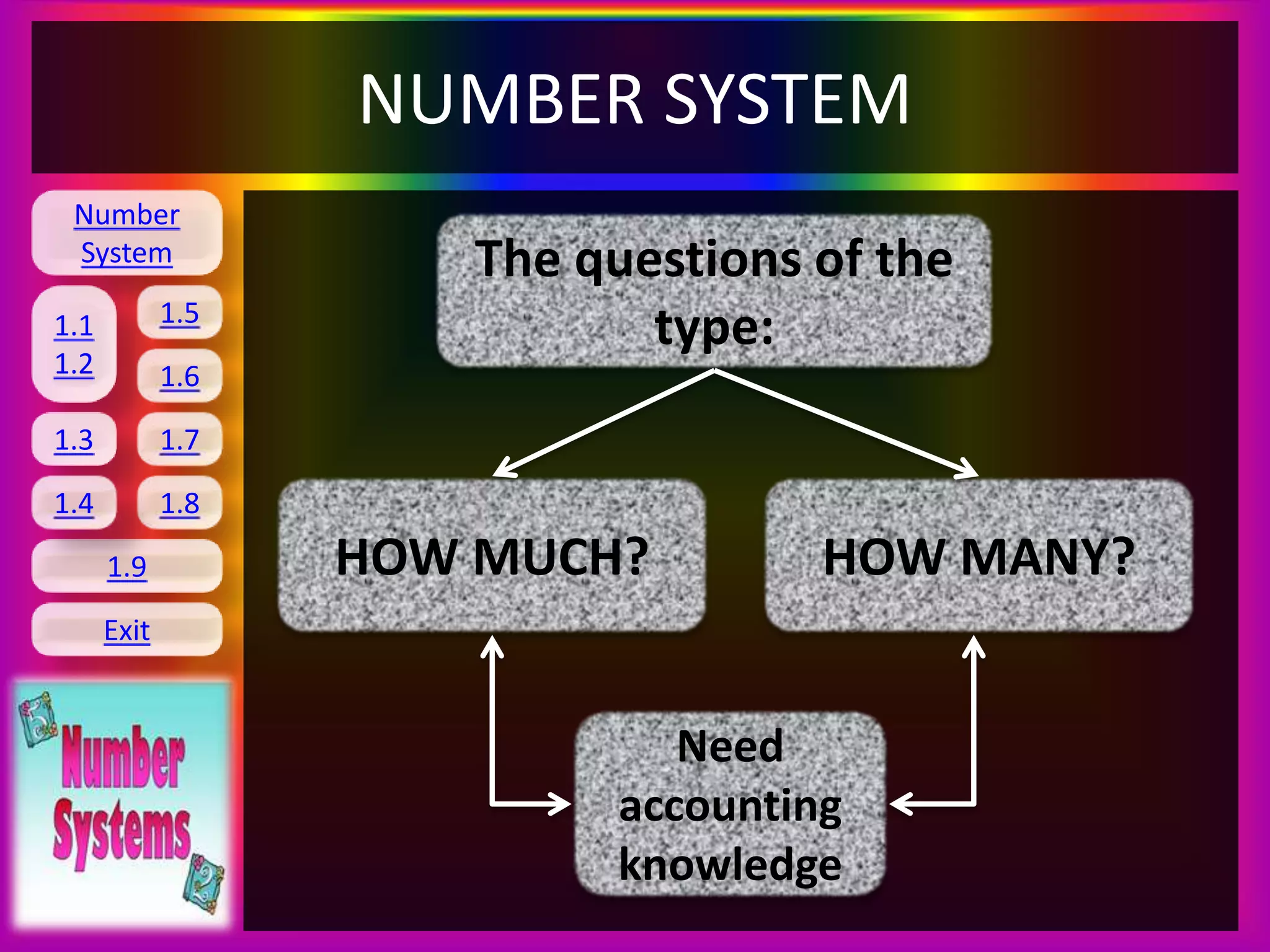
Number
System
1.1
1.2
1.5
1.6
1.3 1.7
1.8
1.9
Exit
1.4
NUMBER SYSTEM
The questions of the
type:
HOW MUCH? HOW MANY?
Need
accounting
knowledge

Number
System
1.1
1.2
1.5
1.6
1.3 1.7
1.8
1.9
Exit
1.4
The functions of learning number
system
Are 11 functions, that to:
Illustrate the extension of system of
number from natural number to real
(rational and irrational) numbers
Identify different types of numbers
Express an integers as a rational number
Express a rational number as a terminating
or non-terminating repeating decimal and
vice-versa

Number
System
1.1
1.2
1.5
1.6
1.3 1.7
1.8
1.9
Exit
1.4
system
Find rational numbers between any two
rationals
Represent a rational number on the
number line
Cites example of irrational numbers
Represent 2, 3, 4 on the number line
Find irrational numbers between any
two given numbers
2 3 4

Number
System
1.1
1.2
1.5
1.6
1.3 1.7
1.8
1.9
Exit
1.4
system
Round off rational and irrational
numbers to given number of decimal
places
Perform the four fundamental
operation of addition, subtraction,
multiplication, and division on real
numbers

Number
System
1.1
1.2
1.5
1.6
1.3 1.7
1.8
1.9
Exit
1.4
1.1 EXPECTED BACKGROUND
KNOWLEDGE
It is about the accounting numbers in
use on the day to day life
Accounting
numbers
Day life

Number
System
1.1
1.2
1.5
1.6
1.3 1.7
1.8
1.9
Exit
1.4
1.2 Recall of Natural Numbers, Whole
Numbers, and Integers
Natural Numbers
1, 2, 3, …
There is no greatest natural number,
for if 1 added to any natural numbers. we
get the next higher natural number, call
its successor.
Example :
4+2=6
12:2=6
22-6=16
12×3=36

Number
System
1.1
1.2
1.5
1.6
1.3 1.7
1.8
1.9
Exit
1.4
Addition and multiplication of natural
numbers again yield a natural numbers
But the subtraction and division of
two natural number may or may not yield
a natural numbers
Example:
Number line of natural numbers
1 2 3 4 5 6 7 8 9 …
2-6 = -4 6 : 4 = 3/2

Number
System
1.1
1.2
1.5
1.6
1.3 1.7
1.8
1.9
Exit
1.4
Whole Numbers
The natural number were extended by
zero (0)
0, 1, 2, 3, …
There is no greatest whole numbers
The number 0 has the following
properties:
a+0 = a = 0+a
a-0 = a but 0-a is not defined in whole
numbers
a×0 = 0 = 0×a
Division by 0 is not defined

Number
System
1.1
1.2
1.5
1.6
1.3 1.7
1.8
1.9
Exit
1.4
The whole number in four
fundamental operation is same
The line number of whole number
0 1 2 3 4 5 6 7 …

Number
System
1.1
1.2
1.5
1.6
1.3 1.7
1.8
1.9
Exit
1.4
Integers
Another extension of numbers
which allow such subtractions. It is
begin from negative numbers until the
whole number.
The number line of integers
… -3 -2 -1 0 1 2 3 4 …

Number
System
1.1
1.2
1.5
1.6
1.3 1.7
1.8
1.9
Exit
1.4
Representing Integers on number line
A B C D
… -4 -3 -2 -1 0 1 2 3 4 5 …
Then A = -3 C = 2
B = -1 D = 3
A < B, D > C, B < C, C > A
The rule:
1. A > B, if A is to the right of B
2. A < B, if A is to the left of B

Number
System
1.1
1.2
1.5
1.6
1.3 1.7
1.8
1.9
Exit
1.4
1.3 Rational Number
Rational Numbers
Consider the situation, when an
integer a is divided by another non-zero
integer b. The following case arise:
1. When A multiple of B
A = MB, where M is natural number or
integer. Then, A/B =M

Number
System
1.1
1.2
1.5
1.6
1.3 1.7
1.8
1.9
Exit
1.4
1.3 Rational Number
2. Rational number is when A is not A
multiple B. A/B is not an integer. Thus,
a number which can be put in the form
p/q, where p and q are integers and q
≠ 0.
Example:
All Rational
Numbers
-2 5 6 11
3 -8 2 7

Number
System
1.1
1.2
1.5
1.6
1.3 1.7
1.8
1.9
Exit
1.4
1.3 Rational Number
Positive and Negative Rational Number
1. p/q is said positive numbers if p and
q are both positive or both negative
integers
2. p/q is said negative if p and q are of
different sign. Example:
+ -
3
4
-1
-5
-7
4
6
-5

Number
System
1.1
1.2
1.5
1.6
1.3 1.7
1.8
1.9
Exit
1.4
1.3 Rational Number
Standard Form of a Rational Number
We can see that
-p/q = -(p/q)
-p/-q = -(-p)/-(-q)= p/q
p/-q= (-p)/q
-p p -p p
q -q -q q

Number
System
1.1
1.2
1.5
1.6
1.3 1.7
1.8
1.9
Exit
1.4
1.3 Rational Number
Notes:
A rational number is standard form
is also referred to as “a rational lowest
form” . There are two terms
interchangeably
Example:
18/27 can be written 2/3 in
standard form (lowest form)

Number
System
1.1
1.2
1.5
1.6
1.3 1.7
1.8
1.9
Exit
1.4
1.3 Rational Number
Some important
result:
1. Every natural number is a rational
number but vice-versa is not always
true
2. Every whole number and integer is a
rational number but vice-versa is not
always true

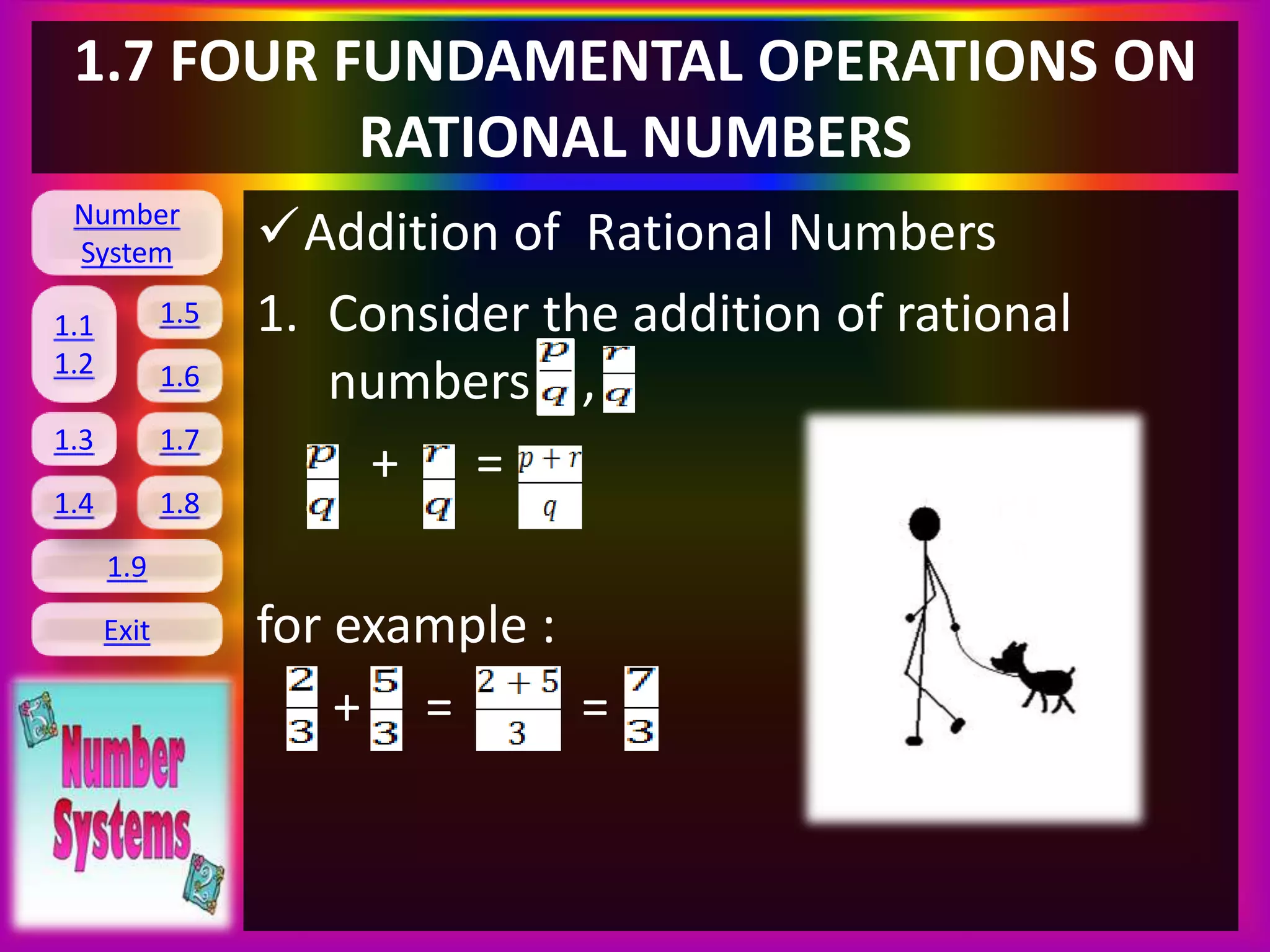
Number
System
1.1
1.2
1.5
1.6
1.3 1.7
1.8
1.9
Exit
1.4
1.7 FOUR FUNDAMENTAL OPERATIONS ON
RATIONAL NUMBERS
Addition of Rational Numbers
1. Consider the addition of rational
numbers ,
+ =
for example :
+ = =

Number
System
1.1
1.2
1.5
1.6
1.3 1.7
1.8
1.9
Exit
1.4
1.7 FOUR FUNDAMENTAL OPERATIONS
ON RATIONAL NUMBERS
2. Consider the two rational numbers p/q
and r/s
p/q + r/s = ps/qs + rq/sq =
for example :
¾ + 2/3 = = =

Number
System
1.1
1.2
1.5
1.6
1.3 1.7
1.8
1.9
Exit
1.4
ON RATIONAL NUMBERS
from the above two cases, we
generalise the following rule:
(a)The addition of two rational numbers
with common denominator is the
rational number with common
denominator and numerator as the
sum of the numerators of the two
rational numbers.

Number
System
1.1
1.2
1.5
1.6
1.3 1.7
1.8
1.9
Exit
1.4
ON RATIONAL NUMBERS
b)The sum of two rational numbers with
different denominator is a rational
number with the denominator equal to
the product of the denominators of
two rational numbers and the
numerator equal to sum of product of
the numerator of first rational with the
denominator of second and the product
of numerator of second rational
number and the denominator of the
first rational number.

Number
System
1.1
1.2
1.5
1.6
1.3 1.7
1.8
1.9
Exit
1.4
ON RATIONAL NUMBERS
Examples:
Add the following rational numbers :
(i) 2/7 and 6/7
(ii) 4/17 and -3/17
Solution:
(i) 2/7 + 6/7 = 8/7
(ii) 4/17 + (-3)/17 = 1/17

Number
System
1.1
1.2
1.5
1.6
1.3 1.7
1.8
1.9
Exit
1.4
ON RATIONAL NUMBERS
Add each of the following rational
numbers, examples:
(i) 3/4 and 1/7
Solution :
(i) we have 3/4 + 1/7
= 3x7/4x7 + 1x4/7x4
= 21/28 + 4/28 = 25/28
3/4 + 1/7 = 25/28 or 3x7+4x1 / 4x7
= 21+4/728 = 25/28

Number
System
1.1
1.2
1.5
1.6
1.3 1.7
1.8
1.9
Exit
1.4
ON RATIONAL NUMBERS
Subtraction of Rational Numbers
(a) p/q – r/q = p-r/q
Example :
7/4 – ¼ = …
7/4 –1/4 = 7 – 1
4
= 6/4 = 2x3 = 3/2
2x2
3/5 – 2/15 = …
3x12/5x12 – 2x5/12x5
= 36/60 – 10/60
= 26/60
= 13x2/30x2
= 13/30

Number
System
1.1
1.2
1.5
1.6
1.3 1.7
1.8
1.9
Exit
1.4
ON RATIONAL NUMBERS
 Multiplication and Division of Rational
Numbers
(i) Multiplication of two rational number (p/q) and (r/s) ,
q 0, s 0 is the
rational number pr/ps where qs 0
= product of numerators/product of
denominators
(ii) Division of two rational numbers p/q and r/s , such that
q 0, s 0, is the
rational number ps/qr, where qr 0
In the other words (p/q) (r/s) = p/r x (s/r)
Or (First rational number) x (Reciprocal of the second rational
number)
Let us consider some examples

Number
System
1.1
1.2
1.5
1.6
1.3 1.7
1.8
1.9
Exit
1.4
ON RATIONAL NUMBERS
Examples :
(i) 3/7 and 2/9 (ii) 5/6 and (-2/19)
Solution :
(i) 3/7 x 2/9 = 3x2/7x9 = 3x2/7x3x3 = 2/21
(3/7))x(2/9) = 2/21
(ii) 5/6 x (-2/19) = 5x(-2)/6x19 = - 2x5/2x3x19
= -5/57
5/6 x (-2/19) = -5/57

Number
System
1.1
1.2
1.5
1.6
1.3 1.7
1.8
1.9
Exit
1.4
ON RATIONAL NUMBERS
(i) (3/4) (7/12)
Solution:
(i) (3/4) (7/12)
= (3/4) x (12/7) [Reciplocal of 7/12 is 12/7]
= 3x12/4x7 = 3x3x4/7x4 = 9/7
(3/4) (7/12) = 9/7

Number
System
1.1
1.2
1.5
1.6
1.3 1.7
1.8
1.9
Exit
1.4
1.8 DECIMAL REPRESENTATION OF A
RATIONAL NUMBER
You are familiar with the division of an
integer by another integer and
expressing the result as a decimal
number. The process of expressing
rational number into decimal from is to
carryout the process of long division
using decimal notation. Example:
Represent each one the following into a
decimal number (i) (ii) :
5
12
25
27

Number
System
1.1
1.2
1.5
1.6
1.3 1.7
1.8
1.9
Exit
1.4
RATIONAL NUMBER
Solution: Using long division, we get
(i)
Hence , = 2,4
(ii) (-1, 08)
hence, = -1, 08
4,2
0,2
0,2
10
,12
5
x
5
12
x
200
200
25
27
25

25
27

Number
System
1.1
1.2
1.5
1.6
1.3 1.7
1.8
1.9
Exit
1.4
RATIONAL NUMBER
From the above example, it can be
seen that the division process stops after a
finite number of steps, when the
remainder becomes zero and the resulting
decimal number has a finite number of
decimal places. Such decimals are known
as terminating decimals.
Note that in the above division, the
denominators of the rational numbers had
only 2 or 5 or both as the only prime
factor

Number
System
1.1
1.2
1.5
1.6
1.3 1.7
1.8
1.9
Exit
1.4
RATIONAL NUMBER
Alternatively, we could have written as
= = 2,4
Other examples:
Here the remainder 1 repeats.
The decimal is not a terminating
decimal
= 2,333… or 2,3
5
12
25
212
x
x
10
24
33,2
00,1
9
0,1
6
00,7
3
3
7

Number
System
1.1
1.2
1.5
1.6
1.3 1.7
1.8
1.9
Exit
1.4
RATIONAL NUMBER
` = 0,2
85714 Note: A bar over a digit or a
group of digits implies that
digit or group of digits starts
repeating itself
indefinitely.
28571428,0
4
56
60
14
20
28
30
7
10
49
50
35
40
56
60
14
000.2
7
7
2

Number
System
1.1
1.2
1.5
1.6
1.3 1.7
1.8
1.9
Exit
1.4
RATIONAL NUMBER
Expressing decimal expansion of
rational number in p/q form
Examples:
Express in form p/q !
Express in in form p/q !
0,48
=100
48
25
12
Let x = 0,666 (A)
10 x = 6,666 (B)
(B)-(A) gives 9x = 6 or
x = 2/3
0,666
The example
above
illustrates that:
A terminating
decimal or a
non-
terminating
recurring
decimal
represents a
rational number

Number
System
1.1
1.2
1.5
1.6
1.3 1.7
1.8
1.9
Exit
1.4
RATIONAL NUMBER
Note :
The non-terminating recurring
decimals like 0,374374374… are
written as 0,374.
The bar on the group of digits 374
indicate that group of digits repeats
again and again.

Number
System
1.1
1.2
1.5
1.6
1.3 1.7
1.8
1.9
Exit
1.4
1.9 RATIONAL NUMBERS BETWEEN
TWO RATIONAL NUMBERS
Is it possible to find a rational
number between two given rational
numbers. To explore this, consider the
following example.
Example : Find rational number
between and
Let us try to find the number ( + )
( ) = now, = =
And = =
4
3
5
6
2
1
4
3
5
6
2
1
20
2415
40
39
4
3
104
103
x
x
40
30
5
6
85
86
x
x
40
48
abviously, < <40
30
40
39
40
48

Number
System
1.1
1.2
1.5
1.6
1.3 1.7
1.8
1.9
Exit
1.4
1.9 RATIONAL NUMBERS BETWEEN
TWO RATIONAL NUMBERS
is a rational number between the
rational numbers and
Note : = 0,75. = 0, 975 and = 1,2
Than: 0,75 < 0, 975 < 1,2
This can be done by either way :
(i) reducing each of the given rational
number with a common base and then
taking their average
(ii) by finding the decimal expansions of
the two given rational numbers and
then taking their average
4
340
39
5
6
4
3
40
39
5
6

Number
System
1.1
1.2
1.5
1.6
1.3 1.7
1.8
1.9
Exit
1.4
1.4 Equivalent Forms of a Rational
Number
A rational number can be written in
an equivalent form by multiplying or
dividing the numerator and denominator
of the given rational number by the same
number
Example :
2/3 = 2x2 = 4/6 and 2/3 = 2x4 = 8/12
3x2 3x8
It’s mean 4/6 and 8/12 are
equivalent form of the rational number
2/3

Number
System
1.1
1.2
1.5
1.6
1.3 1.7
1.8
1.9
Exit
1.4
1.5 Rational Numbers on the Number
Line
We know how to represent intergers on
the number line. Let us try to represent
½ on the number line. The rational
number ½ is positive and will be
represented to the right of zero. As
0<½<1, ½ lies between 0 and 1. divide
the distance OA in two equal parts. This
can be done by bisecting OA at P

Number
System
1.1
1.2
1.5
1.6
1.3 1.7
1.8
1.9
Exit
1.4
1.5 Rational Numbers on the Number
Line
Let P represet ½. Similarly R, the mid-
point of OA’, represents the rational
number -½.
A R 0 P A
… -2 -1 0 1 2 3 …
Similarly , can be represented on the
number line as below:
B’ A’ O A P B C
… -2 -1 0 1 2 3 …
As 1 < 4/3 < 2 therefore, 4/3 between 1 and 2
3
4
-1/2 1/2
4/3

Number
System
1.1
1.2
1.5
1.6
1.3 1.7
1.8
1.9
Exit
1.4
1.6 COMPARISON OF RATION NUMBER
In order to compare to rational
number, we follow any of the following
methods:
(i)If two rational numbers, to be compare
have the same denominator compare
their numerators. The number having
the greater numerator is the greater
rational number. Thus for the two
rational numbers and , with the
same positive denominator.
as 9>5. so,
17
5
17
9
17
5
17
9
,17 
17
5
17
9


Number
System
1.1
1.2
1.5
1.6
1.3 1.7
1.8
1.9
Exit
1.4
(ii) If two rational number are having
different denominator, make ther
denominator equal by taking their
equivalent form and then compare the
numerator of the resulting rational
numbers. The number having a greater
numerator is greater rational number.
For example, to compare two rational
numbers and , we first make their
denominator same in the following manner:
7
3
11
6

Number
System
1.1
1.2
1.5
1.6
1.3 1.7
1.8
1.9
Exit
1.4
(iii) By plotting two given rational
numbers on the number line we see
that rational number to the righ of the
other rational number is greater.
77
33
117
113

x
x
77
42
711
79

x
x
As 42>33, or
77
33
77
42

7
3
11
6


Number
System
1.1
1.2
1.5
1.6
1.3 1.7
1.8
1.9
Exit
1.4
For example, take and , we plot
these number on the number line as
below:
-2 -1 0 1 2 3
3
2
4
3

Number
System
1.1
1.2
1.5
1.6
1.3 1.7
1.8
1.9
Exit
1.4
0<⅔<1 and 0< ¾<1. it means ⅔ and ¾
both lie between 0 and 1. by the
method of diving a line Into equal
number of parts, A represent ⅔ and B
represent ¾
As B is to the right of A, ¾>⅔ or ⅔<¾
So, out of ⅔ and ¾, ¾ is greter number.

Number
System
1.1
1.2
1.5
1.6
1.3 1.7
1.8
1.9
Exit
1.4
Thank’s for your attention

number system

More Related Content

What's hot

Viewers also liked

Similar to number system

Recently uploaded

number system