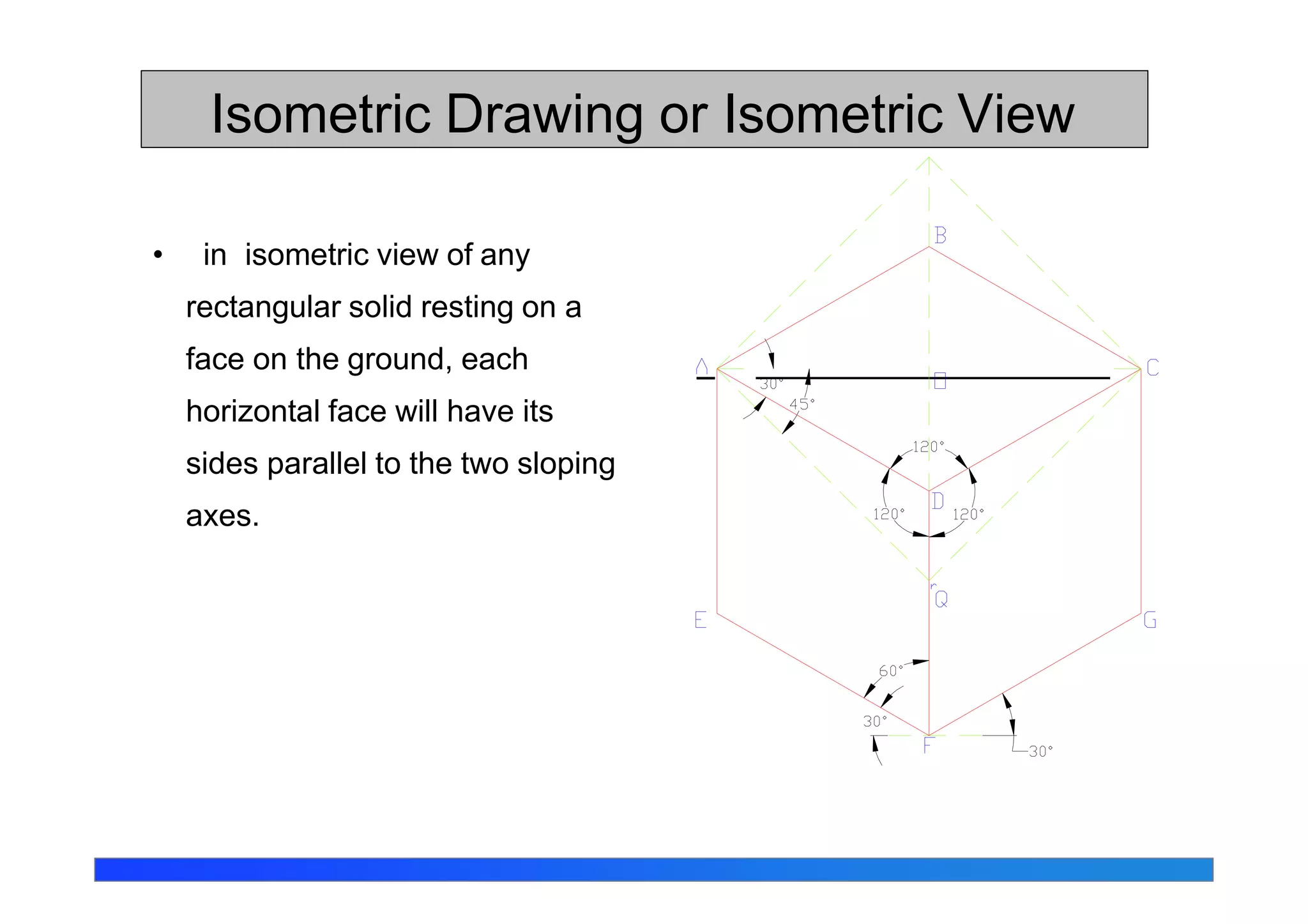
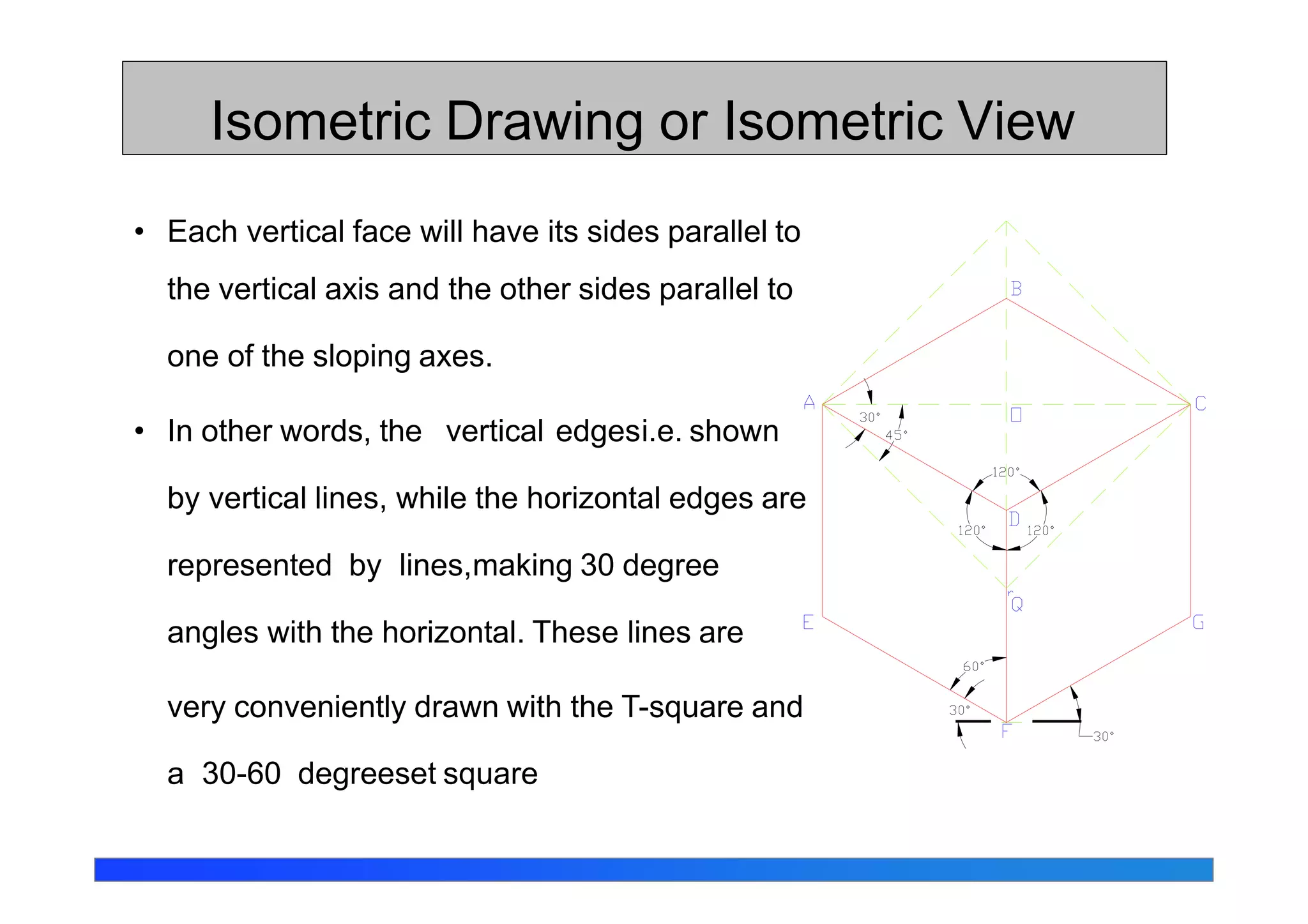
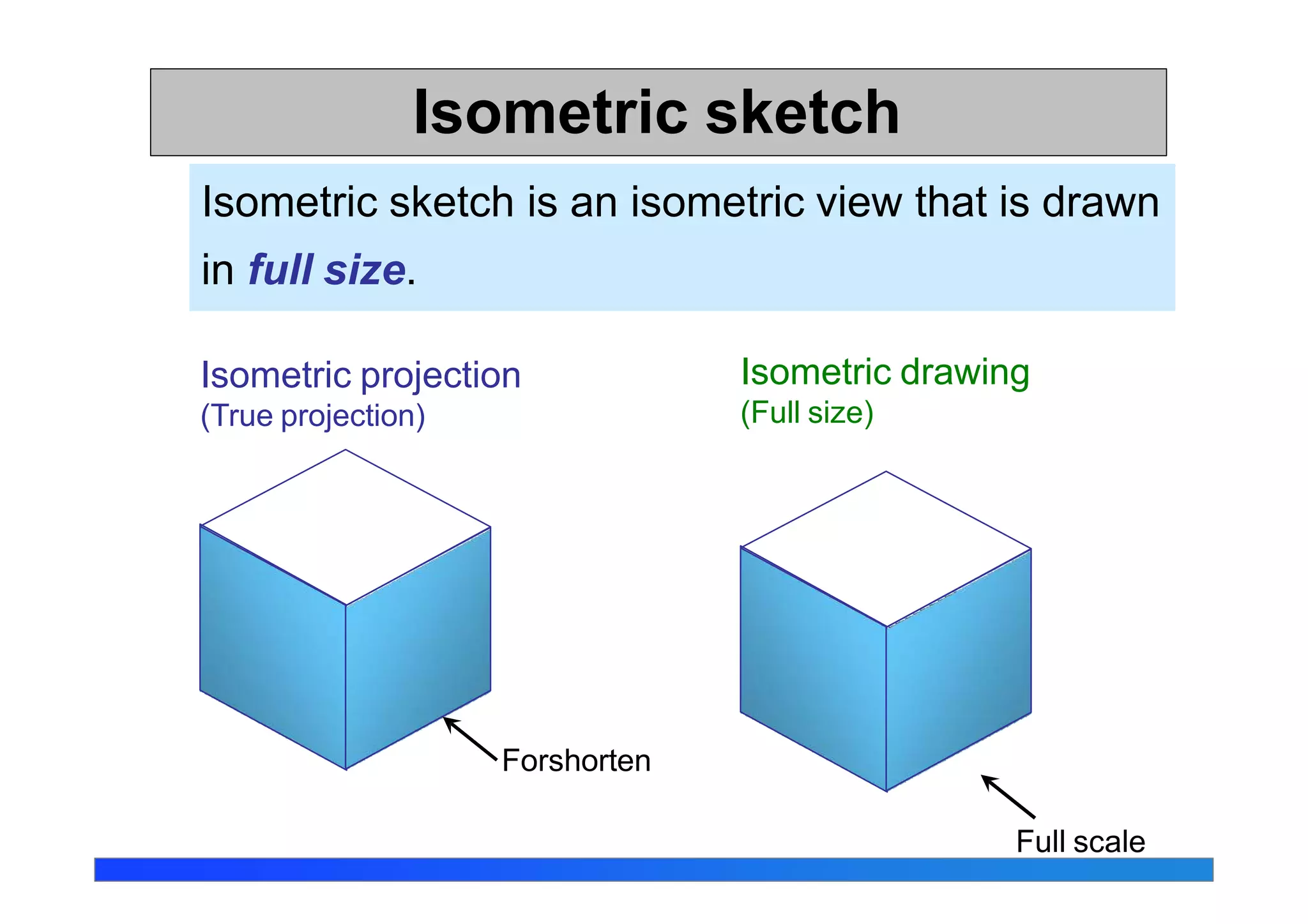
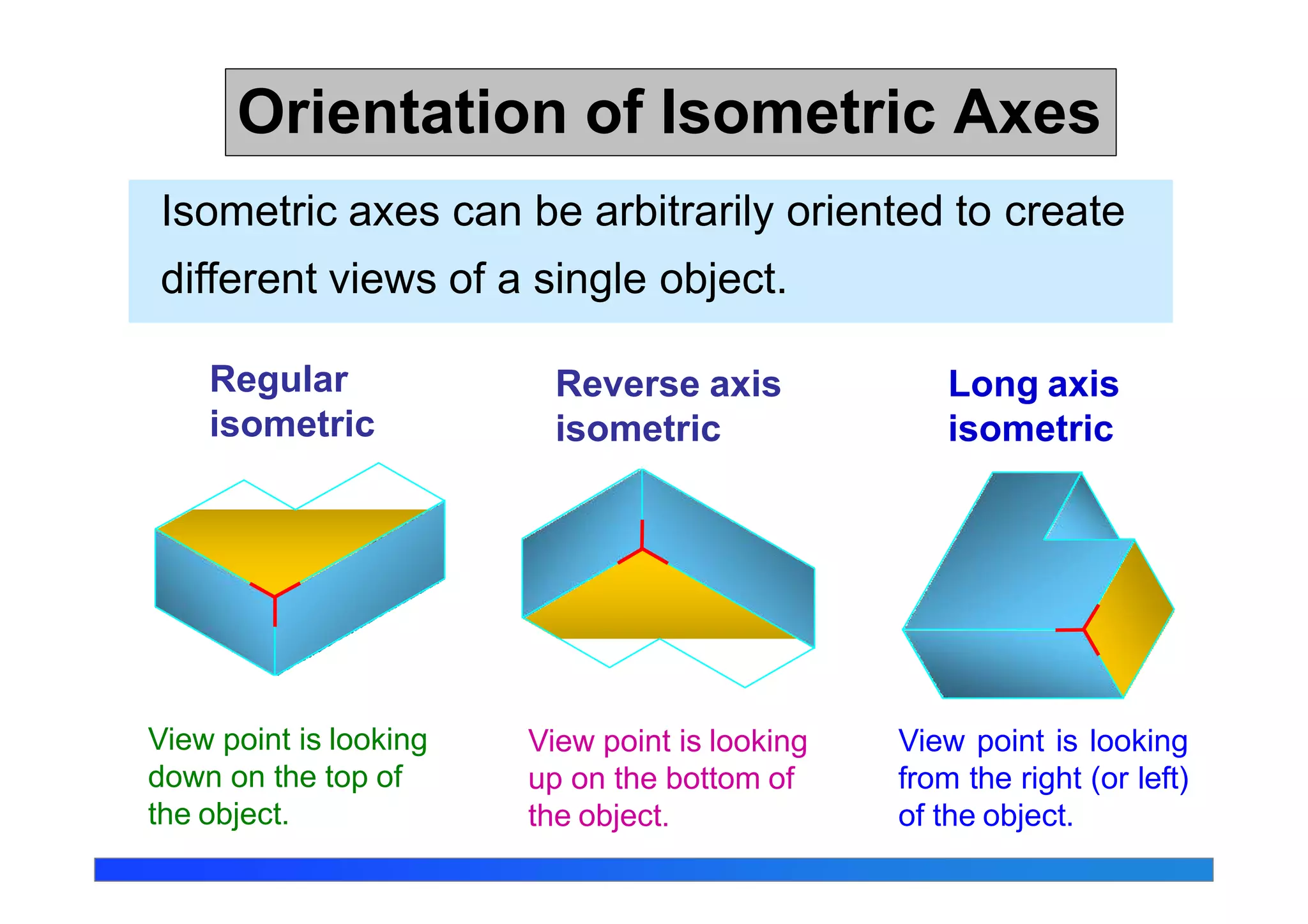
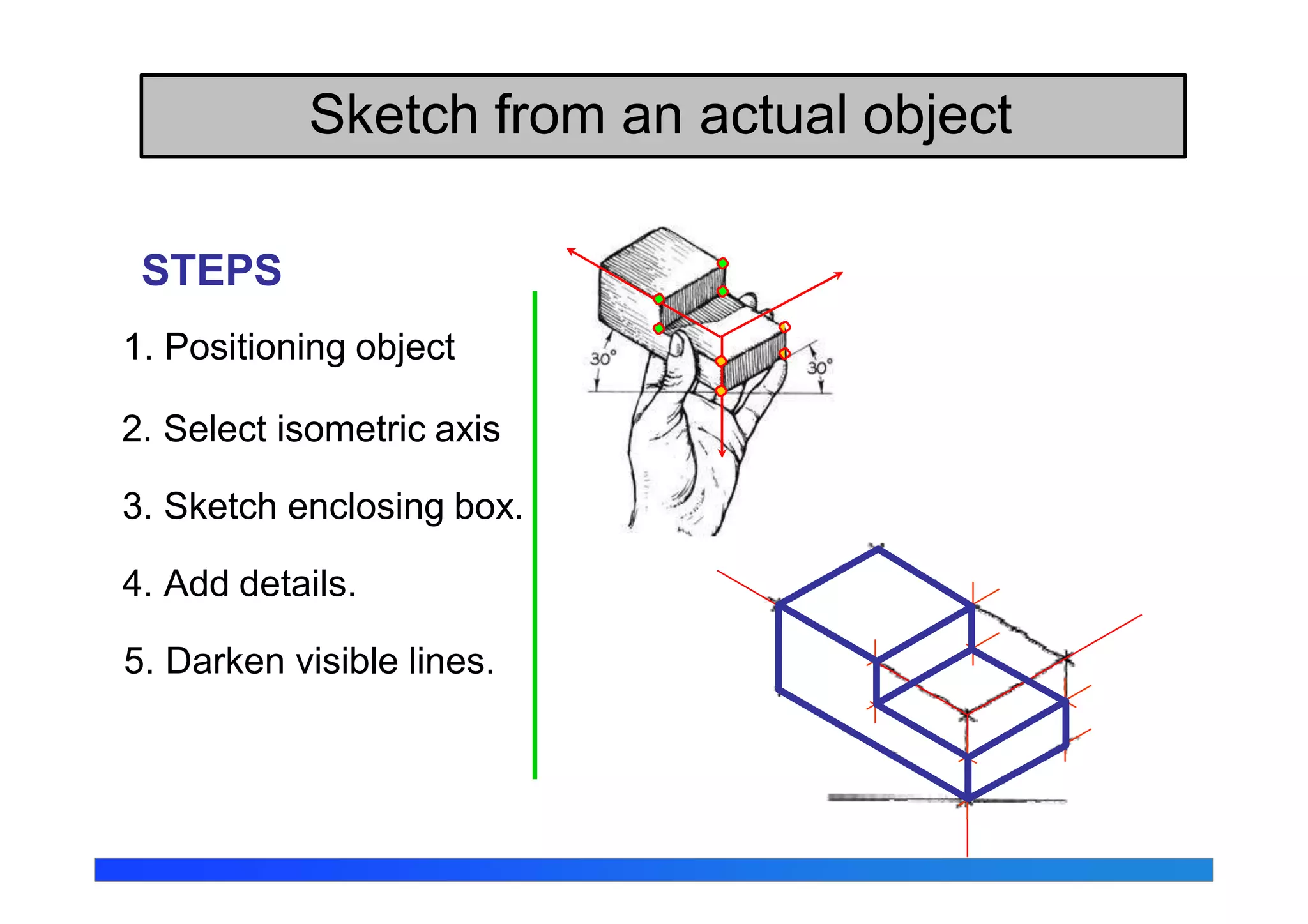
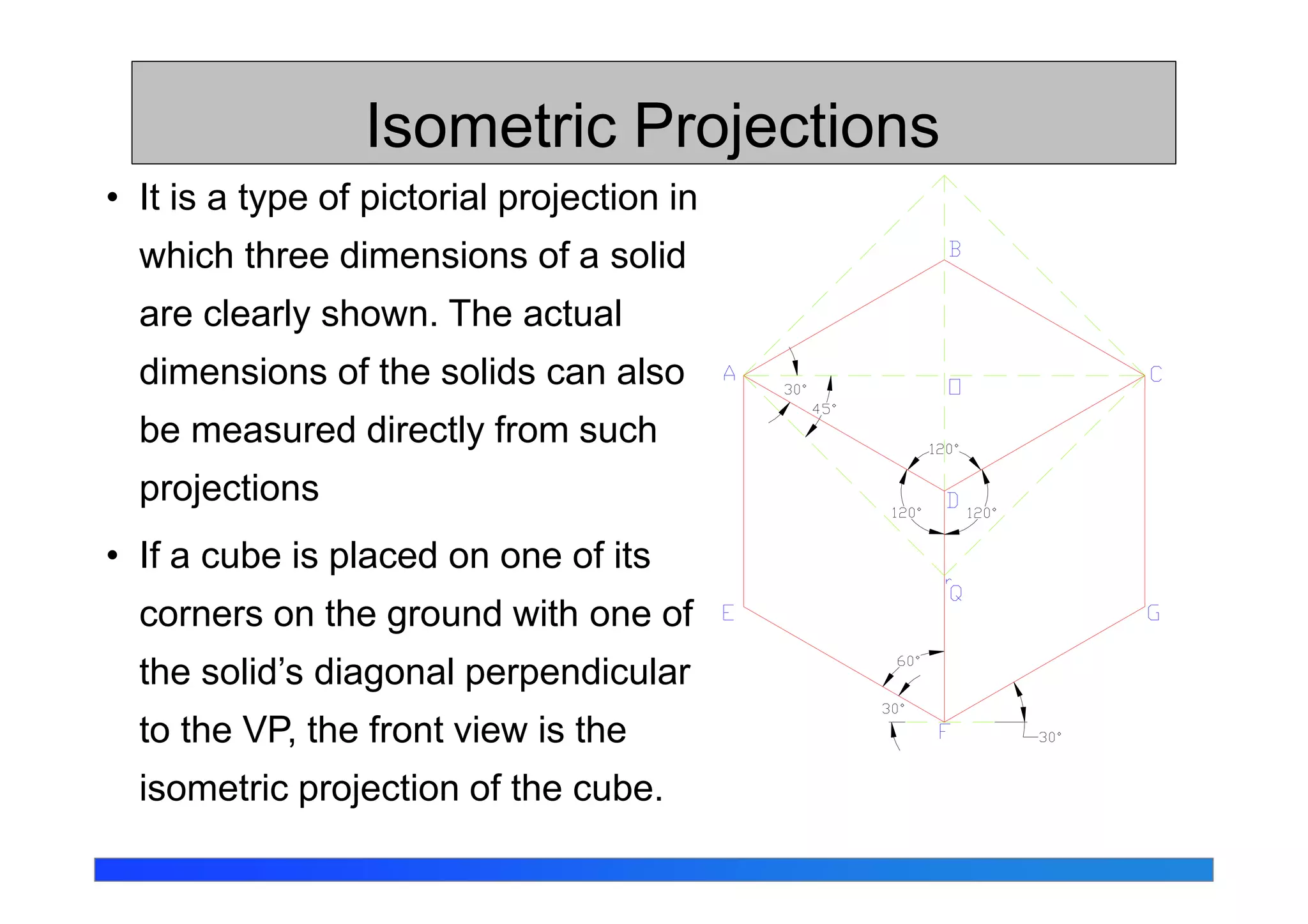
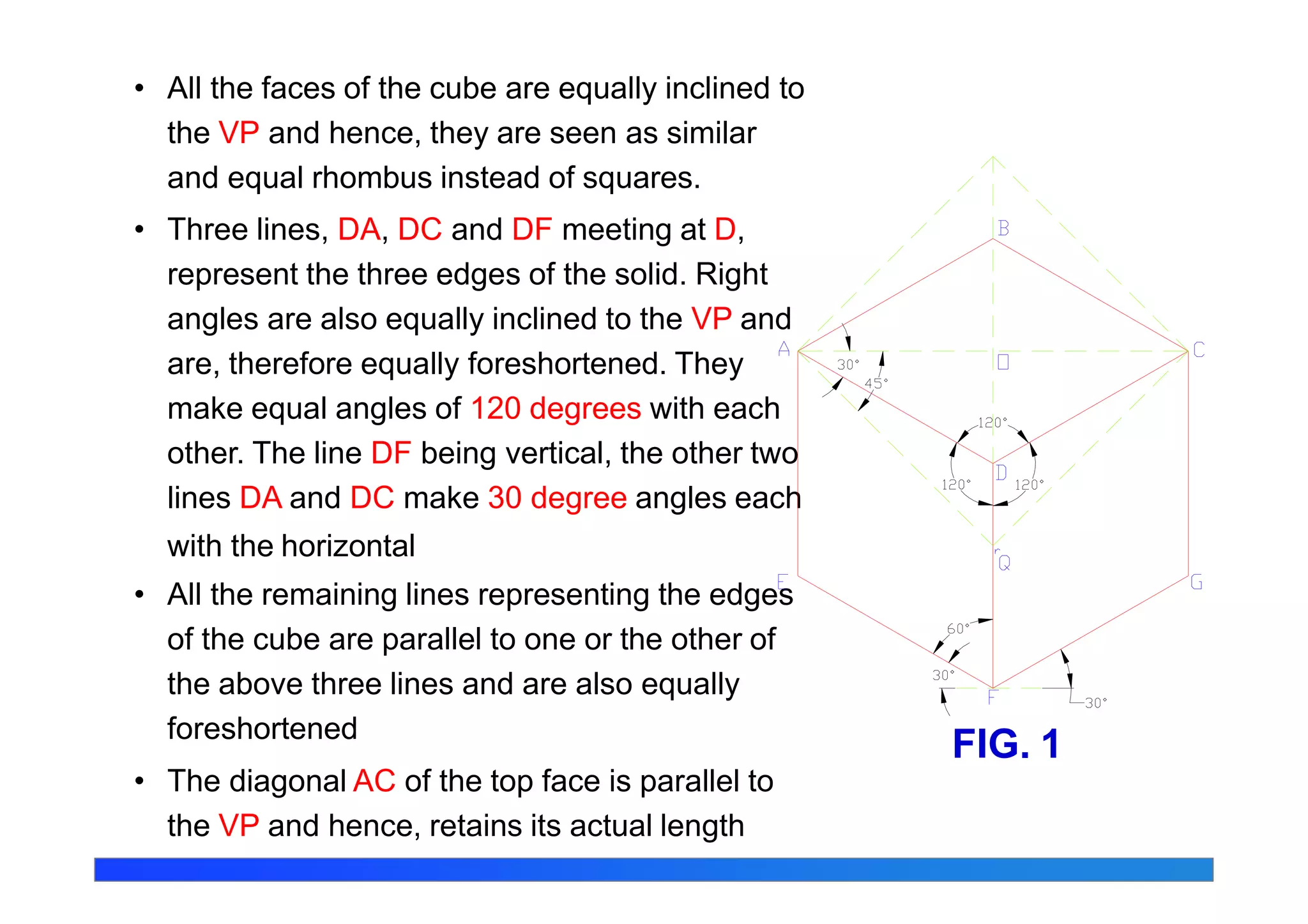
This document discusses isometric projections and drawings. It defines the different types of axonometric projections including isometric, dimetric, and trimetric. Isometric projections have all angles equal, while dimetric has two equal angles and trimetric has none equal. The document explains how to construct isometric scales and draw isometric views using true lengths rather than foreshortened lengths. It also covers orienting the isometric axes and the steps for sketching objects in isometric views.

1. Civil Engineering Drawing
Session 2015

2. C
A
D
B
Axonometric Projection
Type of axonometric drawing
a
b c
2. Dimetric Two angles are equal
b
a
c
3. Trimetric None of angles are
equal.
a
b c
1. Isometric All angles are equal
A
B
C
D
Axonometric axis
Sana Khan
UG-CE-2012 24/12/12
Axonometric axis
Axonometric axis

3. Isometric Projections
• It is a type of pictorial projection in
which three dimensions of a solid
are clearly shown. The actual
dimensions of the solids can also
be measured directly from such
projections
• If a cube is placed on one of its
corners on the ground with one of
the solid’s diagonal perpendicular
to the VP, the front view is the
isometric projection of the cube.

4. • All the faces of the cube are equally inclined to
the VP and hence, they are seen as similar
and equal rhombus instead of squares.
• Three lines, DA, DC and DF meeting at D,
represent the three edges of the solid. Right
angles are also equally inclined to the VP and
are, therefore equally foreshortened. They
make equal angles of 120 degrees with each
other. The line DF being vertical, the other two
lines DA and DC make 30 degree angles each
with the horizontal
• All the remaining lines representing the edges
of the cube are parallel to one or the other of
the above three lines and are also equally
foreshortened
• The diagonal AC of the top face is parallel to
the VP and hence, retains its actual length
FIG. 1

5. Isometric Axes, Lines and Planes
DA, DC and DF lines, meeting at
point D and subtending 120 degree
angles with each other are termed
as Isometric axes. All the lines
parallel to these axes are known as
isometric lines. The planes
representing the faces of the cubes
shown in Fig. 1 as well as other
planes parallel to these planes are
called isometric planes. In Fig.1.
EF, FG, FA, GC are examples of
Isometric lines, where faces ABCD,
ADFE, DFGC etc. are the examples
of Isometric planes
FIG. 1

6. Isometric scale
• As all the edges of the cube shown
in Fig. 1 have been equally
foreshortened the square faces
looks like rhombus. The rhombus
(i.e. ABCD) AC diagonal maintains
the true length of the diagonal
• Construct a square AQCP on
diagonal AC. AQ and AP are the
true lengths of the sides of the
square face, AD and AB are the
isometric lengths of sides AC and
AQ respectively FIG. 1

7. Isometric scale……contd
FIG. 1
UG-C

8. Isometric scale
• Thus isometric projection is reduced in the ratio ✓2:✓3
i.e. isometric lengths are 0.815 of the true length.
• Thus while drawing an isometric projection; it is essential
to convert true lengths into isometric lengths for
measuring and marking the sizes. This can easily be
done by constructing and making use of an isometric
scale.

9. Isometric scale
Draw a horizontal line BC of any length [fig. 2]. At the end B, draw
lines BA and BP making angles of 30 degree and 45 degree
respectively with BC. On line BP, mark divisions of true length. From
each division point on BP, draw vertical lines on BC. The vertical
lines will cut also cut the lines BA. The points thus obtained on line
BA give lengths on isometric scale.

10. Isometric scale….contd
The same scale can drawn with divisions of natural scale on
horizontal line BP [fig. 3]. From the ends B and P, draw lines BA and
PA making 15 degree and 45 degree angles with BP respectively,
and intersecting each other at point A. From division points of true
length on BP, draw lines parallel to PA and meeting BA at respective
points. The division along BA give dimensions on Isometric scales.
UG-CE-2014555 1

12. Isometric Drawing or Isometric View
• If the foreshortening of the isometric
lines in an isometric projection is
disregarded and instead, the true
lengths are marked, the view obtained
will be exactly of the same shape but
larger in proportion (about 22.5%) than
that obtained by the use of isometric
scale.
• Due to the ease in construction and the
advantage of measuring the dimensions
directly from the drawing, it has become
a general practice to use the true scale
instead of the isometric scale.
• To avoid confusion, the view drawn with
the true scale is called isometric drawing
or isometric view, whilethat drawn with
the use of isometric scale is called
isometric projection.

13. Isometric Drawing or Isometric View
• in isometric view of any
rectangular solid resting on a
face on the ground, each
horizontal face will have its
sides parallel to the two sloping
axes.

14. Isometric Drawing or Isometric View
• Each vertical face will have its sides parallel to
the vertical axis and the other sides parallel to
one of the sloping axes.
• In other words, the vertical edgesi.e. shown
by vertical lines, while the horizontal edges are
represented by lines,making 30 degree
angles with the horizontal. These lines are
very conveniently drawn with the T-square and
a 30-60 degreeset square

15. Isometric sketch
Isometric sketch is an isometric view that is drawn
in full size.
Isometric projection
(True projection)
Isometric drawing
(Full size)
Forshorten
Full scale

16. Orientation of Isometric Axes
Isometric axes can be arbitrarily oriented to create
different views of a single object.
Regular
isometric
Reverse axis
isometric
Long axis
isometric
View point is looking
down on the top of
the object.
View point is looking
up on the bottom of
the object.
View point is looking
from the right (or left)
of the object.

17. UG-CE-2012 24/12/12 Sana Khan
Isometric
Sketching

18. 1. Place the object in the position which its shape
and features are clearly seen.
2. Define an isometric axis.
3. Sketching the enclosing box (or cylinder).
4. Estimate the size an and relationship of each
details.
5. Darken all visible lines.
Sketch from an actual object

19. STEPS
1. Positioning object
2. Select isometric axis
3. Sketch enclosing box.
4. Add details.
5. Darken visible lines.
Sketch from an actual object

20. Note In isometric sketch/drawing), hidden lines are omitted
unless they are absolutely necessary.
STEPS
1. Positioning object.
2. Select isometric axis.
3. Sketch enclosing
box.
4. Add details.
5. Darken visible lines.
Sketch from an actual object