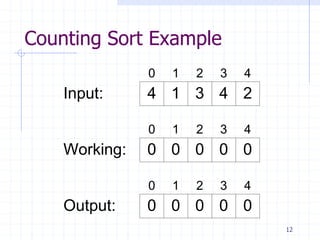
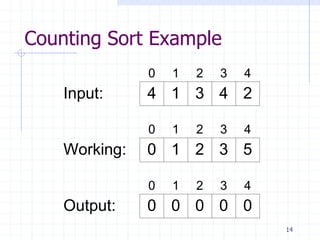
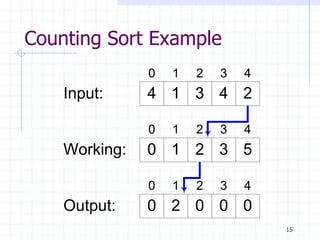
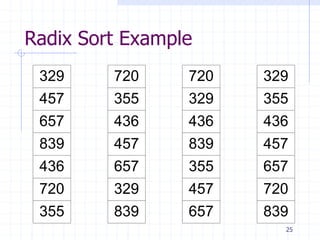
1. Counting sort and radix sort can sort in linear time O(n) by exploiting properties of the input rather than just comparisons. Counting sort assumes integers as input and radix sort assumes digitized numbers. 2. Bucket sort also runs in linear time if inputs are uniformly distributed between 0 and 1. It divides the range into buckets and distributes inputs into the corresponding buckets which are then sorted. 3. The comparison-based lower bound of Ω(nlogn) does not apply to these algorithms because they do not rely solely on comparisons. Counting sort counts occurrences rather than comparing, and radix/bucket sort distribute into buckets based on digits/positions rather than comparisons.

1. 1
Data Structures & Algorithms
Sorting in Linear Time

2. 2
Lower bounds for sorting
The sorting algorithms we’ve looked at
so far are all comparison sorts
 Comparison sorts all have lower bound of
O(nlgn), as we’ve seen
 Why?
 Assume for simplicity that elements in a given
set are distinct, so we only need to worry about
< and > operations

3. 3
The Decision-Tree Model
Decision trees represent the comparisons
performed by a sorting algorithm
a1
: a2
a2
: a3
a1
: a3
<1, 2, 3> a1
: a3
<1, 3, 2> <3, 1, 2>
<2, 1, 3> a2
: a3
<2, 3, 1> <3, 2, 1>
<=<=
<= >
<= >
>
>
><=
<=

4. 4
The Decision-Tree Model
Internal nodes represent a particular
comparison
 Annotated by ai : aj for some i and j < n
Leaf nodes represent a particular permutation
of the input
Execution of the algorithm is analogous to
following a path through the decision tree
 Each possible permutation must appear as one of
the leaves of the tree for the sorting algorithm to
work properly

5. 5
Worst Case Lower Bound
The height of the decision tree
represents the worst-case number of
comparisons the sorting algorithm
performs
 This is the same as a lower bound for the
running time of the algorithm
 Theorem 9.1 in the book states that any
decision tree that sorts n elements has
height of at least nlog2n

6. 6
Proof of Worst Case Lower
Bound
How many permutations of n elements are
there? n!
 All permutations must appear on the decision tree
The decision tree is binary in nature, so n!
<= 2h, where 2h is the maximum number of
leaves in the tree
 This means that h >= log2(n!)
 Chapter 2.11 has something called Stirling’s
approximation that states that n! > (n/e)n, where
e = 2.71828…, the base of natural logarithms

7. 7
Proof of Worst Case Lower
Bound
h >= log2(n/e)n
h = nlog2n – nlog2e (by log definition)
 which is O(nlog2n) (lower bound)
Since heapsort and mergesort have
upper bounds equal to the theoretical
lower bounds, they are called
asymptotically optimal sorts

8. 8
Sorting In Linear Time
It is possible to sort in linear time using
something other than a comparison sort
 However, this requires us to make
assumptions or have some foreknowledge
of the input

9. 9
Counting sort
Assumes that each of the n input
elements is an integer in the range 1 to
k, for some integer k
When k = O(n), the sort runs in O(n)
time

10. 10
Counting Sort
The idea of counting sort is to determine for
each input element x, the number of
elements < x
 We use this to position x directly into the output
array
 If all inputs aren’t distinct, we’ll have to modify
the algorithm somewhat
Three arrays are required: an input array, an
output, and a temporary working storage of
size k

11. 11
Counting Sort
void CountingSort(int Input[], int Output[], int size,
int max)
{
int Work[max] = { 0 }, index;
// Set Work[i] equal to the # elements = i
for ( index = 0 ; index < size ; ++ index )
Work[Input[index]] = Work[Input[index]] + 1;
// Now set each Work[i] equal to # elements <= i
for ( index = 2 ; index < max ; ++ index )
Work[index] = Work[index]+Work[index-1];
// Arrange the input into the output array
for ( index = size-1 ; index >= 0 ; --index )
{
--Work[Input[index]]; // Handles non-distinct input
Output[Work[Input[index]]] = Input[index];
}
}

12. 12
Counting Sort Example
4 1 3 4 2Input:
Working:
0 1 2 3 4
0 0 0 0 0
0 1 2 3 4
Output: 0 0 0 0 0
0 1 2 3 4

13. 13
Counting Sort Example
4 1 3 4 2Input:
Working:
0 1 2 3 4
0 1 1 1 2
0 1 2 3 4
Output: 0 0 0 0 0
0 1 2 3 4

14. 14
Counting Sort Example
4 1 3 4 2Input:
Working:
0 1 2 3 4
0 1 2 3 5
0 1 2 3 4
Output: 0 0 0 0 0
0 1 2 3 4

15. 15
Counting Sort Example
4 1 3 4 2Input:
Working:
0 1 2 3 4
0 1 2 3 5
0 1 2 3 4
Output: 0 2 0 0 0
0 1 2 3 4

16. 16
Counting Sort Example
4 1 3 4 2Input:
Working:
0 1 2 3 4
0 1 1 3 5
0 1 2 3 4
Output: 0 2 0 0 4
0 1 2 3 4

17. 17
Counting Sort Example
4 1 3 4 2Input:
Working:
0 1 2 3 4
0 1 1 3 4
0 1 2 3 4
Output: 0 2 3 0 4
0 1 2 3 4

18. 18
Counting Sort Example
4 1 3 4 2Input:
Working:
0 1 2 3 4
0 1 1 2 4
0 1 2 3 4
Output: 1 2 3 0 4
0 1 2 3 4

19. 19
Counting Sort Example
4 1 3 4 2Input:
Working:
0 1 2 3 4
0 0 1 2 4
0 1 2 3 4
Output: 1 2 3 4 4
0 1 2 3 4

20. 20
Analysis of Counting Sort
How much time does this take?
 Initialization takes O(max) time
 Each loop takes O(n) time
 Total running time is O(max) + 3*O(n) = O(max
+ n)
Note that as the max approaches n, our
running time approaches O(n)
Why doesn’t the comparison-sort lower
bound apply?

21. 21
Counting Sort
Counting Sort is considered to be a
stable sort
 Ties between non-distinct elements are
resolved by keeping the order of values in
the output array the same as they were in
the input array
 This is important if we have “satellite” data
When is the Counting Sort practical?

22. 22
Radix sort
Radix Sort was developed to be used by
card sorting machines
 Cards were sorted into 80 columns, each
with 12 holes that could be punched
 A d-digit number occupied d-columns
 The machines could only look at one
column at a time, and had only twelve bins
How can the cards be sorted?

23. 23
Radix Sort
An intuitive approach would be to sort
on the most-significant digit, then sort
each bin recursively
 Since these were physical bins, that wasn’t
an option (you only had twelve, one for
each punched hole)

24. 24
Radix Sort
Radix Sort follows this algorithm:
1. The cards are sorted into bins based on
the least significant digit first;
2. The cards are combined into a single
deck;
3. The cards are sorted on the next most
significant digit;
4. Repeat 2 & 3 as necessary
Requires d passes through the deck

25. 25
Radix Sort Example
329
457
657
839
436
720
355
720
355
436
457
657
329
839
720
329
436
839
355
457
657
329
355
436
457
657
720
839

26. 26
Radix Sort
Radix Sort requires the per-digit sort to
be stable
In modern computers, a radix-sort
might be used to achieve sorts on
multiple keys
 E.g., by last name, date, and sales figures

27. 27
Radix Sort Algorithm
void RadixSort(ArrayType Input[], int size, int digits)
{
for ( int i = 0 ; i < digits ; ++i )
// perform stable sort on Input using digit i
}

28. 28
Analysis of Radix Sort
How does radix sort compare?
 Running time is O(d*n + d*max)
 If d is constant, and max = O(n), radix sort
runs in O(n) time.

29. 29
Bucket sort
This is another sorting algorithm that
can perform in linear time
 It also requires you to make an assumption
about the input
 Assumption: the input is generated by a
random process that distributes the
elements uniformly over the interval [0, 1)

30. 30
Bucket Sort
Here’s the basic algorithm:
 Divide the interval into n equal-sized subintervals,
or buckets
 Distribute the n input numbers into the buckets
 We don’t expect many numbers to fall into each bucket,
but we must handle for > 1 in each bucket
 Each bucket is therefore a linked list
 Sort each bucket
 Iterate across the buckets in order, collecting all of
the elements

31. 31
Bucket Sort Algorithm
void BucketSort(double Input[], int size)
{
list<double> buckets[size];
for ( int idx = 0 ; idx < size ; ++idx )
buckets[n*Input[idx]].insert(Input[idx]);
for ( int idx = 0 ; idx < size ; ++idx )
insertion_sort(buckets[idx]);
// concatenate all buckets
}

32. 32
Bucket Sort Example
0.78 0.17 0.39 0.26 0.72 0.94 0.21 0.12 0.23 0.68Input:
Buckets: null
null
null
null
0
1
2
3
4
5
6
7
8
9
0.78
0.17
0.39
0.26
0.72
0.94
0.21
0.12
0.23
0.68
null
null
null
null
null
null

33. 33
Bucket Sort Example
0.78 0.17 0.39 0.26 0.72 0.94 0.21 0.12 0.23 0.68Input:
Buckets: null
null
null
null
0
1
2
3
4
5
6
7
8
9
0.72
0.12
0.39
0.21
0.78
0.94
0.23
0.17
0.26
0.68
null
null
null
null
null
null

34. 34
Bucket Sort Example
Output:
Buckets: null
null
null
null
0
1
2
3
4
5
6
7
8
9
0.72
0.12
0.39
0.21
0.78
0.94
0.23
0.17
0.26
0.68
null
null
null
null
null
null
0.12 0.17 0.21 0.23 0.26 0.39 0.68 0.72 0.78 0.94

35. 35
Bucket Sort
We can eliminate the insertion sort step
by using a sorted list, that keeps its
elements sorted through insertions, etc.
 This does not significantly change the
running time
 Read through the example on your own;
the math is complicated, but comes out
like this: as the distribution becomes more
uniform, the running time gets more linear