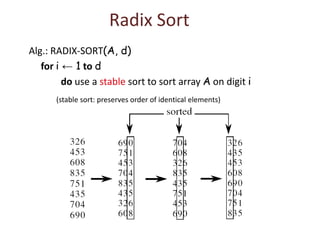
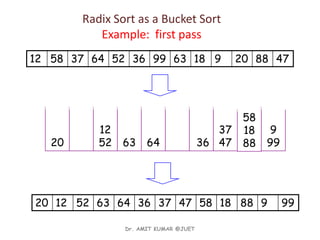
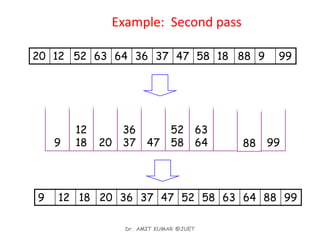
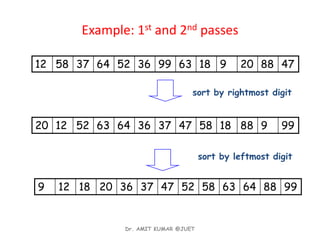
Linear sorting algorithms like counting sort, bucket sort, and radix sort can sort arrays of numbers in linear O(n) time by exploiting properties of the data. Counting sort works for integers within a range [0,r] by counting the frequency of each number and using the frequencies to place numbers in the correct output positions. Bucket sort places numbers uniformly distributed between 0 and 1 into buckets and sorts the buckets. Radix sort treats multi-digit numbers as strings by sorting based on individual digit positions from least to most significant.

1. Linear Sorting
Sorting in O(N) time
Dr. AMIT KUMAR @JUET

2. How Fast Can We Sort?
• Selection Sort, Bubble Sort, Insertion Sort:
• Heap Sort, Merge sort:
• Quicksort:
• What is common to all these algorithms?
– Make comparisons between input elements
ai < aj, ai ≤ aj, ai = aj, ai ≥ aj, or ai > aj
O(n2)
O(nlgn)
O(nlgn) - average

3. Can we do better than O( n log n )?
– No.
– It can be proven that any comparison-based sorting
algorithm will need to carry out at least O( n log n )
operations
How Fast Can We Sort?
Dr. AMIT KUMAR @JUET

4. Can we do better?
• Linear sorting algorithms
– Bucket sort
– Radix Sort
– Counting Sort
• Make certain assumptions about the data
• Linear sorts are NOT “comparison sorts”

5. Restrictions on the problem
• Suppose the values in the list to be sorted can
repeat but the values have a limit (e.g., values
are digits from 0 to 9)
• Sorting, in this case, appears easier.
• Is it possible to come up with an algorithm
better than O( n log n )?
– Yes
– Strategy will not involve comparisons
Dr. AMIT KUMAR @JUET

6. Bucket Sort
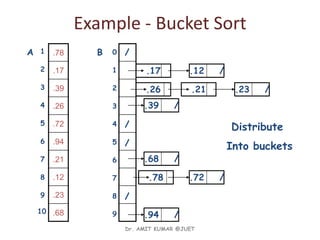
• Assumption:
– the input is generated by a random process that distributes elements
uniformly over [0, 1]
• Idea:
– Divide [(0, 1) into k equal-sized buckets (k=Θ(n))]
– Distribute the n input values into the buckets
– Sort each bucket (e.g., using quicksort)
– Go through the buckets in order, listing elements in each one
• Input: A[1 . . n], where 0 ≤ A[i] < 1 for all i
• Output: elements A[i] sorted
Dr. AMIT KUMAR @JUET

7. Example - Bucket Sort
Dr. AMIT KUMAR @JUET

8. Example - Bucket Sort
.78
.17
.39
.26
.72
.94
.21
.12
.23
.68
0
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
10
.21
.12 /
.72 /
.23 /
.78
.94 /
.68 /
.39 /
.26
.17
/
/
/
/
A B
Distribute
Into buckets
Dr. AMIT KUMAR @JUET

9. Example - Bucket Sort
0
1
2
3
4
5
6
7
8
9
.23
.17 /
.78 /
.26 /
.72
.94 /
.68 /
.39 /
.21
.12
/
/
/
/
Sort within each
bucket
Dr. AMIT KUMAR @JUET

10. Example - Bucket Sort
0
1
2
3
4
5
6
7
8
9
.23
.17 /
.78 /
.26 /
.72
.94 /
.68 /
.39 /
.21
.12
/
/
/
/
.17.12 .23 .26.21 .39 .68 .78.72 .94 /
Concatenate the lists from
0 to n – 1 together, in order
Dr. AMIT KUMAR @JUET

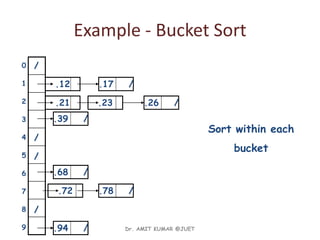
11. Bucket sort algorithm
Algorithm BucketSort( S )
( values in S are between 0 and m-1 )
for j  0 to m-1 do // initialize m buckets
b[j]  0
for i  0 to n-1 do // place elements in their
b[S[i]]  b[S[i]] + 1 // appropriate buckets
i  0
for j  0 to m-1 do // place elements in buckets
for r  1 to b[j] do // back in S
S[i]  j
i  i + 1
Dr. AMIT KUMAR @JUET

12. Time complexity
• Bucket initialization: O( m )
• From array to buckets: O( n )
• From buckets to array: O( n )
– Even though this stage is a nested loop, notice that all we
do is dequeue from each bucket until they are all empty –>
n dequeue operations in all
• Since m will likely be small compared to n, Bucket
sort is O( n )
– Strictly speaking, time complexity is O ( n + m )
Dr. AMIT KUMAR @JUET

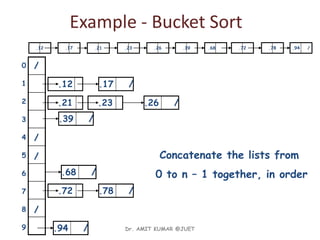
13. Analysis of Bucket Sort
Alg.: BUCKET-SORT(A, n)
for i ← 1 to n
do insert A[i] into list B[nA[i]]
for i ← 0 to k - 1
do sort list B[i] with quicksort sort
concatenate lists B[0], B[1], . . . , B[n -1]
together in order
return the concatenated lists
O(n)
k O(n/k log(n/k))
=O(nlog(n/k)
O(k)
O(n) (if k=Θ(n))
Dr. AMIT KUMAR @JUET

14. Sorting integers
• Can we perform bucket sort on any array of (non-
negative) integers?
– Yes, but note that the number of buckets will depend on
the maximum integer value
• If you are sorting 1000 integers and the maximum
value is 999999, you will need 1 million buckets!
– Time complexity is not really O( n ) because m is much >
than n. Actual time complexity is O( m )
• Can we do better?
Dr. AMIT KUMAR @JUET

15. Radix Sort
• Represents keys as d-digit numbers in some base-k
key = x1x2...xd where 0≤xi≤k-1
• Example: key=15
key10 = 15, d=2, k=10 where 0≤xi≤9
key2 = 1111, d=4, k=2 where 0≤xi≤1
Dr. AMIT KUMAR @JUET

16. Radix Sort
• Assumptions
d=O(1) and k =O(n)
• Sorting looks at one column at a time
– For a d digit number, sort the least significant
digit first
– Continue sorting on the next least significant
digit, until all digits have been sorted
– Requires only d passes through the list
Dr. AMIT KUMAR @JUET

17. Radix Sort
Alg.: RADIX-SORT(A, d)
for i ← 1 to d
do use a stable sort to sort array A on digit i
(stable sort: preserves order of identical elements)

18. Analysis of Radix Sort
• Given n numbers of d digits each, where each digit may take
up to k possible values, RADIX-SORT correctly sorts the
numbers in O(d(n+k))
– One pass of sorting per digit takes O(n+k) assuming that
we use counting sort
– There are d passes (for each digit)
Dr. AMIT KUMAR @JUET

19. Analysis of Radix Sort
• Given n numbers of d digits each, where each digit may take
up to k possible values, RADIX-SORT correctly sorts the
numbers in O(d(n+k))
– Assuming d=O(1) and k=O(n), running time is O(n)
Dr. AMIT KUMAR @JUET

20. Radix Sort as a Bucket Sort
Example: first pass
12 58 37 64 52 36 99 63 18 9 20 88 47
20
12
52 63 64 36
37
47
58
18
88
9
99
20 12 52 63 64 36 37 47 58 18 88 9 99
Dr. AMIT KUMAR @JUET

21. Example: Second pass
9 12 18 20 36 37 47 52 58 63 64 88 99
9
12
18 20
36
37 47
52
58
63
64 88 99
20 12 52 63 64 36 37 47 58 18 88 9 99
Dr. AMIT KUMAR @JUET

22. Example: 1st and 2nd passes
12 58 37 64 52 36 99 63 18 9 20 88 47
20 12 52 63 64 36 37 47 58 18 88 9 99
9 12 18 20 36 37 47 52 58 63 64 88 99
sort by rightmost digit
sort by leftmost digit
Dr. AMIT KUMAR @JUET

23. Radix Sort as a Bucket Sort
Dr. AMIT KUMAR @JUET

24. Radix sort and stability
• Radix sort works as long as the bucket sort stages are
stable sorts
• Stable sort: in case of ties, relative order of elements
are preserved in the resulting array
– Suppose there are two elements whose first digit is the
same; for example, 52 & 58
– If 52 occurs before 58 in the array prior to the sorting
stage, 52 should occur before 58 in the resulting array
• This way, the work carried out in the previous bucket
sort stages is preserved
Dr. AMIT KUMAR @JUET

25. About Radix sort
• Note that only 10 buckets are needed
regardless of number of stages since the
buckets are reused at each stage
• Radix sort can apply to words
– Set a limit to the number of letters in a word
– Use 27 buckets (or more, depending on the
letters/characters allowed), one for each letter
plus a “blank” character
– The word-length limit is exactly the number of
bucket sort stages needed
Dr. AMIT KUMAR @JUET

26. Counting Sort
• Assumptions:
– n integers which are in the range [0 ... r]
– r is in the order of n, that is, r=O(n)
• Idea:
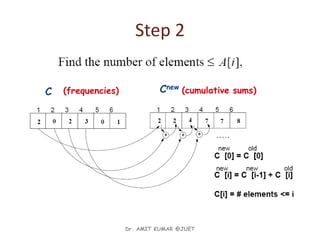
– For each element x, find the number of elements x
– Place x into its correct position in the output array
output array
Dr. AMIT KUMAR @JUET

27. Step 1
(i.e., frequencies)
(r=6)
Dr. AMIT KUMAR @JUET

28. Step 2
Cnew
C (frequencies) (cumulative sums)
Dr. AMIT KUMAR @JUET

29. Algorithm
• Start from the last element of A
• Place A[i] at its correct place in the output array
• Decrease C[A[i]] by one
30320352
1 2 3 4 5 6 7 8
A
77422
1 2 3 4 5
Cnew 8
0
Dr. AMIT KUMAR @JUET

30. Example
30320352
1 2 3 4 5 6 7 8
A 77422
1 2 3 4 5
Cnew 8
0
3
1 2 3 4 5 6 7 8
B
76422
1 2 3 4 5
Cnew 8
0
30
1 2 3 4 5 6 7 8
B
76421
1 2 3 4 5
Cnew
8
0
330
1 2 3 4 5 6 7 8
B
75421
1 2 3 4 5
Cnew
8
0
3320
1 2 3 4 5 6 7 8
B
75321
1 2 3 4 5
Cnew
8
0
Dr. AMIT KUMAR @JUET

31. Example (cont.)
30320352
1 2 3 4 5 6 7 8
A
33200
1 2 3 4 5 6 7 8
B
75320
1 2 3 4 5
C 8
0
5333200
1 2 3 4 5 6 7 8
B
74320
1 2 3 4 5
C 7
0
333200
1 2 3 4 5 6 7 8
B
74320
1 2 3 4 5
C 8
0
53332200
1 2 3 4 5 6 7 8
B
Dr. AMIT KUMAR @JUET

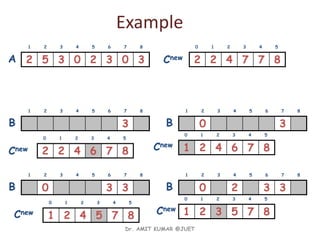
32. COUNTING-SORT ALGO
Alg.: COUNTING-SORT(A, B, n, k)
1. for i ← 0 to r
2. do C[ i ] ← 0
3. for j ← 1 to n
4. do C[A[ j ]] ← C[A[ j ]] + 1
5. C[i] contains the number of elements equal to i
6. for i ← 1 to r
7. do C[ i ] ← C[ i ] + C[i -1]
8. C[i] contains the number of elements ≤ i
9. for j ← n downto 1
10. do B[C[A[ j ]]] ← A[ j ]
11. C[A[ j ]] ← C[A[ j ]] - 1
1 n
0 k
A
C
1 n
B
j

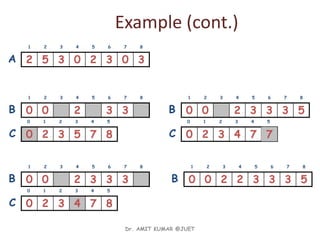
33. Analysis of Counting Sort
Alg.: COUNTING-SORT(A, B, n, k)
1. for i ← 0 to r
2. do C[ i ] ← 0
3. for j ← 1 to n
4. do C[A[ j ]] ← C[A[ j ]] + 1
5. C[i] contains the number of elements equal to i
6. for i ← 1 to r
7. do C[ i ] ← C[ i ] + C[i -1]
8. C[i] contains the number of elements ≤ i
9. for j ← n downto 1
10. do B[C[A[ j ]]] ← A[ j ]
11. C[A[ j ]] ← C[A[ j ]] - 1
O(r)
O(n)
O(r)
O(n)
Overall time: O(n + r)

34. Analysis of Counting Sort
• Overall time: O(n + r)
• In practice we use COUNTING sort when r =
O(n)
 running time is O(n)
Dr. AMIT KUMAR @JUET

35. Dr. AMIT KUMAR @JUET