This document discusses algorithms for sorting and searching data structures. It introduces binary search, which can search an ordered array in O(log n) time by recursively searching either the left or right half of the array. Quicksort is also discussed, which works by recursively sorting partitions of the array around a pivot element. In the average case, quicksort runs in O(n log n) time, but in the worst case of an already sorted array it runs in O(n^2) time. The document covers methods for solving algorithm recurrences like substitution, iteration, and the master method, and applies these techniques to analyze the time complexity of binary search and quicksort.

1. Solving Recurrences and the QuickSort Algorithm 1
Advanced Data Structures &
Algorithm Design
Solving Recurrences and the QuickSort
Algorithm

2. Solving Recurrences and the QuickSort Algorith2
The Search Problem
 A complement to the sorting problem
discussed last week is the searching
problem:
 Given a set of elements A = {a1, a2, …, an} and a
search parameter s, return the location i of s in A
 If A is an ordered set, then the binary search
algorithm can be used to search A for some value

3. Solving Recurrences and the QuickSort Algorith3
The Binary Search Algorithm
 The binary search algorithm operates as
follows (where A is the input set, and mid is
the index of the element at the midpoint of A):
 If s = Amid, return mid
 If s < Amid, search the left half of A
 If s > Amid, search the right half of A

4. Solving Recurrences and the QuickSort Algorith4
The Binary Search Algorithm
int BinarySearch(const DataType A[], int first, int
last, const DataType &s)
{
if ( last < first ) return –1; // not found
int mid = (first + last) / 2;
if ( s == A[mid] ) return mid;
if ( s < A[mid] ) // search left
return BinarySearch(A, first, mid-1, s);
else
return BinarySearch(A, mid+1, last, s);
}
int BinarySearch(const DataType A[], int first, int
last, const DataType &s)
{
if ( last < first ) return –1; // not found
int mid = (first + last) / 2;
if ( s == A[mid] ) return mid;
if ( s < A[mid] ) // search left
return BinarySearch(A, first, mid-1, s);
else
return BinarySearch(A, mid+1, last, s);
}
What is the order of growth of the running time of
BinarySearch?
What is the order of growth of the running time of
BinarySearch?

5. Solving Recurrences and the QuickSort Algorith5
Analysis of Binary Search
 Each execution requires up to 4 constant
operations and 1 recursive function call that
operates on ½ the array, so:



>+
≤
=
1if)1()2/(
1if)1(
)(
nOnT
nO
nT
 We shall see tonight that this equates to
T(n)=O(log2n)

6. Solving Recurrences and the QuickSort Algorith6
Solving Recurrences
 Recall our recurrence relation from last week:



>+
=
=
1if)()2/(2
1if)1(
)(
nnOnT
nO
nT
 How do we solve this recurrence to
determine the actual running time?

7. Solving Recurrences and the QuickSort Algorith7
Solving Recurrences
 There are three methods that we can use:
 The Substitution Method
 We guess a bound, then use mathematical induction to
prove our guess is correct
 The Iteration Method
 Converts the recurrence into a summation, then relies
on techniques for bounding summations
 The Master Method
 Provides bounds for recurrences of the form
T(n)=aT(n/b)+f(n) utilizing a set of rules

8. Solving Recurrences and the QuickSort Algorith8
The Substitution Method
 Involves guessing the form of the solution,
then using mathematical induction to find the
constants and show that the solution works
 Can only be applied in cases when it is easy
to guess the form of the answer

9. Solving Recurrences and the QuickSort Algorith9
The Substitution Method: An Example
 We can guess that the solution is of the form
T(n)=O(nlog2n)
 By definition, this means that T(n) has some
upper bound of cnlog2n for some constant c > 0
 We’ll use induction to prove that this bound holds



>+
=
=
1if)2/(2
1if)1(
)(
nnnT
nO
nT

10. Solving Recurrences and the QuickSort Algorith10
The Substitution Method: An Example
1aslongas-log
log
2loglog
)2/(log
))2/(log]2/[(2)(
:yieldsrecurrencetheintothisngSubstituti
)2/(log)2/()2/(
:isthat,2/forholdsboundthat thisassumingbystartWe
2
2
22
2
2
2
≥≤
+−=
+−=
+≤
+≤
≤
cncn
ncnncn
ncnncn
nncn
nnncnT
nncnT
n

11. Solving Recurrences and the QuickSort Algorith11
The Substitution Method: An Example
 Now we must show that our solution holds for
the boundary conditions
 This means that we must be able to show that we
can choose the constant c to be large enough so
that the bound holds for all n, including the
boundary conditions
 For example, assume that our only boundary
condition is that T(1)=1
 With our solution, T(1) <= c1log21 = 0, no matter
what c is

12. Solving Recurrences and the QuickSort Algorith12
The Substitution Method: An Example
 This problem can normally be easily
overcome
 Asymptotic notation only requires us to prove that
T(n)<=cnlog2n for some n >= n0
 We can choose n0 to remove the difficult boundary
condition from consideration
 E.g., choosing n0 to be 2 or 3 removes the difficult
boundary of 1 from consideration

13. Solving Recurrences and the QuickSort Algorith13
The Iteration Method
 No guesses are required, but significant
algebra is
 The idea is to expand the recurrence and
express it as a summation of terms
dependent only on n

14. Solving Recurrences and the QuickSort Algorith14
The Iteration Method: An Example
)64/(27)16/(9)4/(3
)))64/(3)16/((3)4/((3
))16/(3)4/((3
)4/(3)(
:followsasititeratecanWe
:)4/(3)(recurrenceheConsider t
nTnnn
nTnnn
nTnn
nTnnT
nnTnT
+++=
+++=
++=
+=
+=
How much iteration is enough?How much iteration is enough?

15. Solving Recurrences and the QuickSort Algorith15
The Iteration Method: An Example
 The i-th term in the series is 3i
(n/4i
)
 This iteration hits n=1 when (n/4i
)=1 or when
i>log4n
 If we continue the iteration to this point, we
discover a decreasing geometric series:
)(
)(4
2.9)(identity)(
4
3
)1(3...64/2716/94/3)(
0
3log
log
4
4
nO
nOn
nn
nnnnnT
i
i
n
=
+=
Θ+





≤
Θ+++++≤
∑
∞
=

16. Solving Recurrences and the QuickSort Algorith16
The Iteration Method
 There are two important points to focus on
when utilizing the Iteration Method:
 How many times must the recurrence be iterated
to reach the boundary condition?
 What is the summation of the terms?
 The book describes a technique called
“recurrence trees”, which are helpful in
finding a solution

17. Solving Recurrences and the QuickSort Algorith17
The Master Method
 Provides a “cookbook” approach to solving
recurrences
 It is used specifically to solve recurrences of the
form T(n)=aT(n/b)+cnk
 Recurrences of this form describe solutions that divide
problems into subproblems of size n/b, where cnk
is the
cost of dividing the problem and combining the results

18. Solving Recurrences and the QuickSort Algorith18
The Master Method
 To use the master method, you must
memorize three case:





<
=
>
=
k
k
k
k
k
a
ba
ba
ba
nO
nnO
nO
nT
b
if
if
if
)(
)log(
)(
)(
log
 Note that these are simplified versions of the
solutions found in the book

19. Solving Recurrences and the QuickSort Algorith19
QuickSort
 QuickSort is a typical example of a divide-
and-conquer algorithm:
 Divide – partitions the input around an arbitrary
element
 Conquer – sorts each partition
 Combine – sorting is performed in-place, and so
requires zero work
 The algorithm consists of two functions, the
recursive QuickSort(), which utilizes
Partition() to divide the array

20. Solving Recurrences and the QuickSort Algorith20
QuickSort
void QuickSort(ArrayType &A, int begin, int end)
{
if ( begin < end )
{
int q = Partition(A, begin, end);
QuickSort(A, begin, q-1);
QuickSort(A, q+1, end);
}
}
void QuickSort(ArrayType &A, int begin, int end)
{
if ( begin < end )
{
int q = Partition(A, begin, end);
QuickSort(A, begin, q-1);
QuickSort(A, q+1, end);
}
}

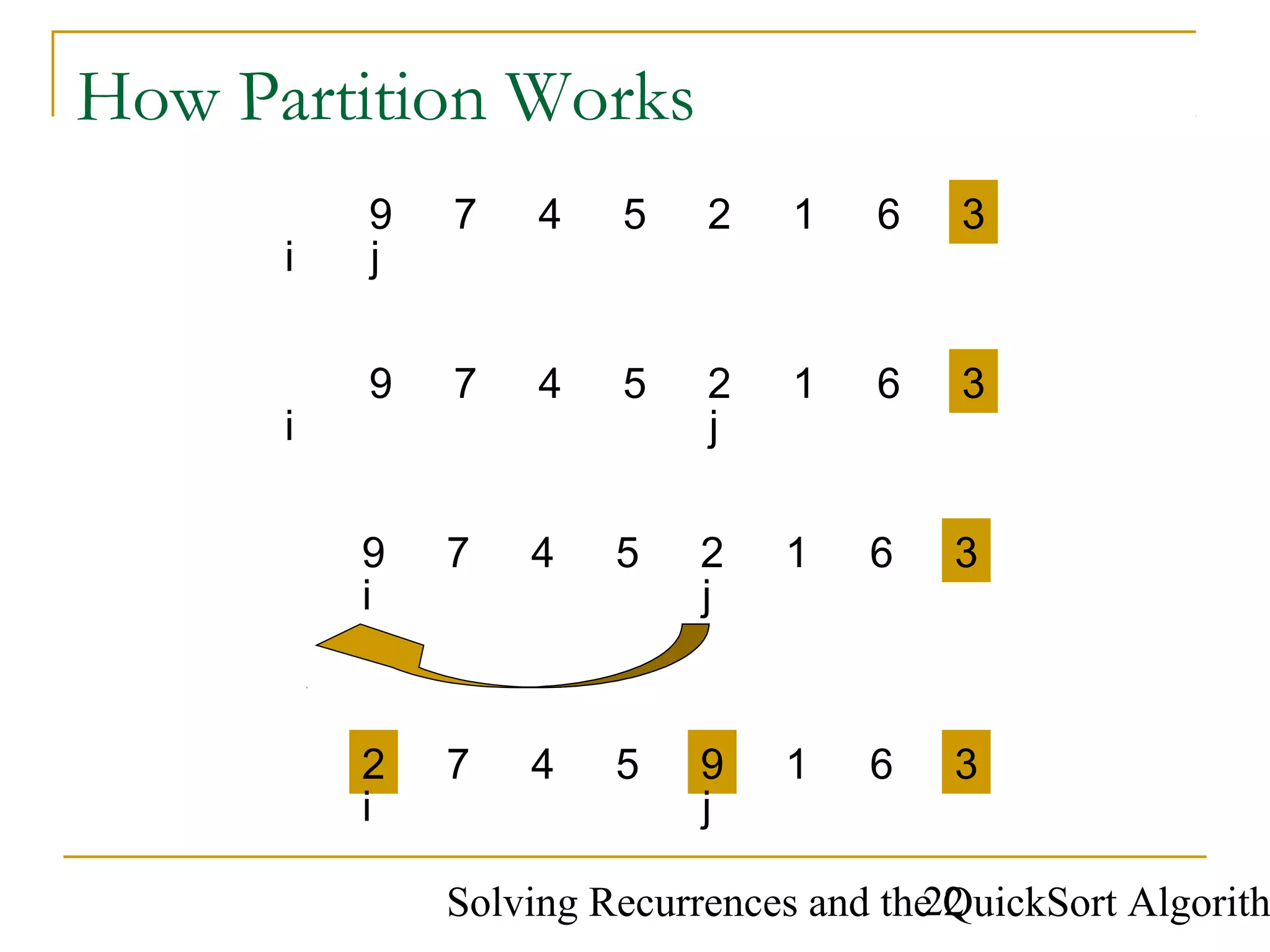
21. Solving Recurrences and the QuickSort Algorith21
QuickSort: Partition
int Partition(ArrayType A[], int begin, int end)
{
ArrayType x = A[end];
int i = begin - 1;
for ( int j = begin ; j < end ; ++j )
{
if ( A[j] < x )
{
++i;
swap(A[i], A[j]);
}
}
swap(A[i+1], A[end]);
return i+1;
}
int Partition(ArrayType A[], int begin, int end)
{
ArrayType x = A[end];
int i = begin - 1;
for ( int j = begin ; j < end ; ++j )
{
if ( A[j] < x )
{
++i;
swap(A[i], A[j]);
}
}
swap(A[i+1], A[end]);
return i+1;
}

22. Solving Recurrences and the QuickSort Algorith22
How Partition Works
9 7 4 5 2 1 6 3
i j
9 7 4 5 2 1 6 3
i j
9 7 4 5 2 1 6 3
i j
97 4 52 1 6 3
i j

23. Solving Recurrences and the QuickSort Algorith23
How Partition Works
9 7 452 1 63
The final result of the first partitioning:
•The partition element is in it’s final sorted position
•QuickSort now operates on each subarray
independently

24. Solving Recurrences and the QuickSort Algorith24
Analysis of QuickSort
 In the best case, Partition() divides the array evenly
at every level
 Each problem is divided into two equal subproblems of size
n/2
 Partition() itself is O(n) (it has a single loop that executes
some number of times based on the size of the input)
 The recurrence then is T(n)=2T(n/2)+n
 Using the Master Method:
 a=2, bk
=21
=2, a=bk
 this is Case 2
 T(n)=O(nk
log2n)=O(n1
log2n)=O(nlog2n)

25. Solving Recurrences and the QuickSort Algorith25
Analysis of QuickSort
 In the worst case, the size of one partition is
1 and the other is n-1
 Observing that T(1)=O(1), then the worst-case
recurrence is:
 T(n)=T(n-1)+O(n)+O(1)
 T(n)=T(n-1)+O(n)

26. Solving Recurrences and the QuickSort Algorith26
Analysis of QuickSort
 When will this worst-
case occur?
 How likely will it
occur?
 Why does it occur?
 How can we
improve it?
)(
)(
)()1()(
:iterationusecanweHere
2
1
1
n
k
k
nnTnT
n
k
n
k
Θ=






Θ=
Θ=
Θ+−=
∑
∑
=
=

27. Solving Recurrences and the QuickSort Algorith27
Homework
 Reading: 4.1-4.3; 8.1-8.2; 8.4
 Exercises:
 4.3-1, 2, 3