Download to read offline
![We know found nodes are
reachable from s because we
have traced out a path.
If a node has been handled,
then all of its neighbors
have been found.
Graph Search
Exit
a
c
h
k
f
i
m
j
e
b
g
d
l
All found nodes are handled.
Exit Reachable nodes have been Found.
•Postconditions:
found = handled
handled
Notfound
[A ⇒ B] = [¬B ⇒ ¬A]
NotFound nodes not reachable.](https://image.slidesharecdn.com/5-searching-140325165958-phpapp02/85/5-searching-19-320.jpg)
Uploaded byashish bansal
5 searching
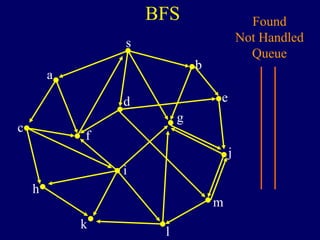
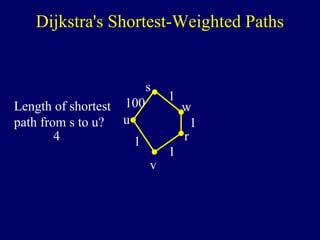
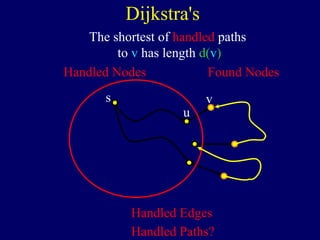
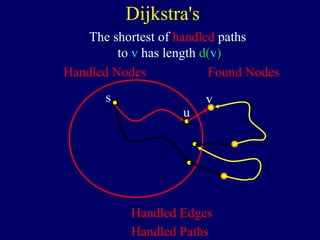
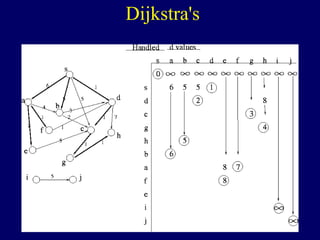
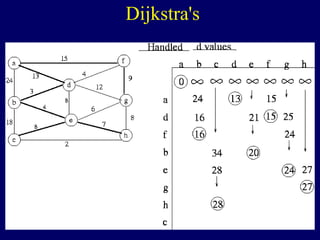
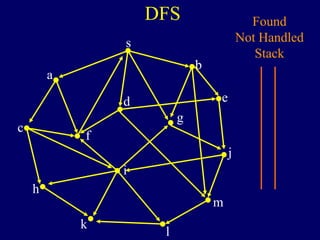
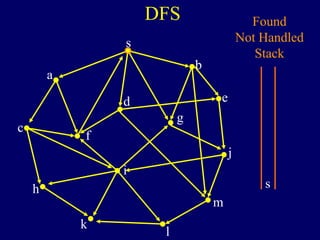
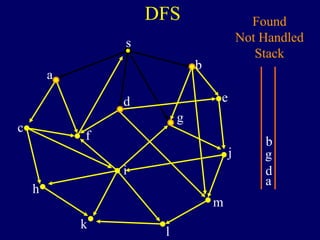
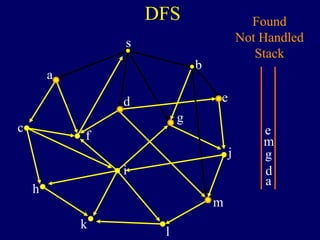
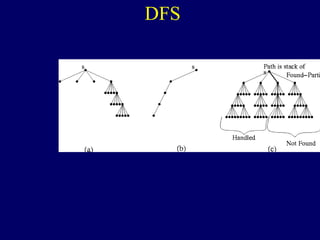
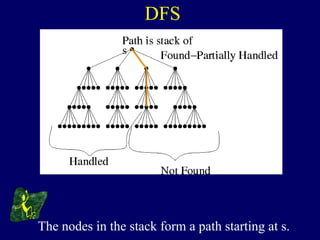
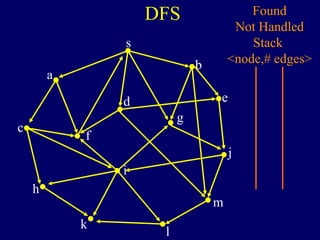
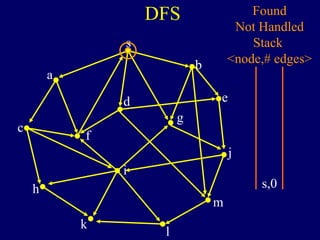
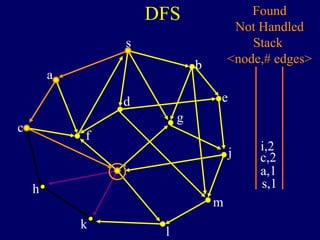
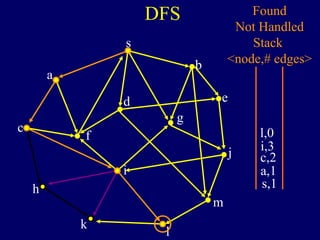
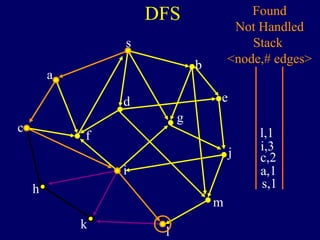
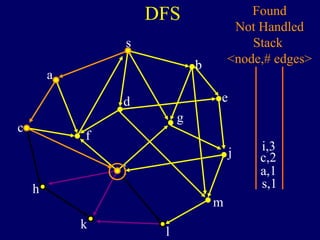
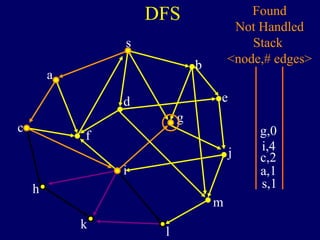
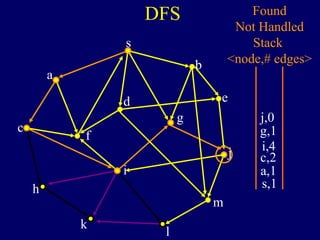
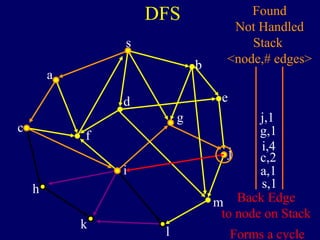
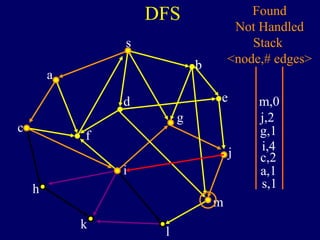
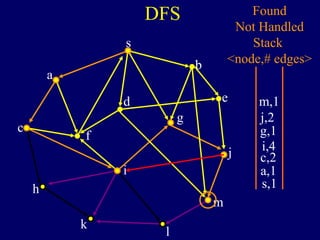
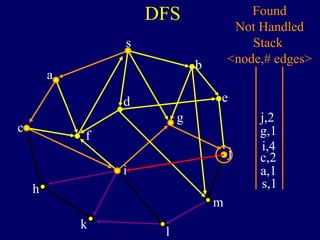
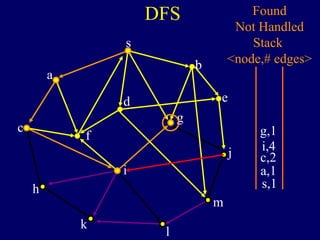
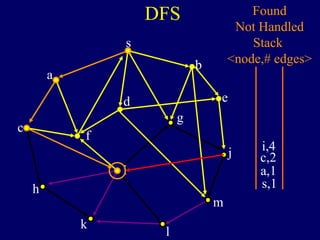
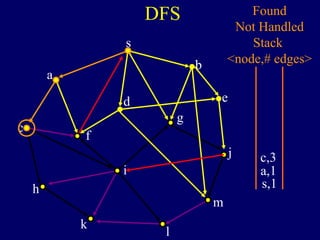
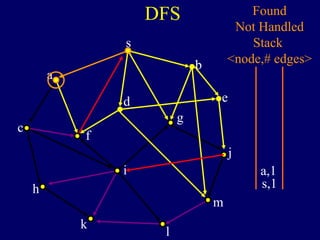
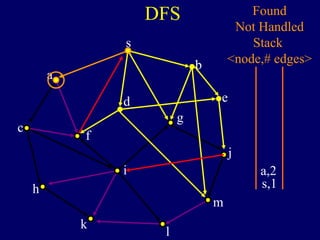
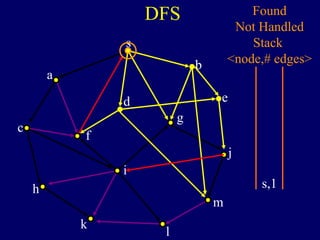
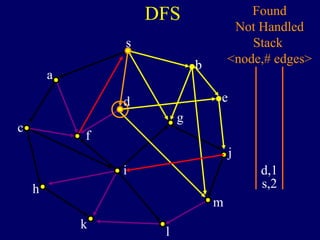
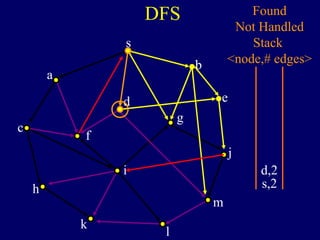
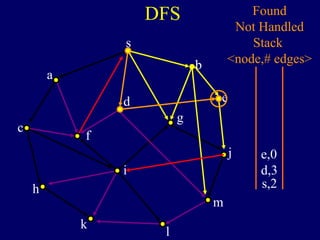
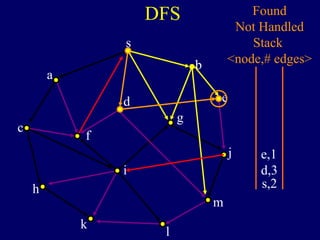
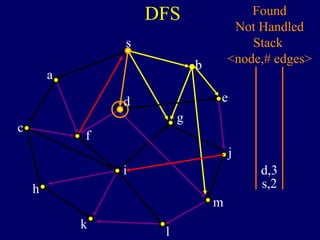
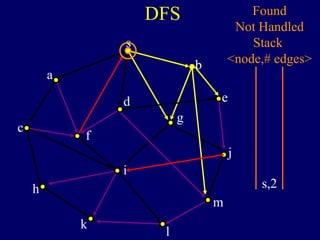
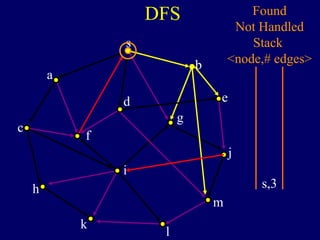
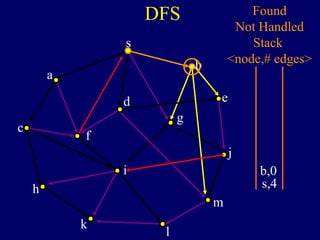
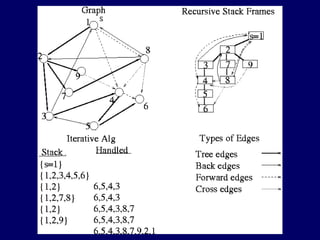
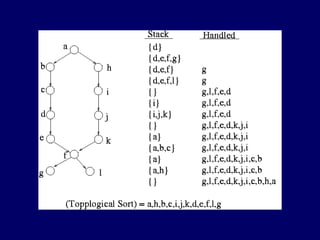
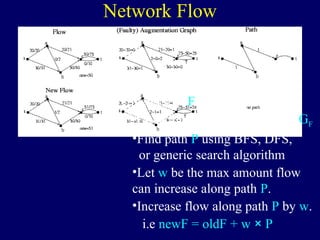
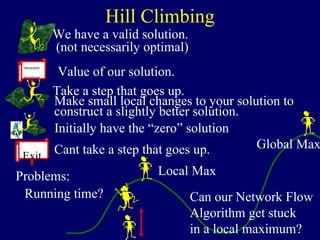
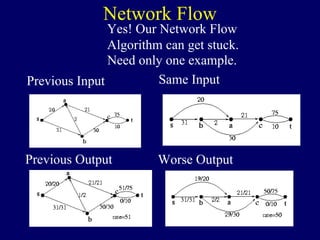
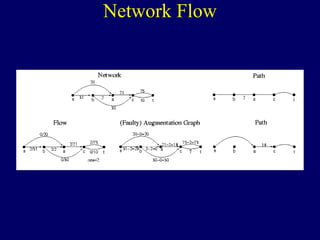
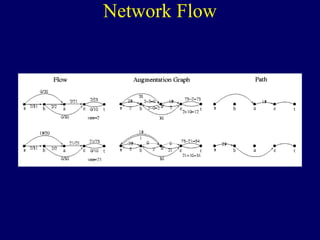
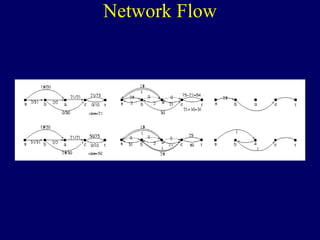
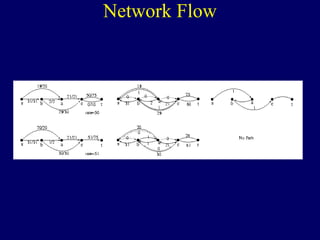
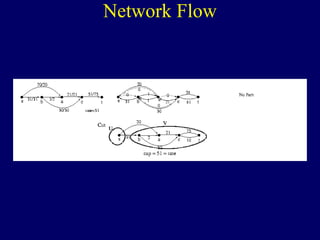
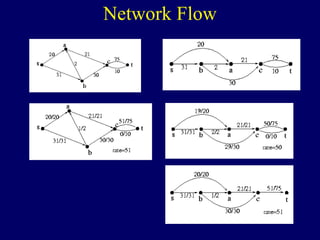
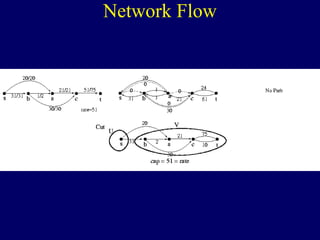
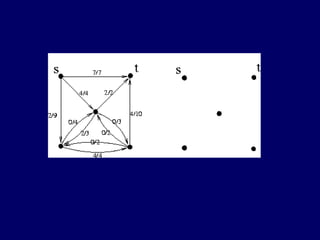
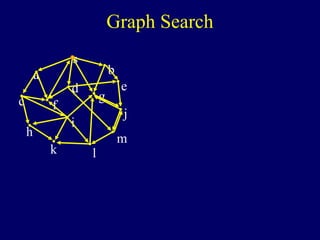
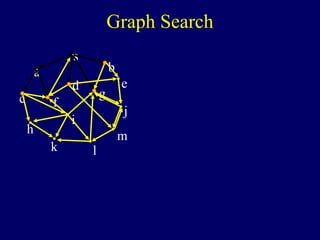
The document discusses graph search algorithms. It begins by defining the problem of finding all nodes reachable from a single source node s in a graph G. It then outlines the basic steps of a graph search: (1) start with the known reachable nodes as just s; (2) repeatedly find neighbors of known reachable nodes and add them as new reachable nodes; (3) terminate when no more progress can be made. 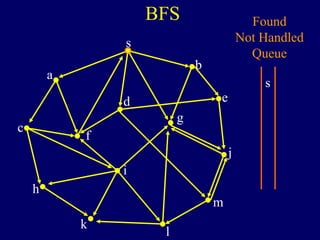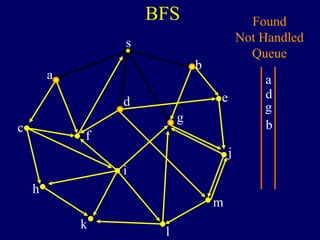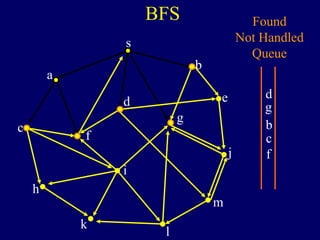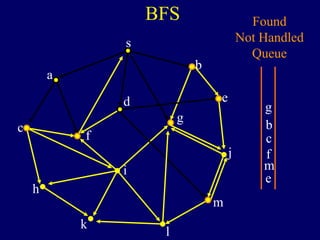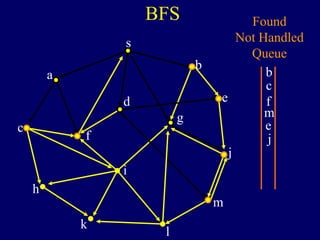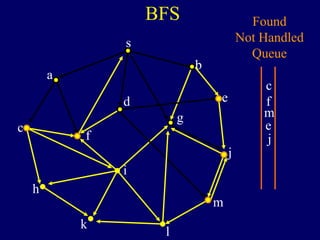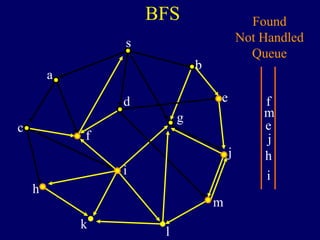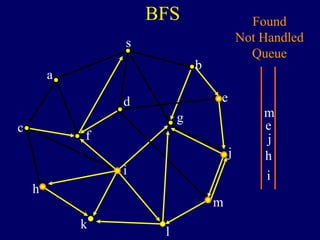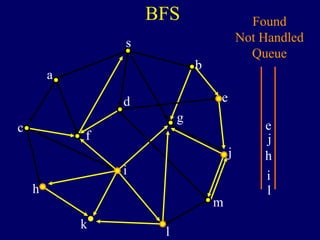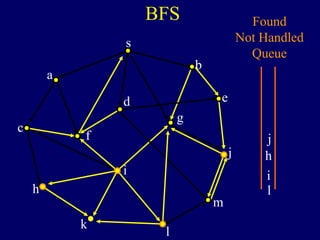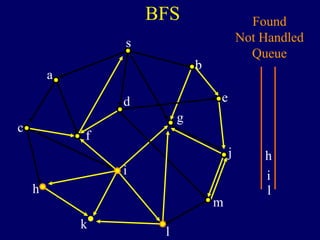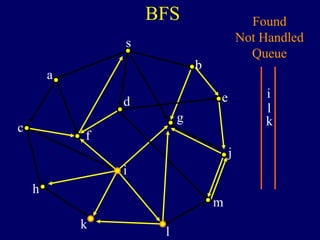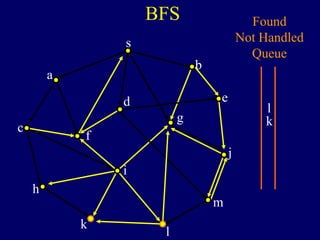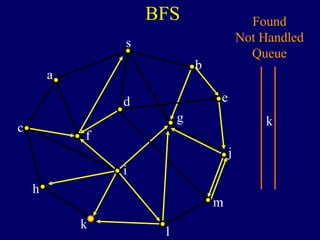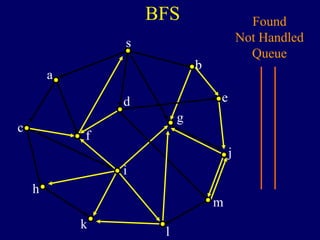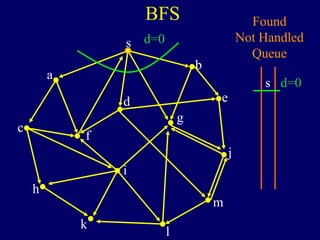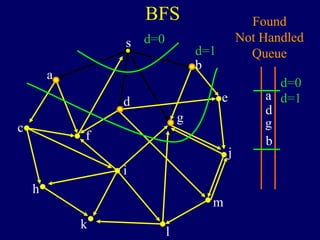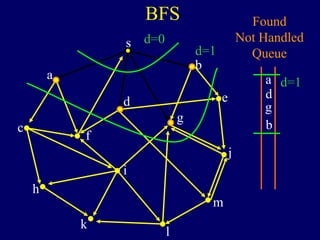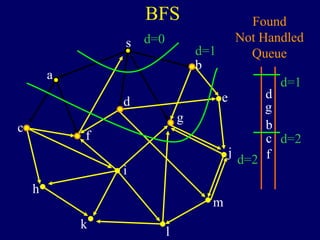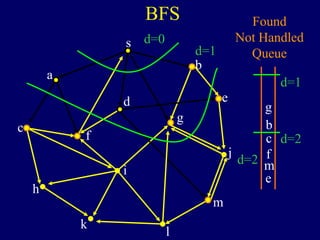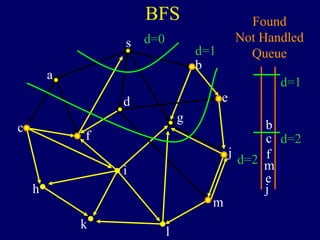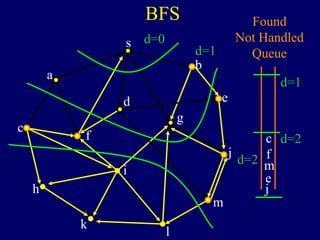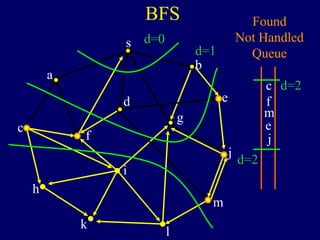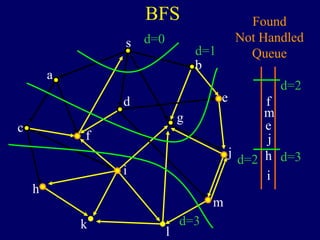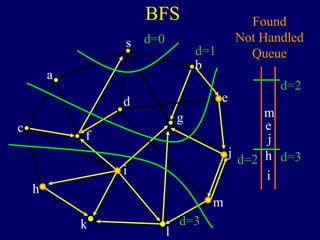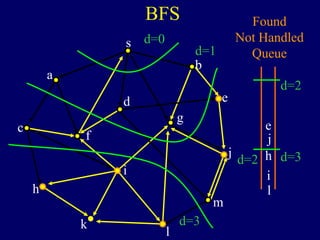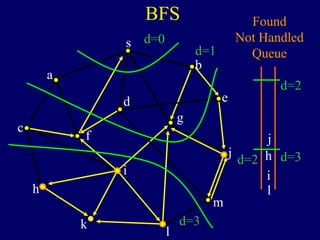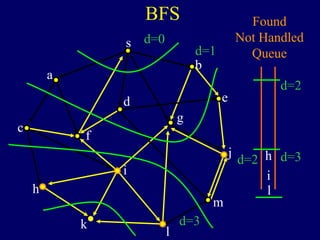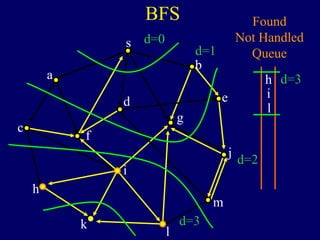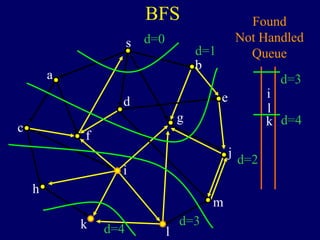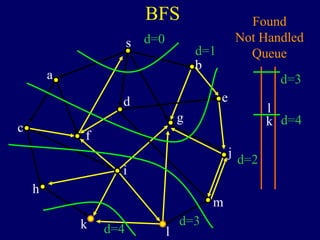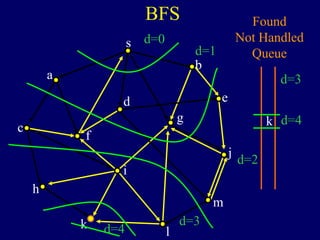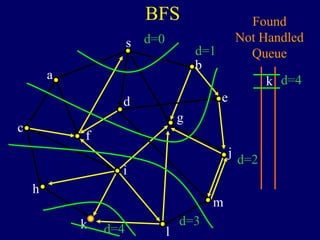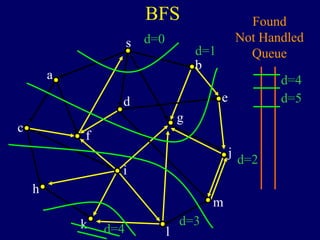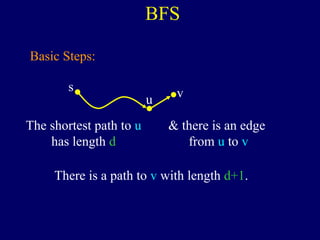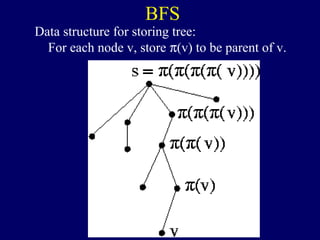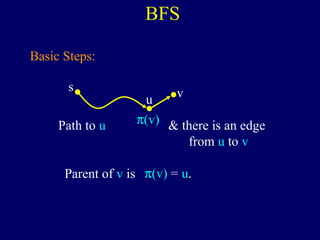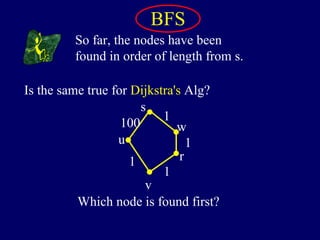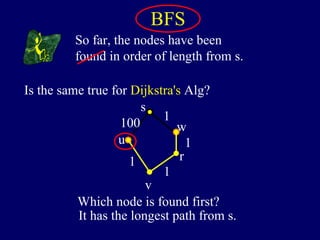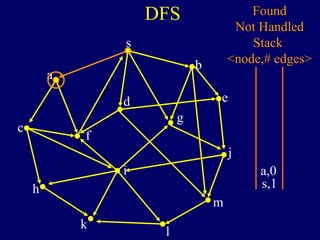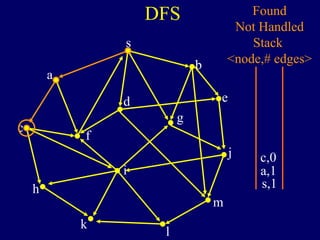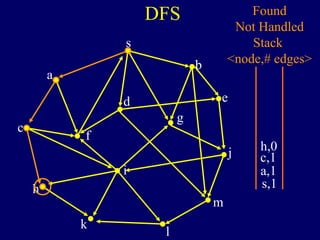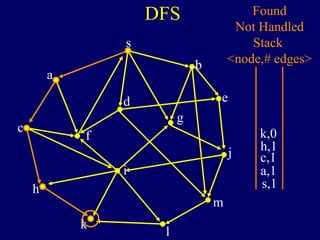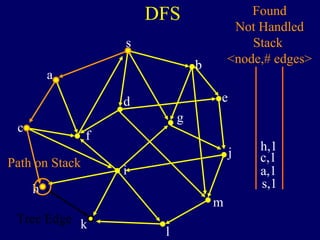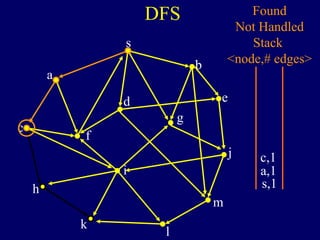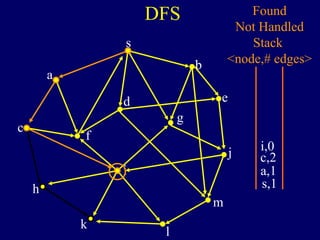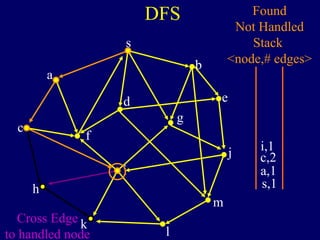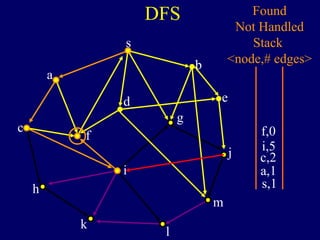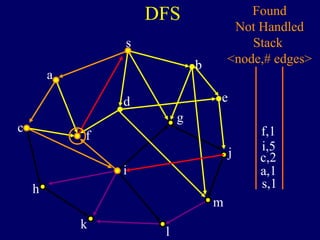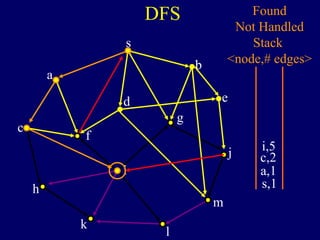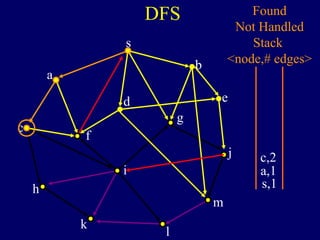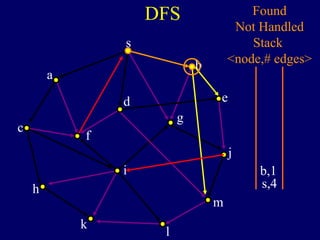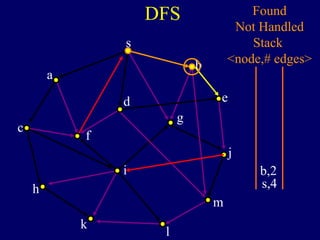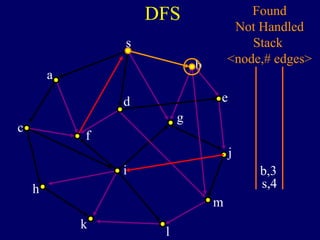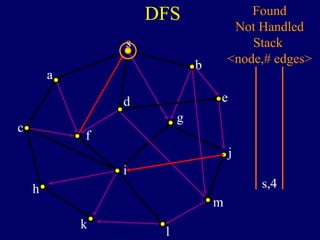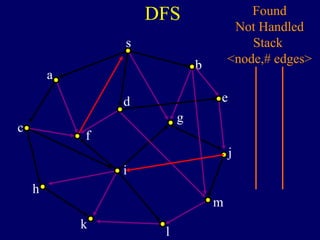It then describes breadth-first search (BFS) in detail, showing how BFS finds nodes in order of distance from s by maintaining a queue of found nodes not yet handled. At each step, BFS handles the next node in the queue, finds its neighbors, and adds them to the found
5 searching
- 1. Searching in aGraph Jeff Edmonds York University COSC 3101LectureLecture 55
- 2. Generic Search Breadth FirstSearch Dijkstra's Shortest Paths Algorithm Depth First Search Linear Order Network Flow Linear Programming
- 3. Graph a c b Node ~city or computer Edge ~ road or network Undirected or Directed A surprisingly large number of problems in computer science can be expressed as a graph theory problem.
- 4. Graph Search Specification: Reachability-from-single-sources •Preconditions: The input is a graph G (either directed or undirected) and a source node s. •Postconditions: Output all the nodes u that are reachable by a path in G from s.
- 5. Graph Search Basic Steps: s u Supposeyou know that u is reachable from s v & there is an edge from u to v You know that v is reachable from s Build up a set of reachable nodes.
- 6. Graph Search s reachable f u k reachable d v wreachable e h d reachable b t reachable d v w reachable e h d reachable b t •How do we keep track of all of this information? •How do we avoid cycling?
- 7.
- 8.
- 9.
- 10. s a c h k f i m j e b g d We know foundnodes are reachable from s because we have traced out a path. If a node has been handled, then all of its neighbors have been found. Graph Search l
- 11. s a c h k f i m j e b g d We know foundnodes are reachable from s because we have traced out a path. If a node has been handled, then all of its neighbors have been found. Graph Search l Handle some foundNotHandled node i.e. find its neighbors Don’t refind a node.
- 12. We know foundnodes are reachable from s because we have traced out a path. If a node has been handled, then all of its neighbors have been found. Graph Search Handle some foundNotHandled node i.e. find its neighbors s a c h k f i m j e b g d l
- 13. We know foundnodes are reachable from s because we have traced out a path. If a node has been handled, then all of its neighbors have been found. Graph Search # of found nodes. s a c h k f i m j e b g d l measure progress # of handled nodes. Might not increase.
- 14. We know foundnodes are reachable from s because we have traced out a path. If a node has been handled, then all of its neighbors have been found. Graph Search Node s is foundNotHandled s a c h k f i l m j e b g d Other nodes NotFound
- 15. We know foundnodes are reachable from s because we have traced out a path. If a node has been handled, then all of its neighbors have been found. Graph Search All nodes found. Exit a c h k f i m j e b g d l When can’t make any more progress. No. Might not find all. When all found nodes are have been handled. Handle some foundNotHandled node s
- 17. Graph Search We knowfound nodes are reachable from s because we have traced out a path. If a node has been handled, then all of its neighbors have been found. a c h k f i m j e b g d l Exit All found nodes are handled. Exit •Postconditions: Output all the nodes u that are reachable by a path in G from s. Output Found nodes
- 18. We know foundnodes are reachable from s because we have traced out a path. If a node has been handled, then all of its neighbors have been found. Graph Search Exit a c h k f i m j e b g d l All found nodes are handled. Exit Found nodes are reachable from s. Reachable nodes have been Found. •Postconditions:
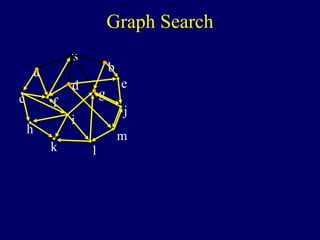
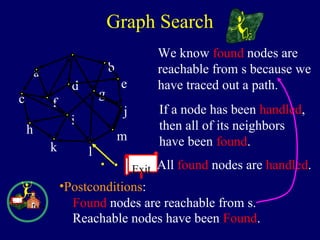
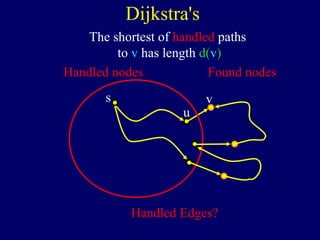
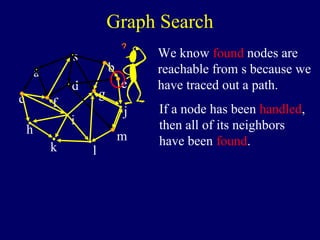
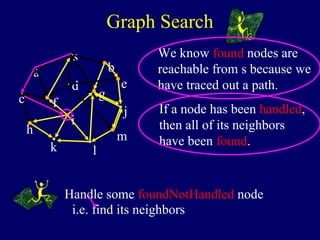
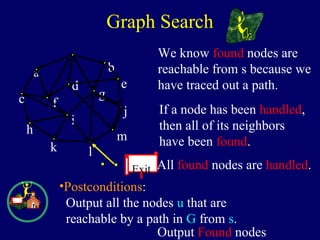
- 19. We know foundnodes are reachable from s because we have traced out a path. If a node has been handled, then all of its neighbors have been found. Graph Search Exit a c h k f i m j e b g d l All found nodes are handled. Exit Reachable nodes have been Found. •Postconditions: found = handled handled Notfound [A ⇒ B] = [¬B ⇒ ¬A] NotFound nodes not reachable.
- 20. Graph Search Specification ofReachability-from-single-source s •Preconditions: The input is a graph G (either directed or undirected) and a source node s. •Postconditions: Output all the nodes u that are reachable by a path in G from s. EndingInitial ConditionsMake Progress Maintain Loop InvDefine Exit ConditionDefine Step Define Measure of Progress Define Loop Invariants Define Problem km∞ 79 km to school Exit Exit 79 km 75 km Exit Exit 0 km Exit
- 21. Graph Search # ofhandled nodes. Handle some foundNotHandled node Time = O(n) f u k O(n) iterations, but iteration takes more than O(1) O(n) neighbors= O(n2 ) Could be fewer? Each edge visited, times.2 = O(E) Size = O(E) Linear time.
- 22. Graph Search Handle somefoundNotHandled node •Queue: Handle in order found. •Breadth-First Search •Stack: Handle most recently found •Depth-First Search •Priority Queue: Handle node that seems to be closest to s. •Shortest (Weighted) Paths:
- 23. Breadth First Search Pre& Post Conditions Algorithm
- 24.
- 25.
- 26.
- 27.
- 28.
- 29.
- 30.
- 31.
- 32.
- 33.
- 34.
- 35.
- 36.
- 37.
- 38.
- 39.
- 40. BFS What order arethe nodes found? i.e. Breadth First Search Algorithm So far, the nodes have been found in order of length from s.
- 41.
- 42.
- 43.
- 44.
- 45.
- 46.
- 47.
- 48.
- 49.
- 50.
- 51.
- 52.
- 53.
- 54.
- 55.
- 56.
- 57.
- 58.
- 59.
- 60.
- 61. BFS What order arethe nodes found? So far, the nodes have been found in order of length from s. Post Conditions: Finds a shortest path from s to each node v and its length. To prove path is shortest: Prove there is a path of this length. Prove there are no shorter paths. Give a path (witness)
- 62. Basic Steps: s u The shortestpath to u has length d v & there is an edge from u to v There is a path to v with length d+1. BFS
- 63. BFS What order arethe nodes found? So far, the nodes have been found in order of length from s. Post Conditions: Finds a shortest path from s to each node v and its length. When we find v, we know there isn't a shorter path to it because ? Prove there are no shorter paths. Otherwise, we would have found it already.
- 64. BFS Data structure forstoring tree: For each node v, store π(v) to be parent of v.
- 65. Basic Steps: s u Path tou v & there is an edge from u to v Parent of v is π(v) π(v) = u. BFS
- 67. Graph Search Handle somefoundNotHandled node •Queue: Handle in order found. •Breadth-First Search •Stack: Handle most recently found •Depth-First Search •Priority Queue: Handle node that seems to be closest to s. •Shortest (Weighted) Paths:
- 68. Dijkstra's Shortest-Weighted Paths Specification:Dijkstra's Shortest-Weighted Paths Reachability-from-single-source s •Preconditions: The input is a graph G (either directed or undirected) with positive edge weights and a source node s. •Postconditions: Finds a shortest weighted path from s to each node v and its length.
- 69. Dijkstra's Shortest-Weighted Paths s u v 100 1 1 1 1 w r Lengthof shortest path from s to u? 4
- 70. So far, thenodes have been found in order of length from s. BFS s u v 100 1 1 1 1 w r Which node is found first? Is the same true for Dijkstra's Alg?
- 71. So far, thenodes have been found in order of length from s. s u v 100 1 1 1 1 w r It has the longest path from s. Which node is found first? Is the same true for Dijkstra's Alg? BFS
- 72. So far, thenodes have been found in order of length from s. s u v 100 1 1 1 1 w r In what order do we handle the FoundNotHandled nodes? handled Dijkstra's Handle node that seems to be closest to s.
- 73. To prove pathis shortest: Prove there is a path of this length. Prove there are no shorter paths. Give a path (witness) Dijkstra's So far, the nodes have been handled in order of length from s. Post Conditions: Finds a shortest weighted path from s to each node v and its length.
- 74. To prove pathis shortest: Prove there is a path of this length. Prove there are no shorter paths. Dijkstra's When we handle v, we know there isn't a shorter path to it because ? Otherwise, we would have handled it already. Post Conditions: Finds a shortest weighted path from s to each node v and its length. So far, the nodes have been handled in order of length from s.
- 75. Basic Steps: u The shortestof handled paths to u has length d(u) Dijkstra's & there is an edge from u to v w<u,v> vs The shortest of handled paths to v has length d(v) The shortest known path to v has length min( d(v), d(u)+w<u,v> ). Handle node that seems to be closest to s. Need to keep approximate shortest distances.
- 76.
- 77. Dijkstra's The shortest ofhandled paths to v has length d(v) u vs
- 78. Dijkstra's u vs Handled nodes Foundnodes Handled Edges? The shortest of handled paths to v has length d(v)
- 79. Dijkstra's u vs Handled Nodes FoundNodes Handled Edges The shortest of handled paths to v has length d(v) Handled Paths?
- 80. Dijkstra's u vs Handled Nodes FoundNodes Handled Edges The shortest of handled paths to v has length d(v) Handled Paths
- 81. Dijkstra's u vs Handled Nodes The shortestof handled paths to v has length d(v) d(v) is the length of the shortest handled paths to v. For handled u, d(u) is the length of the shortest paths to u. NotFound d(v’)= ∞
- 82.
- 83. Dijkstra's For handled w, d(w)is the length of the shortest paths to w. Handle node with smallest d(u). For handled u, d(u) is the length of the shortest paths to u. d(v) is the length of the shortest handled path to v.
- 84. Dijkstra's For handled w, d(w)is the length of the shortest paths to w. Handle node with smallest d(u). For handled u, d(u) is the length of the shortest paths to u. d(u) is the length of the shortest handled path to u. d(u)
- 85. Dijkstra's For handled w, d(w)is the length of the shortest paths to w. Handle node with smallest d(u). For handled u, d(u) is the length of the shortest paths to u. d(u) d(u) is the length of the shortest handled path to u. First not handled node in path.
- 86. Dijkstra's For handled w, d(w)is the length of the shortest paths to w. Handle node with smallest d(u). For handled u, d(u) is the length of the shortest paths to u. d(u) First not handled node in path.d(u’) d(u) & d(u’) are the length of the shortest handled paths to u and u’.
- 87. Dijkstra's d(v) is thelength of the shortest handled path to v. For handled w, d(w) is the length of the shortest paths to w. Handle node with smallest d(u). d(v) is the length of the shortest handled path to v. d(u) d(v) w<u,v> d(v) = min( d(v), d(u)+w<u,v> ).
- 88. Time = O(E) Eachedge visited, times.2 ? Dijkstra's This number of times following an edge. Must update Priority Queue. Takes time O(log(n)) Time = O(E log(n)) For each update, d(v) = min( d(v), d(u)+w<u,v> ). Heap
- 89. Dijkstra's Shortest-Weighted Paths Specification:Dijkstra's Shortest-Weighted Paths Reachability-from-single-source s •Preconditions: The input is a graph G (either directed or undirected) with positive edge weights and a source node s. •Postconditions: Finds a shortest weighted path from s to each node v and its length. EndingInitial ConditionsMake Progress Maintain Loop InvDefine Exit ConditionDefine Step Define Measure of Progress Define Loop Invariants Define Problem km∞ 79 km to school Exit Exit 79 km 75 km Exit Exit 0 km Exit
- 90.
- 91.
- 92. Graph Search Handle somefoundNotHandled node •Queue: Handle in order found. •Breadth-First Search •Stack: Handle most recently found •Depth-First Search •Priority Queue: Handle node that seems to be closest to s. •Shortest (Weighted) Paths:
- 93.
- 94.
- 95.
- 96.
- 97.
- 98. DFS The nodes inthe stack form a path starting at s.
- 99.
- 100.
- 101.
- 102.
- 103.
- 104.
- 105.
- 106.
- 107.
- 108.
- 109.
- 110.
- 111.
- 112.
- 113.
- 114.
- 115. DFS s a c h k f i l m j e b g d s,1 Found Not Handled Stack <node,# edges> a,1 c,2 i,4 g,1 j,1 BackEdge to node on Stack Forms a cycle
- 116.
- 117.
- 118.
- 119.
- 120.
- 121.
- 122.
- 123.
- 124.
- 125.
- 126.
- 127.
- 128.
- 129.
- 130.
- 131.
- 132.
- 133.
- 134.
- 135.
- 136.
- 137.
- 138.
- 139.
- 140.
- 141.
- 144.
- 146. Ingredients: •Instances: The possibleinputs to the problem. •Solutions for Instance: Each instance has an exponentially large set of solutions. •Cost of Solution: Each solution has an easy to compute cost or value. Specification •Preconditions: The input is one instance. •Postconditions: An valid solution with optimal cost. (minimum or maximum) Optimization Problems
- 147. Specification: Network Flow •Preconditions: Theinput is a network G directed edges with capacities, a source node s, and a sink node t. •Postconditions: Finds a Maximum Flow F. Network Flow
- 148. Network Flow No leaks,not extra flow Value of flow = flow out of s = flow into t = flow across any cut
- 149.
- 150. Network Flow •Given FlowF •Construct Augmenting Graph GF •Find path P using BFS, DFS, or generic search algorithm •Let w be the max amount flow can increase along path P. •Increase flow along path P by w. i.e newF = oldF + w × P
- 151.
- 152. Hill Climbing We havea valid solution. (not necessarily optimal) Take a step that goes up. measure progress Value of our solution. Problems: Exit Cant take a step that goes up. Running time? Initially have the “zero” solution Local Max Global Max Can our Network Flow Algorithm get stuck in a local maximum? Make small local changes to your solution to construct a slightly better solution.
- 153. Network Flow Previous Input PreviousOutput Same Input Yes! Our Network Flow Algorithm can get stuck. Worse Output Need only one example.
- 154.
- 155.
- 156.
- 157.
- 158. Network Flow Previous Input PreviousOutput Same Input Yes! Our Network Flow Algorithm can get stuck. Worse Output Need only one example.
- 159. Hill Climbing Avoiding gettingstuck in a local maximum Good ExecutionBad Execution •Made better choices of direction •Hard •Back up an retry •Exponential time •Define a bigger step
- 160. Hill Climbing Different Solutions Current Solution Alg defines towhere alg can step i.e. what small local changes can be made to current solution This defines the topography
- 161. Hill Climbing Different Solutions Current Solution Define aslightly bigger step This defines the topography Perhaps removes some local maxima
- 162. Network Flow Previous Input PreviousOutput Same Input Yes! Our Network Flow Algorithm can get stuck. Worse Output Need only one example. Mistake? Putting 2 through this edge
- 163. Network Flow u v 0/75 0/10 FlowGraph u v 75 10 Augmentation Graph 75-21=54 21+10=31 u v 21/75 10 Flow Graph u v Augmentation Graph 2
- 164.
- 165.
- 166.
- 167.
- 168.
- 169.
- 171.
- 173.
- 176.
- 177. A Hotdog A combinationof pork,A combination of pork, grain, and sawdust, …grain, and sawdust, … Constraints:Constraints: •Amount of moistureAmount of moisture •Amount of protean,Amount of protean, •……
- 178. The Hotdog Problem Giventoday’s prices, what is a fast algorithm to find the cheapest hotdog?
- 179. There are deepideas within the simplicity. = AbstractionAbstraction Goal: Understand and think about complex things in simple ways. There are deep ideas within the simplicity. Rudich www.discretemath.com
- 180. Abstract Out EssentialDetails Cost: 29, 8, 1, 2 Amount to add: x1, x2, x3, x4 pork grain water sawdust 3x1 + 4x2 – 7x3 + 8x4 ≥ 12 2x1 - 8x2 + 4x3 - 3x4 ≥ 24 -8x1 + 2x2 – 3x3 - 9x4 ≥ 8 x1 + 2x2 + 9x3 - 3x4 ≥ 31 Constraints:Constraints: •moisturemoisture •protean,protean, •…… 29x1 + 8x2 + 1x3 + 2x4Cost of Hotdog:Cost of Hotdog:
- 181. 3x1 + 4x2– 7x3 + 8x4 ≥ 12 2x1 - 8x2 + 4x3 - 3x4 ≥ 24 -8x1 + 2x2 – 3x3 - 9x4 ≥ 8 x1 + 2x2 + 9x3 - 3x4 ≥ 31 29x1 + 8x2 + 1x3 + 2x4 Subject to:Subject to: Minimize:Minimize: Abstract Out Essential Details
- 182. A Fast Algorithm Fordecades people thought that there was no fast algorithm. Then one was found! Theoretical Computer Science finds new algorithms every day. 3x1 + 4x2 – 7x3 + 8x4 ≥ 12 2x1 - 8x2 + 4x3 - 3x4 ≥ 24 -8x1 + 2x2 – 3x3 - 9x4 ≥ 8 x1 + 2x2 + 9x3 - 3x4 ≥ 31 29x1 + 8x2 + 1x3 + 2x4 Subject to:Subject to: Minimize:Minimize: ≈
- 184.