The document describes several sorting algorithms including Radix Sort, Bucket Sort, Quick Sort, Merge Sort, and Counting Sort, detailing their methods and examples. Radix Sort organizes integers by significant digits, while Bucket Sort partitions data into buckets for partial sorting. Quick Sort is efficient with average complexity of O(n log n), and Merge Sort employs a divide and conquer strategy, whereas Counting Sort is focused on sorting small integers based on their keys.

1. Data Structure
Software Engineering

2. Radix sort
Radix sort is a non-comparative integer sorting
algorithm that sorts data with integer keys by
grouping keys by the individual digits which share
the same significant position and value.
Radix sort is one of the linear sorting algorithms for
integers.

3. Example
 The Original unsorted list
170, 045, 075, 090, 002, 024, 802, 066
 Sorting by least significant digit (1s place) gives:
170, 90, 802, 2, 24, 45, 75, 66
Notice that we keep 802 before 2, because 802 occurred before 2 in the original
and similarly for pairs 170 & 90 and 45 & 75.
 Sorting by next digit (10s place) gives:
802, 2, 24, 45, 66, 170, 75, 90
Notice that 802 again comes before 2 as 802 comes before 2 in the previous list.
 Sorting by most significant digit (100s place) gives:
2, 24, 45, 66, 75, 90, 170, 802

4. First counting
 The first counting pass starts on the least significant digit of
each key, producing an array of bucket sizes:
2 (bucket size for digits of 0: 170, 090)
2 (bucket size for digits of 2: 002, 802)
1 (bucket size for digits of 4: 024)
2 (bucket size for digits of 5: 045, 075)
1 (bucket size for digits of 6: 066)

5. Second counting
 A second counting pass on the next more significant digit of
each key will produce an array of bucket sizes:
2 (bucket size for digits of 0: 002, 802)
1 (bucket size for digits of 2: 024)
1 (bucket size for digits of 4: 045)
1 (bucket size for digits of 6: 066)
2 (bucket size for digits of 7: 170, 075)
1 (bucket size for digits of 9: 090)

6. Third and Final counting
 A third and final counting pass on the most significant digit of
each key will produce an array of bucket sizes:
6 (bucket size for digits of 0: 002, 024, 045, 066, 075, 090)
1 (bucket size for digits of 1: 170)
1 (bucket size for digits of 8: 802)

7. Alogrithm
 RADIX-SORT (A,d)
1. for I = 1 to d
2. use a stable sort to sort array A on digit i

8. Disadvantages
Still, there are some tradeoffs for Radix Sort that can
make it less preferable than other sorts.
The speed of Radix Sort largely depends on the inner
basic operations, and if the operations are not efficient
enough, Radix Sort can be slower than some other
algorithms such as Quick Sort and Merge Sort.
These operations include the insert and delete functions
of the sublists and the process of isolating the digit you
want.

9. Bucket sort
Bucket sort, or bin sort, is a sorting algorithm that
works by partitioning an array into a number
of buckets.
Bucket Sort is a sorting method that subdivides the
given data into various buckets depending on certain
characteristic order, thus partially sorting them in the
first go.

10. Example
 The Elements are distributed among bins

11.  The Then, elements are sorted within each bin

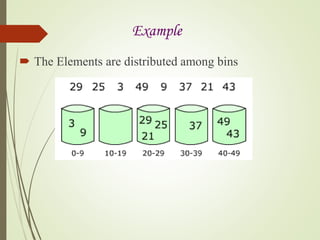
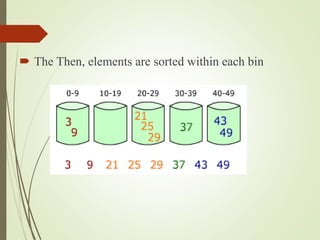
12. The Algorithm of Bucket-SORT
BUCKET SORT (A)
1. Let B[0..n – 1] be a new array
2. N = A.length
3. For I = 0 to n – 1
4. make B[i] an empty list
5. For I = 1 to n
6. insert A[i] into list B[[nA[i]]]
7. For I = 0 to n – 1
8. sort list B[i] with insertion sort
9. Concatenate the lists B[0], B[1],..B[n-1] together in order.

13. Quick sort
 Quick sort, or partition-exchange sort, is a sorting algorithm
developed by Tony Hoare that, on average, makes O(n log
n) comparisons to sort n items. Quick sort is a very efficient
sorting algorithm invented by C.A.R. Hoare.
 It has two phases:
• the partition phase and
• the sort phase

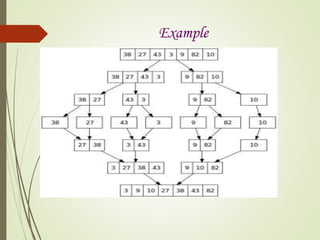
14. Example
 Short Example of a Quick sort Routine (Pivots chosen "randomly")
Input: [13 81 92 65 43 31 57 26 75 0]
Pivot: 65
Partition: [13 0 26 43 31 57] 65 [ 92 75 81]
Pivot: 31 81
Partition: [13 0 26] 31 [43 57] 65 [75] 81 [92]
Pivot: 13
Partition: [0] 13 [26] 31 [43 57] 65 [75] 81 [92]
Combine: [0 13 26] 31 [43 57] 65 [75 81 92]
Combine: [0 13 26 31 43 57] 65 [75 81 92]
Combine: [0 13 26 31 43 57 65 75 81 92]

15. Algorithm:
1. QUICKSORT(A, p, r)
2. if p < r
3. q = PARTITION(A, p, r)
4. QUICKSORT(A, p, q -1)
5. QUICKSORT(A, q +1, r)

16. Advantage
 One of the fastest algorithms on average.
 Does not need additional memory (the sorting takes place in
the array - this is called in-place processing). Compare with
merge sort: merge sort needs additional memory for
merging.

17. Merge sort
 Merge sort is an O(n log n) comparison-
based sorting algorithm.
 Most implementations produce a stable sort, meaning that
the implementation preserves the input order of equal
elements in the sorted output.
 It is a divide and conquer algorithm.
 Merge sort is based on the divide-and-conquer paradigm.

18. • Divide Step
If a given array A has zero or one element, simply return; it is
already sorted. Otherwise, split A[p .. r] into two
subarrays A[p .. q] and A[q + 1 .. r], each containing about half
of the elements of A[p .. r]. That is, q is the halfway point
of A[p .. r].

19. • Combine Step
Combine the elements back in A[p .. r] by merging the two sorted
subarrays A[p .. q] and A[q + 1 .. r] into a sorted sequence. To
accomplish this step, we will define a procedure MERGE
(A, p, q, r).
• Conquer Step
Conquer by recursively sorting the two subarrays A[p .. q]
and A[q + 1 .. r].

20. Example

21. Algorithm:
 MERGE-SORT (A, p, r)
IF p < r // Check for base case
THEN q = FLOOR[(p + r)/2] // Divide step
MERGE (A, p, q) // Conquer step.
MERGE (A, q + 1, r) // Conquer step.
MERGE (A, p, q, r) // Conquer step.

22. Counting sort
In computer science, counting sort is an algorithm
for sorting a collection of objects according to keys
that are small integers; that is, it is an
integer sorting algorithm

23. Example
 Input array {3, 4, 3, 2, 1}, the maximum entry is 4 and size is 5
Create a counting array {0, 0, 0, 0}, size is 4
Iterate over the input array, and add count to the appropriate index:
{3, 4, 3, 2, 1} -> {0, 0, 1, 0}
{3, 4, 3, 2, 1} -> {0, 0, 1, 1}
{3, 4, 3, 2, 1} -> {0, 0, 2, 1}
{3, 4, 3, 2, 1} -> {0, 1, 2, 1}
{3, 4, 3, 2, 1} -> {1, 1, 2, 1}
 The counting array is currently {1, 1, 2, 1}, we now can override the input
array to create our sorted list.
{0, 1, 2, 1} -> {1, 4, 3, 2, 1}
{o, o, 2, 1} -> {1, 2, 3, 2, 1}
{o, o, 1, 1} -> {1, 2, 3, 2, 1}
{o, o, o, 1} -> {1, 2, 3, 3, 1}
{o, o, o, o} -> {1, 2, 3, 3, 4}
 We are now done, the input (now output) array consists of {1, 2, 3, 3, 4} in
the proper order.

24. Algorithm
1. Counting-Sort (A,B,k)
2. For I = 0 to k
3. C[i] = 0
4. For j = 1 to A.length
5. C[A[j]] = C[A[j]] + 1
6. // C[i] now contains the number of elements equal to I
7. For I = 1 to k
8. C[i] = C[i] + C[I – 1]
9. // C[i] now contains the number of elements less than or equal to i.
10. For j = A.length downto 1
11. B[C[A[j]]] = A[j]
12. C[A[j]] = C[A[j]] – 1