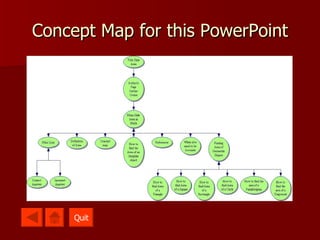
This interactive PowerPoint presentation defines area and explains how to calculate the area of different geometric shapes like triangles, squares, rectangles, circles, parallelograms, and trapezoids. It also discusses finding the area of irregular shapes and when accuracy is important in area measurements. The presentation was created by Justine Coxon, a mathematics education student, to help teach the concept of area.

1. Area of An Object Interactive PowerPoint Presentation By, Justine Coxon Created for ED 205-02 Quit

2. About the Author My name is Justine Coxon, and I am currently a student at Grand Valley State University, located in Allendale, Michigan. I am majoring in mathematics with an emphasis in Elementary Education. Some day I hope to become a teacher so that I can help students understand that mathematics can be fun! Email Her By Clicking the Address Below [email_address] Quit

3. Area What is Area Finding Area of a Geometric Shape Finding Area of an Irregular Shape When to be Accurate Mini Quiz References Used Concept Map Quit

4. What is Area The dictionary defines area as the quantitative measure of a plane or curved surface; two-dimensional extent. Personally, I would define area as, space that an object takes up, which can be measured by a unit. Quit

5. Finding the Area of Geometric Shapes Finding the Area of a Triangle Finding the Area of a Square Finding the Area of a Rectangle Finding the Area of a Circle Finding the Area of a Parallelogram Finding the Area of a Trapezoid Quit

6. Finding the Area of a Triangle We know that a triangle is a three sided figure whose interior angles add to be 180 °. To find the area of a triangle we need two measurements: the height (h in the diagram below) and the base (b in the diagram below). Once we have these measurements we plug them into this formula to find the total area of the triangle: Area of a Triangle = ½ b × h Quit Back to Geo-shapes

7. Finding the Area of a Square We know that a square is a shape that has four sides of equal length and has four 90 ° angles. To find the area of a square we need one measurement: the length of one side (a in the diagram below). Once we have this measurement we plug it into the formula below to find the area of a square: Area of a square = a 2 Note: a 2 is the same as a × a and we only need one measurement because all sides are equal Quit Back to Geo-shapes

8. Finding the Area of a Rectangle We know that a rectangle is a four sided figure, with two different sets of equal sides and interior angles each equal 90 °. To find the area of a rectangle we need two measurements: the length of one side (l in the diagram below) and the width of the other side (w in the diagram below); these should be different numbers. Once we have these measurements we plug them into this formula to find the total area of the rectangle: Area of a Rectangle = l × w Quit Quit Back to Geo-shapes

9. Finding the Area of a Circle We know that a circle is a round figure with not sides, but a continuous line around the outside . To find the area of a circle we need one measurement: the length of the radius (r in the diagram below). The radius is the line from the center of the circle to the outer edge of the circle and it will always be the same length no matter where we draw the end to at the outer edge. Once we have this measurement we plug it into the formula below to find the area of a circle: Area of a Circle = π × r 2 Quit Quit Back to Geo-shapes

10. Finding the Area of a Parallelogram We know that a parallelogram is a four sided figure, with two different sets of parallel sides figure and their interior angles add to be 360 °. To find the area of a parallelogram we need two measurements: the base (b in the diagram below) and the height (h in the diagram below). Once we have these measurements we plug them into this formula to find the total area of the parallelogram: Area of a Parallelogram = b × h Note: The equation is the same as the equation for a rectangle this is because if you were to cut one triangle from one side off and move it to the other side you would have a rectangle. Quit Quit Back to Geo-shapes

11. Finding the Area of a Trapezoid We know that a trapezoid is a shape that has four sides and one set of parallel lines . To find the area of a trapezoid we need three measurements: the base (b in the diagram below), the height (h in the diagram below), and the other parallel side to the base (a in the diagram below). Once we have this measurement we plug it into the formula below to find the area of a Trapezoid: Area of a Trapezoid = ½ × (a + b) × h Quit Quit Back to Geo-shapes

12. Finding the Area of an Irregular Shape An irregular shape is a shape that does not fit into the classification of a geometric shape and the area will be an estimation. These are the steps to finding the area of an irregular shape: Draw a picture of the irregular shape to scale Create a grid over the irregular shape, in most cases the grid consists of squares Count the whole grid units that cover the irregular object Estimate the size of the non-whole units Add all the units whole and non-whole to get close to the total area of the irregular object Below is a link to a short video that discusses finding the area of a section of the Grand Canyon, you can also find more information by visiting Dr. Math at: http://mathforum.org/library/drmath/sets/select/dm_area_irreg.html Quit Click Here to Watch Video

13. When to be Accurate There some cases where you need to be extremely accurate in your measurements. This cases usually include measuring small objects and when the measurement is important, for example: When you are measuring the space for your new cupboards When you are measuring how many square millimeters are in two square inches When measuring the amount of carpet you need for a room In other cases where the measurement isn’t as important or you are measuring a larger object you do not need to be as accurate, for example: When measuring how many square feet are in a football field When measuring the amount of space that land takes up, as opposed to water, on Earth When measuring the space one parking spot takes up in the parking lot Below is a link to a video which includes examples of when measurements need to be accurate Quit Click Here to Watch Video

14. Mini Quiz The definition of area is length multiplied by the width. Agree Disagree Sometimes when you find the area of something you do not have to be actually accurate. Agree Disagree To find the Area of a Square you solve a 2 which is the same thing as a × a. Agree Disagree When finding the area of a circle you solve π r 2 where r is the diameter of the circle. Agree Disagree Quit

15. References Used http://www.mathsisfun.com/area.html Math Monsters: Area, Discovering Math: Measurement, Discovering Math: Concepts in Geometry, Mica with ruler, Grand Canyon, Teacher, Cat at Desk, and Balloons http://streaming.discoveryeducation.com/ http://math.about.com/od/formulas/ss/areaperimeter_4.htm http://math.about.com/od/formulas/ss/areaperimeter_3.htm http://math.about.com/od/formulas/ss/areaperimeter_2.htm http://math.about.com/od/formulas/ss/areaperimeter.htm Quit

16. Concept Map for this PowerPoint Quit

17. Please Try Again Quit Return to Mini Quiz

18. You Answered Correctly Quit Return to Mini Quiz

19. Quit Return to Previous Click the picture above to start video

20. Click the picture above to start video Quit Return to Previous