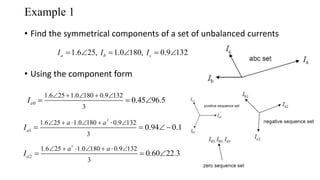
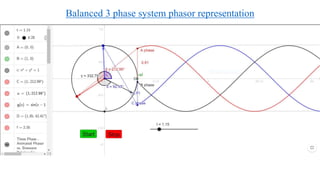
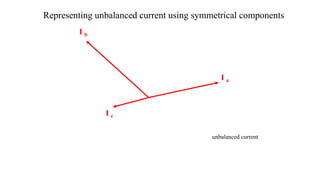
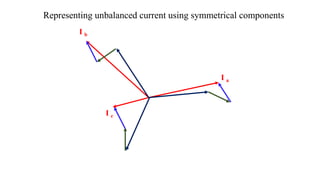
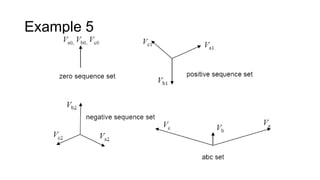
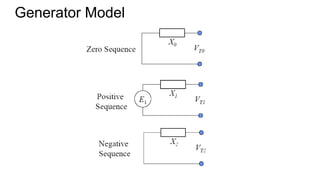
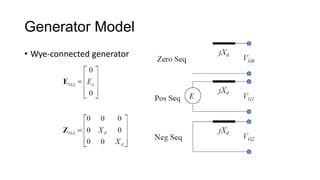
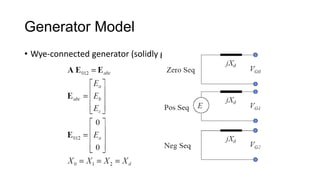
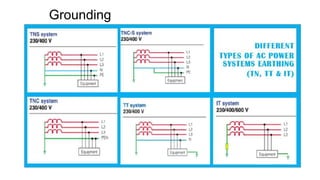
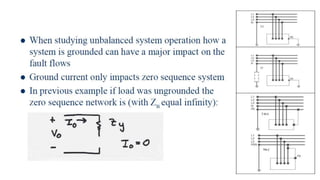
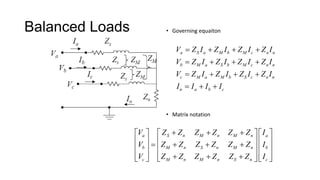
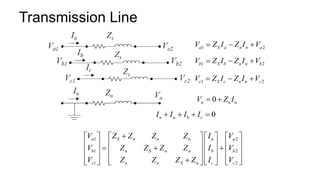
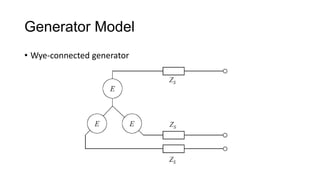
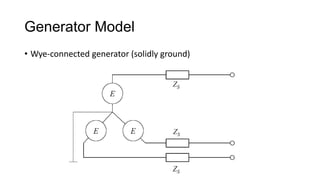
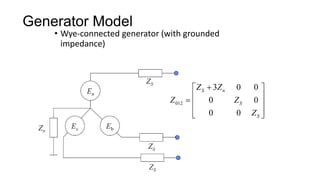
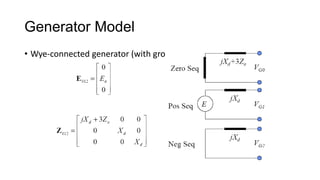
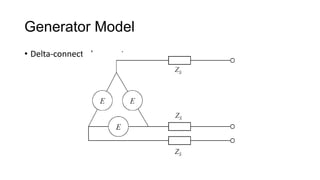
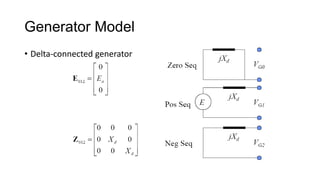
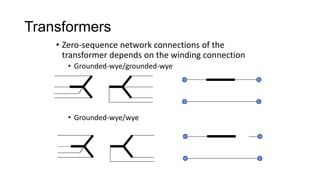
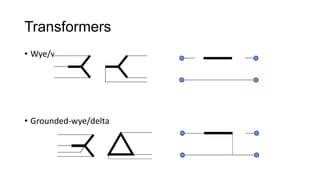
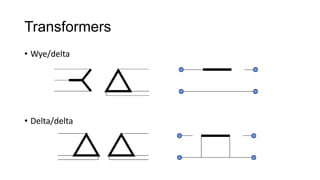
1. The document discusses symmetrical components, which allow representation of unbalanced three-phase quantities as the sum of three balanced components. 2. It introduces the positive, negative, and zero sequence components and the transformation matrix used to relate the symmetrical components to the original unbalanced quantities. 3. Symmetrical components are useful for simplifying analysis of unbalanced conditions like single line-to-ground faults in power systems. Sequence impedances can be used to model devices and transmission lines.

1. 1
POWER SYSTEMS
SUBJECT NAME : POWER SYSTEMS
CHAPTER NO: 1
CHAPTER NAME : POWER SYSTEM
FUNDAMENTALS
(Basic Concepts )
LECTURE : 3

2. 1. Basic Concepts
2. Synchronous Machines and
Transformer Modelling
3. Transmission Line Modelling
4. Power Flow Analysis
5. Fault Analysis
6. Power System Stability
7. Economic Operation of Power
System,
Power System Class Arrangement
Chapters

3. Symmetrical Components

4. Balanced 3 phase system phasor representation

6. I a
I b
I c
Representing unbalanced current using symmetrical components
unbalanced current

7. I a
I b
I c
Representing unbalanced current using symmetrical components

8. Representing unbalanced current using symmetrical components

9. Representing unbalanced current using symmetrical components

10. Representing unbalanced current using symmetrical components

11. Representing unbalanced current using symmetrical components

12. Representing unbalanced current using symmetrical components

13. Representing unbalanced current using symmetrical components

14. Representing unbalanced current using symmetrical components

15. Representing unbalanced current using symmetrical components

16. I a
I b
I c
Representing unbalanced current using symmetrical components
More Examples

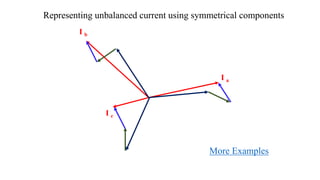
18. In 1918 Charles Legeyt Fortescue presented a paper[3] which demonstrated that
any set of N unbalanced phasors (that is, any such polyphase signal) could be
expressed as the sum of N symmetrical sets of balanced phasors, for values of N
that are prime. Only a single frequency component is represented by the phasors.
In 1943 Edith Clarke published a textbook giving a method of use of
symmetrical components for three-phase systems that greatly simplified
calculations over the original Fortescue paper.[4] In a three-phase system, one set
of phasors has the same phase sequence as the system under study (positive
sequence; say ABC), the second set has the reverse phase sequence (negative
sequence; ACB), and in the third set the phasors A, B and C are in phase with
each other (zero sequence, the common-mode signal). Essentially, this method
converts three unbalanced phases into three independent sources, which
makes asymmetric fault analysis more tractable.

19. Edith Clarke (February 10, 1883 – October 29,
1959) was the first woman to be professionally
employed as an electrical engineer in the United
States,[1] and the first female professor of
electrical engineering in the country.[2] She was
the first woman to deliver a paper at
the American Institute of Electrical Engineers,
the first female engineer whose professional
standing was recognized by Tau Beta Pi, and the
first woman named as a Fellow of the American
Institute of Electrical Engineers. She specialized
in electrical power system analysis[3] and
wrote Circuit Analysis of A-C Power Systems.[4]

20. By expanding a one-line diagram to show the positive sequence, negative
sequence, and zero sequence impedances of generators, transformers and other
devices including overhead lines and cables, analysis of such unbalanced
conditions as a single line to ground short-circuit fault is greatly simplified. The
technique can also be extended to higher order phase systems.
Physically, in a three phase system, a positive sequence set of currents produces a
normal rotating field, a negative sequence set produces a field with the opposite
rotation, and the zero sequence set produces a field that oscillates but does not
rotate between phase windings. Since these effects can be detected physically
with sequence filters, the mathematical tool became the basis for the design
of protective relays, which used negative-sequence voltages and currents as a
reliable indicator of fault conditions. Such relays may be used to trip circuit
breakers or take other steps to protect electrical systems.
The analytical technique was adopted and advanced by engineers at General
Electric and Westinghouse, and after World War II it became an accepted method
for asymmetric fault analysis.

21. Symmetrical Components
• Unbalanced three-phase quantities may be replaced by the sum of
three separate but balanced symmetrical components
• applicable to current and voltages

22. • Positive sequence phasors
2
1 1 1 1
( 240) ( 120)
b a a a
I I I a I
 
      
1 1 1
a a a
I I I

  
1 1 1 1
( 120) ( 240)
c a a a
I I I aI
 
      

23. • Negative sequence phasors
2 2 2
a a a
I I I

  
2 2 2 2
( 120) ( 240)
b a a a
I I I aI
 
      
2
2 2 2 2
( 240) ( 120)
c a a a
I I I a I
 
      

24. • Zero sequence phasors
0 0 0
a a a
I I I

  
0 0 0
b a a
I I I

  
0 0 0
c a a
I I I

  

25. • Operator “a” and its identities
1 120 1 240 0.5 0.866
a j
      
2
1 240 1 120 0.5 0.866
a j
      
3
1 0 1 0
a j
   
2
1 0
a a
  

27. • Relating unbalanced phasors to symmetrical
components
0 1 2
a a a a
I I I I
  
2
0 1 2 0 1 2
b b b b a a a
I I I I I a I aI
     
2
0 1 2 0 1 2
c c c c a a a
I I I I I aI a I
     
0
2
1
2
2
1 1 1
1
1
a a
b a
c a
I I
I a a I
I a a I
     
     

     
     
     

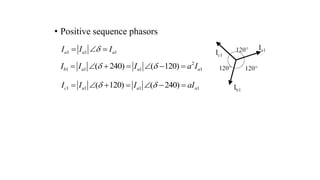
28. • In matrix notation
• or
• [A] is the symmetrical components transformation
matrix
0
2
1
2
2
1 1 1
1
1
a a
b a
c a
I I
I a a I
I a a I
     
     

     
     
     
2
2
1 1 1
1
1
a a
a a
 
 
  
 
 
A
abc 012
I = A I where

29. • Unbalanced three-phase quantities may be replaced by the sum of
three separate but balanced symmetrical components
• applicable to current and voltages
• Operator “a” and its identities
1 120 1 240 0.5 0.866
a j
      
2
1 240 1 120 0.5 0.866
a j
      
3
1 0 1 0
a j
   
2
1 0
a a
  

30. • Solving for the symmetrical components leads to
• In component form
1
012 abc


I A I where 1 2
2
1 1 1
1 1
1
3 3
1
a a
a a
 
 
 
 
 
 
 
A A
0
2
1
2
2
1
3
1
3
1
3
( )
( )
( )
a a b c
a a b c
a a b c
I I I I
I I aI a I
I I a I aI
  
  
  

31. • Similar expressions exist for voltages
• The apparent power of symmetrical components
012
abc 
V A V
1
012 abc


V A V
*
3
T
abc abc
S 
  V I T *
012 012
( ) ( )
 AV AI
T T * *
012 012
 V A A I
T *
012 012
3
 V I
* * *
0 0 1 1 2 2
3 3 3
a a a a a a
V I V I V I
  

32. • Find the symmetrical components of a set of unbalanced currents
• Using the component form
1.6 25, 1.0 180, 0.9 132
a b c
I I I
     
0
1.6 25 1.0 180 0.9 132
3
0.45 96.5
a
I
    
  
2
1
1.6 25 1.0 180 0.9 132
3
0.94 0.1
a
a a
I
     

  
2
2
1.6 25 1.0 180 0.9 132
3
0.60 22.3
a
a a
I
     

  
Example 1

33. Example 2

34. Example 3

35. Example 4

36. Example 4

37. Example 5
• Given a set of symmetrical components
• The abc components
0 1 2
0.6 90, 1.0 30, 0.8 30
a a a
V V V
     
0.6 90 1.0 30 0.8 30 1.7088 24.2
a
V        
2
0.6 90 (1.0 30) (0.8 30) 0.4 90
b
V a a
        
2
0.6 90 (1.0 30) (0.8 30) 1.7088 155.8
b
V a a
        

38. Example 5

39. Example 6

40. Use of Symmetrical Components

41. Use of Symmetrical Components

42. Networks are Now Decoupled

43. Grounding

47. Grounding, cont’d

48. Sequence Impedances
• The impedance in the flow of a sequence current creating sequence
voltages
• positive, negative, and zero sequence impedances
• Augmented network models
• wye-connected balanced loads
• transmission line
• 3-phase transformers
• generators

49. Balanced Loads • Governing equaiton
• Matrix notation
a S a M b M c n n
b M a S b M c n n
c M a M b S c n n
n a b c
V Z I Z I Z I Z I
V Z I Z I Z I Z I
V Z I Z I Z I Z I
I I I I
   
   
   
  
a S n M n M n a
b M n S n M n b
c M n M n S n c
V Z Z Z Z Z Z I
V Z Z Z Z Z Z I
V Z Z Z Z Z Z I
  
     
     
   
     
     
  
     

50. Balanced Loads
• Sequence impedance
abc abc abc

V Z I    
012 012
abc

A V Z A I
1
012 012
012
abc

 
  
Z
V A Z A I
1
012 abc

 
  
Z A Z A
2 2
2 2
1 1 1 1 1 1
1
1 1
3
1 1
S n M n M n
M n S n M n
M n M n S n
Z Z Z Z Z Z
a a Z Z Z Z Z Z a a
a a Z Z Z Z Z Z a a
  
     
     
   
     
     
  
     
3 2 0 0
0 0
0 0
S n M
S M
S M
Z Z Z
Z Z
Z Z
 
 
 
 
 
 

 

51. Transmission Line
0
n a b c
I I I I
   
1 2
a S a n n a
V Z I Z I V
  
1 2
b S b n n b
V Z I Z I V
  
1 2
c S c n n c
V Z I Z I V
  
0
n n n
V Z I
 
1 2
1 2
1 2
a S n n n a a
b n S n n b b
c n n S n c c
V Z Z Z Z I V
V Z Z Z Z I V
V Z Z Z Z I V

       
       
  
       
       

       

52. Transmission Line
• Sequence impedance
1 2
abc abc abc abc
 
V Z I V 012,1 012 012,2
abc
 
A V Z A I A V
1
012,1 012 012,2
012
abc

 
 
 
Z
V A Z A I V
1
012 abc

 
  
Z A Z A
2 2
2 2
1 1 1 1 1 1
1
1 1
3
1 1
S n n n
n S n n
n n S n
Z Z Z Z
a a Z Z Z Z a a
a a Z Z Z Z a a

     
     
 
     
     

     
3 0 0
0 0
0 0
S n
S
S
Z Z
Z
Z

 
 
  
 
 

53. Generators
• Similar to sequence impedances
• Typical values for generators
• the transient fault impedance is a function of time
• positive sequence values are the same for Xd, X’d, and Xd”
• negative sequence values are affected by the rotation of
the rotor (X2 ~ Xd”)
• zero sequence values are isolated from the airgap of the
machine
• the zero sequence reactance is approximated to the
leakage reactance (X0 ~ XL)

54. Generator Model

55. Generator Model
• Wye-connected generator

56. Generator Model
• Wye-connected generator

57. Generator Model
• Wye-connected generator (solidly ground)

58. Generator Model
• Wye-connected generator (solidly ground)

59. Generator Model
• Wye-connected generator (with grounded
impedance)
012
3 0 0
0 0
0 0
S n
S
S
Z Z
Z Z
Z

 
 
  
 
 

60. Generator Model
• Wye-connected generator (with grounded impedance)

61. Generator Model
• Delta-connected generator

62. 62
POWER SYSTEMS
SUBJECT NAME : POWER SYSTEMS
CHAPTER NO: 1
CHAPTER NAME : POWER SYSTEM
FUNDAMENTALS
(Basic Concepts )
LECTURE : 4

63. Generator Model
• Delta-connected generator

64. Transformers
• Series Leakage Impedance
• the magnetization current and core losses are neglected
(only 1% of the total load current)
• the transformer is modeled with the equivalent series
leakage impedance
• Three single-phase units
• the series leakage impedance is the same for all the
sequences
• Three-phase units
• the series leakage impedance is the same for the positive
and negative sequence
 
0 1 2 l
Z Z Z Z
  
 
1 2 l
Z Z Z
 

65. Transformers
• Wye-delta transformers phase shifting pattern
• The positive sequence quantities rotate by +30 degrees
• The negative sequence quantities rotate by -30 degrees
• The zero sequence quantities can not pass through the
transformer
• U.S. standard
• Independent of the winding order ( or )
• The positive sequence line voltage on the HV side leads the
corresponding line voltage on the LV side by 30 degrees
• For the negative sequence voltages the corresponding phase
shift is -30 degrees
Y
 Y

66. Transformers
• Zero-sequence network connections of the
transformer depends on the winding connection
• Grounded-wye/grounded-wye
• Grounded-wye/wye

67. Transformers
• Wye/wye
• Grounded-wye/delta

68. Transformers
• Wye/delta
• Delta/delta

69. Transformer Sequence Diagrams

70. Sequence Networks
• The zero-, positive-, and negative-sequence networks of system components—generators, motors,
transformers, and transmission can be used to construct system zero-, positive-, and negative-
sequence networks. We make the following assumptions:
• The power system operates under balanced steady-state conditions before the fault occurs. Thus
the zero-, positive-, and negative sequence networks are uncoupled before the fault occurs.
During unsymmetrical faults they are interconnected only at the fault location.
• Prefault load current is neglected. Because of this, the positive sequence internal voltages of all
machines are equal to the prefault voltage VF. Therefore, the prefault voltage at each bus in the
positive-sequence network equals VF.
• Transformer winding resistances and shunt admittances are neglected.
• Transmission-line series resistances and shunt admittances are neglected.
• Synchronous machine armature resistance, saliency, and saturation
• are neglected.
• Induction motors are either neglected (especially for motors rated 50 hp or less) or represented
in the same manner as synchronous machines.

71. Example 5

72. Example 5