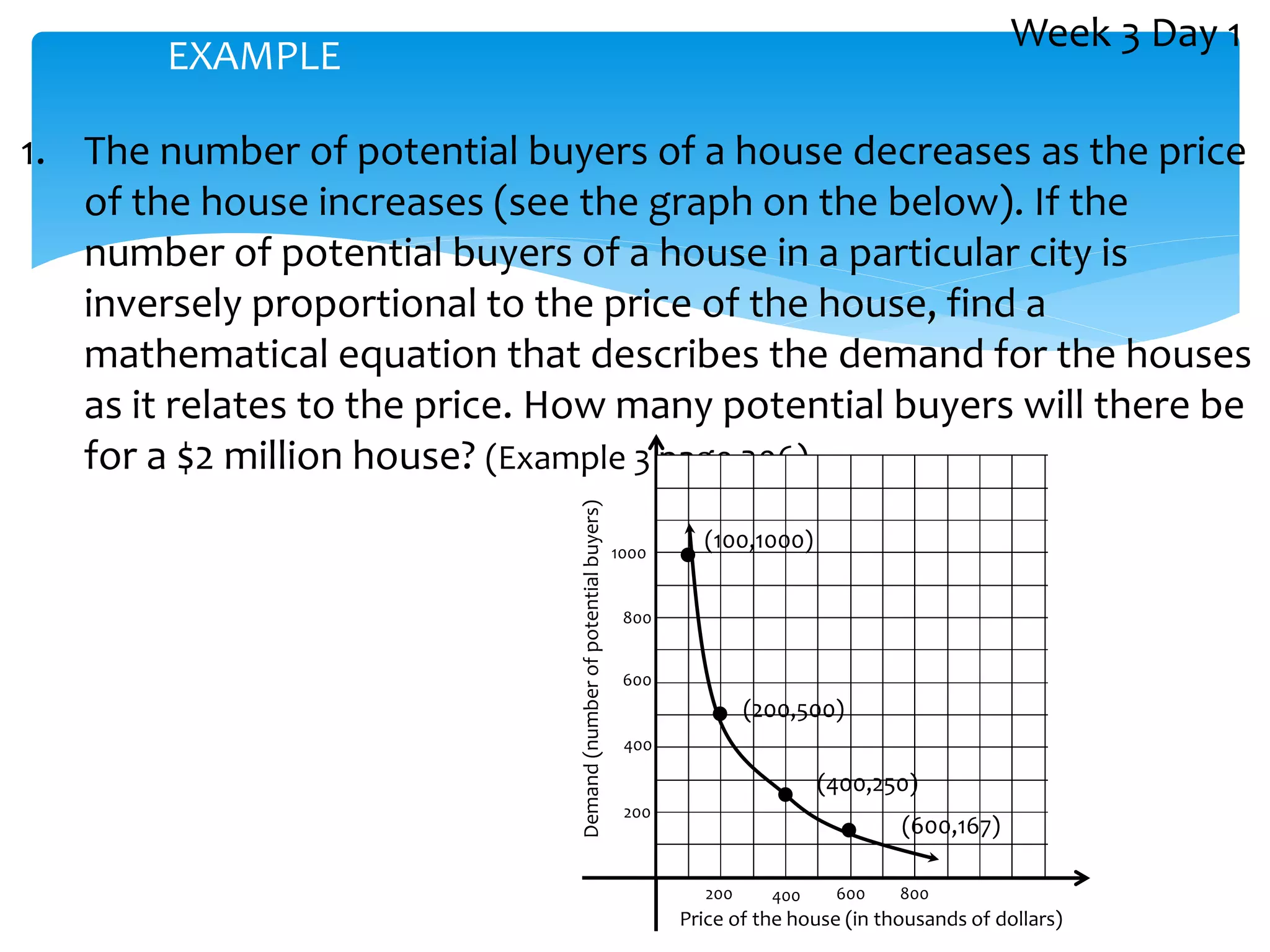
This document discusses ratios, proportions, and different types of variation. It defines ratio, proportion, and direct, inverse, joint, and combined variation. It provides examples of writing equations to describe each type of variation relationship between quantities. The objectives are for students to understand these concepts and be able to identify the different types of variation, understand the difference between direct and inverse variation, and develop mathematical models using different variations.

1. RATIO, VARIATION AND
PROPORTION
Prepared By:
Malik Sabah-ud-din
http://basic2advanced.blogspot.com
Web Site:

2.  Use ratio and proportion in solving problems involving them,
 Identify the different types of variation,
 Understand the difference between direct variation and
inverse variation,
 Understand the difference between combined variation and
joint variation, and
 Develop mathematical models using direct variation, inverse
variation, combined variation and joint variation.
TODAY’S OBJECTIVE
At the end of the lesson the students are expected
to:
Week 3 Day 1

3. Definition
RATIO
A ratio is an indicated quotient of two quantities. Every ratio is
a fraction and all ratios can be described by means of a
fraction. The ratio of x and y is written as x : y, it can also be
represented as
Thus,
y
x
y
x
y
:
x 
Week 3 Day 1

4. 1. Express the following ratios as simplified fractions:
a) 5 : 20
b) )
8
x
2
x
(
:
)
4
x
4
x
( 2
2




2. Write the following comparisons as ratios reduced to lowest
terms. Use common units whenever possible.
a) 4 students to 8 students
b) 4 days to 3 weeks
c) 5 feet to 2 yards
d) About 10 out of 40 students took Math Plus
EXAMPLE
Week 3 Day 1

5. Definition
PROPORTION
A proportion is a statement indicating the equality of two ratios.
Thus, , , are proportions.
In the proportion x : y = m : n, x and n are called the extremes, y
and m are called the means. x and m are the called the
antecedents, y and n are called the consequents.
In the event that the means are equal, they are called the mean
proportional.
n
m
y
x
 n
:
m
y
x
 n
:
m
y
:
x 
Week 3 Day 1

6. 1. Find the mean proportional of
2. Determine the value of x in the following proportion:
a) 2 : 5 = x : 20
b)
.
25
:
:
225 x
x 
4
1
x
20
x


EXAMPLE
Week 3 Day 1

7. Definition
VARIATION
A variation is the name given to the study of the effects of changes
among related quantities.
Variation describes the relationship between variables.
Week 3 Day 1

8. Direct Variation
When one quantity is a constant multiple of another quantity, we say
that the quantities are directly proportional to one another .
Let x and y represent two quantities. The following are equivalent
statements:
• y = kx, where k is a nonzero constant.
• y varies directly with x.
• y is directly proportional to x.
The constant k is called the constant of variation or the constant of
proportionality.
Definition page 304
Week 3 Day 1

9. Write an equation that describes each variation.
17. d is directly proportional to t. d=r when t=1.
19. V is directly proportional to both l and w. V=6h when w=3 qnd
h=4.
24. W is directly proportional to both R and the square of I. W=4
when R=100 and I=0.25.
(Exercises page 309)
EXAMPLE
Week 3 Day 1

10. 1. In the United States, the costs of electricity is directly
proportional to the number of kilowatt hours (kWh) used. If a
household in Tennessee on average used 3098 kWh per month
and had an average monthly electric bill of $179.99, find a
mathematical model that gives the cost of electricity in
Tennessee in terms of the number of kWh used. (Example 1 page
304)
2. Hooke’s Law states that the force needed to keep a spring
stretched x units beyond its natural length is directly proportional
x. Here the constant of proportionality is called a spring constant.
a) Write Hooke’s Law as an equation.
b) If a spring has a natural length of 10 cm and a force of 40 N is
required to maintain the spring stretched to a length of 15 cm,
find the spring constant.
c) What force is needed to keep the spring stretched to a length
of 14cm? ( Exercise 23 page 191 from Algebra & Trig. by Stewart, Redlin &
Watson, 2nd edition)
EXAMPLE
Week 3 Day 1

11. Direct Variation with Powers
Let x and y represent two quantities. The following are equivalent
statements:
• , where k is a nonzero constant.
• y varies directly with the nth power of x.
• y is directly proportional to the nth power of x.
Definition page 305
n
kx
y 
Week 3 Day 1

12. 1. A brother and sister have weight (pounds) that varies as the cube
of the cube of height (feet) and they share the same
proportionality constant . The sister is 6 feet tall and weighs 170
pounds. Her brother is 6’4” tall. How much does he weigh?
(Your Turn page 306)
EXAMPLE
Week 3 Day 1

13. Inverse Variation
Let x and y represent two quantities. The following are equivalent
statements:
• , where k is a nonzero constant.
• y varies inversely with x.
• y is inversely proportional to x.
The constant k is called the constant of variation or the constant of
proportionality.
Definition page 306
x
k
y 
Week 3 Day 1

14. 1. The number of potential buyers of a house decreases as the price
of the house increases (see the graph on the below). If the
number of potential buyers of a house in a particular city is
inversely proportional to the price of the house, find a
mathematical equation that describes the demand for the houses
as it relates to the price. How many potential buyers will there be
for a $2 million house? (Example 3 page 306)
EXAMPLE
200 400 600 800
200
600
400
800
1000 



(100,1000)
(200,500)
(400,250)
(600,167)
Price of the house (in thousands of dollars)
Demand
(number
of
potential
buyers)
Week 3 Day 1

15. Inverse Variation with Powers
Definition page 307
x.
of
power
nth
the
to
al
proportion
inversely
is
y
or
x,
of
power
nth
the
with
inversely
varies
y
that
say
we
then
,
x
k
y
equation
the
by
related
are
y
and
x
If n

Week 3 Day 1

16. Joint Variation and Combined Variation
• When one quantity is proportional to the product of two or more
other quantities, the variation is called joint variation.
Example: Simple interest which is defined as
• When direct variation and inverse variation occur at the same time,
the variation is called combined variation.
Example: Combined gas law in chemistry,
Definition page 307
V
T
k
P 
t
Pr
I
Week 3 Day 1

17. 1. The gas in the headspace of a soda bottle has a volume of 9.0 ml,
pressure of 2 atm (atmospheres), and a temperature of 298K
(standard room temperature of 77⁰F). If the soda bottle is stored
in a refrigerator, the temperature drops to approximately 279K
(42⁰F). What is the pressure of the gas in the headspace once the
bottle is chilled?
(Example 4 page 308)
EXAMPLE
Week 3 Day 1

18. Direct, inverse, joint and combined variation can be used to
model the relationship between two quantities. For two
quantities x and y we say that:


Joint variation occurs when one quantity is directly
proportional to two or more quantities.
Combined variation occurs when one quantity is directly
proportional to one or more quantities and inversely
proportional to one or more other quantities.
SUMMARY
kx.
y
if
x
to
al
proportion
directly
is
y 
.
x
k
y
if
x
to
al
proportion
inversely
is
y 
Week 3 Day 1