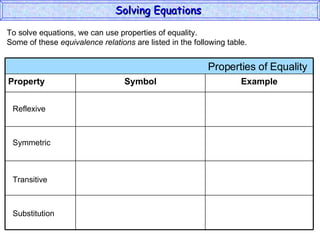
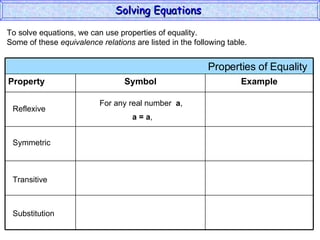
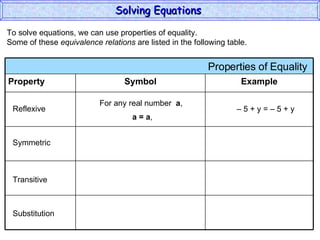
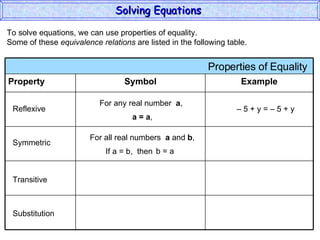
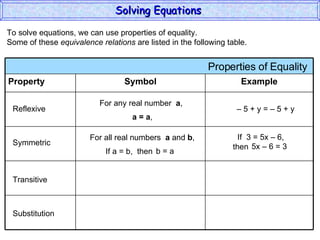
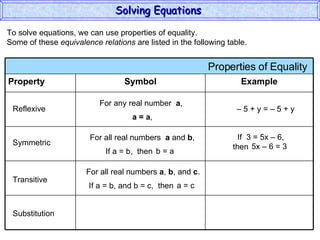
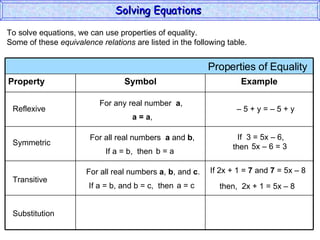
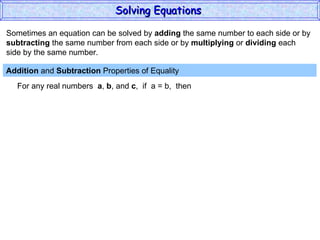
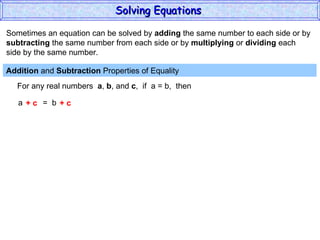
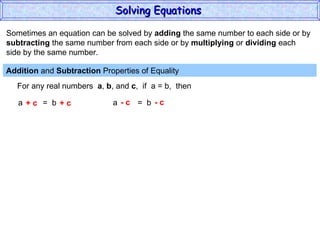
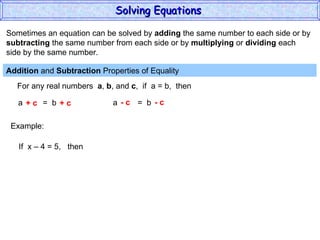
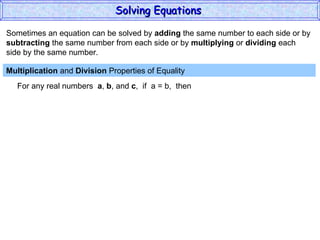
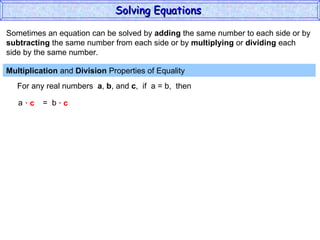
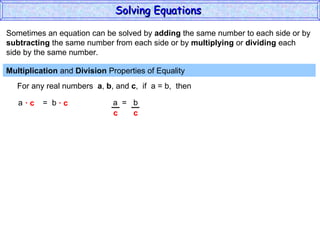
The document discusses solving equations. It defines key terms like open sentence and equation. It explains that an open sentence with variables is neither true nor false until the variables are replaced with numbers, with each valid replacement called a solution. It outlines properties of equality like reflexive, symmetric, and transitive properties that can be used to solve equations, such as adding or subtracting the same number to both sides.

1. Solving Equations

2. You'll Learn To: Solving Equations Vocabulary 1) open sentence 2) equation 3) solution Translate verbal expressions into algebraic expression and equations and vice versa. Solve equations using the properties of equality.

3. A mathematical sentence (expression) containing one or more variables is called an open sentence . Solving Equations

4. A mathematical sentence (expression) containing one or more variables is called an open sentence . A mathematical sentence stating that two mathematical expressions are equal is called an _________. Solving Equations

5. A mathematical sentence (expression) containing one or more variables is called an open sentence . A mathematical sentence stating that two mathematical expressions are equal is called an _________. equation Solving Equations

6. A mathematical sentence (expression) containing one or more variables is called an open sentence . A mathematical sentence stating that two mathematical expressions are equal is called an _________. equation Open sentences are neither true nor false until the variables have been replaced by numbers. Solving Equations

7. A mathematical sentence (expression) containing one or more variables is called an open sentence . A mathematical sentence stating that two mathematical expressions are equal is called an _________. equation Open sentences are neither true nor false until the variables have been replaced by numbers. Each replacement that results in a true statement is called a ________ of the open sentence. Solving Equations

8. Solving Equations A mathematical sentence (expression) containing one or more variables is called an open sentence . A mathematical sentence stating that two mathematical expressions are equal is called an _________. equation Open sentences are neither true nor false until the variables have been replaced by numbers. Each replacement that results in a true statement is called a ________ of the open sentence. solution

9. To solve equations, we can use properties of equality. Some of these equivalence relations are listed in the following table. Solving Equations

10. To solve equations, we can use properties of equality. Some of these equivalence relations are listed in the following table. Reflexive Symmetric Transitive Substitution Solving Equations Properties of Equality Property Symbol Example

11. To solve equations, we can use properties of equality. Some of these equivalence relations are listed in the following table. Reflexive Symmetric Transitive Substitution For any real number a , a = a , Solving Equations Properties of Equality Property Symbol Example

12. To solve equations, we can use properties of equality. Some of these equivalence relations are listed in the following table. Reflexive Symmetric Transitive Substitution For any real number a , a = a , – 5 + y = – 5 + y Solving Equations Properties of Equality Property Symbol Example

13. To solve equations, we can use properties of equality. Some of these equivalence relations are listed in the following table. Reflexive Symmetric Transitive Substitution For any real number a , a = a , For all real numbers a and b , If a = b, then b = a – 5 + y = – 5 + y Solving Equations Properties of Equality Property Symbol Example

14. To solve equations, we can use properties of equality. Some of these equivalence relations are listed in the following table. Reflexive Symmetric Transitive Substitution For any real number a , a = a , For all real numbers a and b , If a = b, then b = a – 5 + y = – 5 + y If 3 = 5x – 6, then 5x – 6 = 3 Solving Equations Properties of Equality Property Symbol Example

15. To solve equations, we can use properties of equality. Some of these equivalence relations are listed in the following table. Reflexive Symmetric Transitive Substitution For any real number a , a = a , For all real numbers a and b , If a = b, then For all real numbers a , b , and c . If a = b, and b = c, then b = a a = c – 5 + y = – 5 + y If 3 = 5x – 6, then 5x – 6 = 3 Solving Equations Properties of Equality Property Symbol Example

16. To solve equations, we can use properties of equality. Some of these equivalence relations are listed in the following table. Reflexive Symmetric Transitive Substitution For any real number a , a = a , For all real numbers a and b , If a = b, then For all real numbers a , b , and c . If a = b, and b = c, then b = a a = c – 5 + y = – 5 + y If 3 = 5x – 6, then 5x – 6 = 3 If 2x + 1 = 7 and 7 = 5x – 8 then, 2x + 1 = 5x – 8 Solving Equations Properties of Equality Property Symbol Example

17. To solve equations, we can use properties of equality. Some of these equivalence relations are listed in the following table. Reflexive Symmetric Transitive Substitution For any real number a , a = a , For all real numbers a and b , If a = b, then For all real numbers a , b , and c . If a = b, and b = c, then If a = b, then a may be replaced by b and b may be replaced by a. b = a a = c – 5 + y = – 5 + y If 3 = 5x – 6, then 5x – 6 = 3 If 2x + 1 = 7 and 7 = 5x – 8 then, 2x + 1 = 5x – 8 Solving Equations Properties of Equality Property Symbol Example

18. To solve equations, we can use properties of equality. Some of these equivalence relations are listed in the following table. Reflexive Symmetric Transitive Substitution For any real number a , a = a , For all real numbers a and b , If a = b, then For all real numbers a , b , and c . If a = b, and b = c, then If a = b, then a may be replaced by b and b may be replaced by a. b = a a = c – 5 + y = – 5 + y If 3 = 5x – 6, then 5x – 6 = 3 If 2x + 1 = 7 and 7 = 5x – 8 then, 2x + 1 = 5x – 8 If (4 + 5) m = 18 then 9m = 18 Solving Equations Properties of Equality Property Symbol Example

19. Sometimes an equation can be solved by adding the same number to each side or by subtracting the same number from each side or by multiplying or dividing each side by the same number. Solving Equations

20. Sometimes an equation can be solved by adding the same number to each side or by subtracting the same number from each side or by multiplying or dividing each side by the same number. Addition and Subtraction Properties of Equality For any real numbers a , b , and c , if a = b, then Solving Equations

21. Sometimes an equation can be solved by adding the same number to each side or by subtracting the same number from each side or by multiplying or dividing each side by the same number. Addition and Subtraction Properties of Equality For any real numbers a , b , and c , if a = b, then a = b + c + c Solving Equations

22. Sometimes an equation can be solved by adding the same number to each side or by subtracting the same number from each side or by multiplying or dividing each side by the same number. Addition and Subtraction Properties of Equality For any real numbers a , b , and c , if a = b, then a = b + c + c a = b - c - c Solving Equations

23. Sometimes an equation can be solved by adding the same number to each side or by subtracting the same number from each side or by multiplying or dividing each side by the same number. Addition and Subtraction Properties of Equality For any real numbers a , b , and c , if a = b, then a = b + c + c a = b - c - c Example: If x – 4 = 5, then Solving Equations

24. Sometimes an equation can be solved by adding the same number to each side or by subtracting the same number from each side or by multiplying or dividing each side by the same number. Addition and Subtraction Properties of Equality For any real numbers a , b , and c , if a = b, then a = b + c + c a = b - c - c Example: If x – 4 = 5, then x – 4 = 5 + 4 + 4 Solving Equations

25. Sometimes an equation can be solved by adding the same number to each side or by subtracting the same number from each side or by multiplying or dividing each side by the same number. Addition and Subtraction Properties of Equality For any real numbers a , b , and c , if a = b, then a = b + c + c a = b - c - c Example: If x – 4 = 5, then x – 4 = 5 + 4 + 4 If n + 3 = –11, then Solving Equations

26. Sometimes an equation can be solved by adding the same number to each side or by subtracting the same number from each side or by multiplying or dividing each side by the same number. Addition and Subtraction Properties of Equality For any real numbers a , b , and c , if a = b, then a = b + c + c a = b - c - c Example: If x – 4 = 5, then x – 4 = 5 + 4 + 4 If n + 3 = –11, then n + 3 = –11 – 3 – 3 Solving Equations

27. Sometimes an equation can be solved by adding the same number to each side or by subtracting the same number from each side or by multiplying or dividing each side by the same number. Solving Equations

28. Sometimes an equation can be solved by adding the same number to each side or by subtracting the same number from each side or by multiplying or dividing each side by the same number. Multiplication and Division Properties of Equality For any real numbers a , b , and c , if a = b, then Solving Equations

29. Sometimes an equation can be solved by adding the same number to each side or by subtracting the same number from each side or by multiplying or dividing each side by the same number. Multiplication and Division Properties of Equality For any real numbers a , b , and c , if a = b, then a = b · c · c Solving Equations

30. Sometimes an equation can be solved by adding the same number to each side or by subtracting the same number from each side or by multiplying or dividing each side by the same number. Multiplication and Division Properties of Equality For any real numbers a , b , and c , if a = b, then a = b · c · c a = b Solving Equations c c

31. Sometimes an equation can be solved by adding the same number to each side or by subtracting the same number from each side or by multiplying or dividing each side by the same number. Multiplication and Division Properties of Equality For any real numbers a , b , and c , if a = b, then a = b · c · c a = b Example: Solving Equations c c

32. Sometimes an equation can be solved by adding the same number to each side or by subtracting the same number from each side or by multiplying or dividing each side by the same number. Multiplication and Division Properties of Equality For any real numbers a , b , and c , if a = b, then a = b · c · c a = b Example: 4 4 Solving Equations c c

33. Sometimes an equation can be solved by adding the same number to each side or by subtracting the same number from each side or by multiplying or dividing each side by the same number. Multiplication and Division Properties of Equality For any real numbers a , b , and c , if a = b, then a = b · c · c a = b Example: 4 4 Solving Equations c c

34. Sometimes an equation can be solved by adding the same number to each side or by subtracting the same number from each side or by multiplying or dividing each side by the same number. Multiplication and Division Properties of Equality For any real numbers a , b , and c , if a = b, then a = b · c · c a = b Example: 4 4 Solving Equations c c - 3 -3

35. Java Applet – Solving Functions End of Lesson

36. Credits PowerPoint created by Using Glencoe’s Algebra 2 text, © 2005 Robert Fant