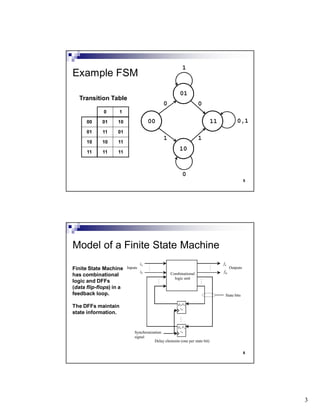
The document discusses sequential circuits and their components. It begins with an overview of sequential circuits and finite state machines. It then covers different types of flip-flops like D flip-flops and their usage. Counters and sequencers are presented as examples of sequential circuits. Details about designing a 3-bit up counter like its state table and logic equations are provided. Finally, registers are discussed including an example of a 4-bit register with parallel load.

1. 1
1
Today: Sequential Circuits
(H&H 3.1-3.6, 5.4)
Next: continued
Lecture Topics
2
Self-study module #2 (this week)
Project #1 scores sent via email yesterday
Project #2 (due no later than 9/12)
Project #3 (due no later than 9/19)
Announcements

2. 2
3
• Combinational circuits have no "memory":
the output is determined by the current
inputs.
• Sequential circuits "remember" the current
state: the output is determined by the
current inputs and the current state.
Sequential Circuits
4
• A vending machine must remember how many
coins and what kinds of coins have been inserted.
The behavior is based not only on the current coin
inserted (current input), but also on how many and
what kinds of coins have been inserted previously
(current state).
• These are referred to as finite state machines
(finite state automata).
Example: vending machine

3. 3
5
Example FSM
Transition Table
0 1
00 01 10
01 11 01
10 10 11
11 11 11
00
01
10
11
0
1
0
0,1
1
0
1
6
Model of a Finite State Machine
Finite State Machine
has combinational
logic and DFFs
(data flip-flops) in a
feedback loop.
The DFFs maintain
state information.

4. 4
7
D Flip-flop
Positive edge-triggered D flip-flop: the value of D is copied into
the flip-flop (and becomes the value of Q) when C changes
from 0 to 1.
8
Clock Waveform
• Clock pulse "edges"
Rising edge (leading edge, positive edge)
Falling edge (trailing edge, negative edge)
• A clock cycle of 25 ns equals a clock rate of 40 MHz

5. 5
9
S-R Latch
• The S input sets the latch (forces it to contain a 1)
• The R input resets the latch (forces it to contain a 0)
10
NAND and NOR Gates

6. 6
11
Four cases:
• S = 1, R = 0
• S = 0, R = 1
• S = 0, R = 0
• S = 1, R =1
Analysis: SR Latch
R
S
Q
Q
N1
N2
12
Analysis: SR Latch
if S = 1, R = 0 then
Q = 1, Q' = 0
(Set the latch)
if S = 0, R = 1 then
Q = 0, Q' = 1
(Reset the latch)
R
S
Q
Q
N1
N2
1
0
0
1
0
1
R
S
Q
Q
N1
N2
0
1
1
0
0
0
1

7. 7
13
Analysis: SR Latch
if S = 0, R = 0 then
no change to Q, Q'
(Keep previous Q)
R
S
Q
Q
N1
N2
0
0
R
S
Q
Q
N1
N2
0
0
0
Qprev
= 0 Qprev
= 1
1
14
Analysis: SR Latch
if S = 1, R = 1 then
Q = 0, Q' = 0
(Invalid!)
Cannot set and
reset the latch
simultaneously
Note: Q ≠ NOT Q'
R
S
Q
Q
N1
N2
1
1
0
0
0
0

8. 8
15
Using NOR gates
(active high)
Using NAND gates
(active low)
S-R Latch
16
Gated S-R Latch
The Enable signal
(usually a clock signal)
controls the NAND gates
(which control the S and
R inputs)

9. 9
17
Gated D Latch
Only D signal (instead of S
and R signals)
Potential problem: If D
changes while the Enable
control signal is high, the
output will also change.
18
o Output Q changes only when Clk = 1
• Q tracks D when Clk = 1
o This latch is level-sensitive since the output is
sensitive to the level of the clock
D Latch Timing Diagram
t1 t2 t3 t4
Time
Clk
D
Q

10. 10
19
Master-Slave D Flip-Flop
Want changes in Q only on the transition of the Clk signal
from 1 0 (or from 0 1)
When Clock = 1, master latch tracks D; slave latch remains
unchanged (Q remains fixed)
When Clock = 0, master latch is unchanged; slave latch tracks Qm
D Q
Q
Master Slave
D
Clock
Q
Q
D Q
Q
Q
ClkClk
D Q
Q
negative edge-triggered flip-flop
20
Timing of Master-Slave D Flip-Flop
Changes to Q occur only on the negative edge of the Clock
D Q
Q
Master Slave
D
Clock
Q
Q
D Q
Q
Q m Q s
ClkClk
D
Clock
Q m
Q Q s=

11. 11
21
Negative Edge-Triggered DFF
• When CLK is high, the
two input latches contain
0, so the Main latch
remains in its previous
state, regardless of any
changes to D.
• On the falling edge of
CLK, values in the two
input latches will affect the
state of the Main latch.
• While CLK is low, D
cannot affect the Main
latch.
22
Positive Edge-Triggered DFF
D
Clock
P4
P3
P1
P2
5
6
1
2
3
Q
Q
4

12. 12
23
Asynchronous Clear and Preset (active low)
DFF with Clear and Preset
D
Clock
Q
Q
Clear
Preset
Preset
Clear
D Q
Q
24
Commercial D Flip-flop
Q
Q
PRE
D
CLR
CLK
PRE
CLR
Q
Q
Q
Q
Asynchronous controls
(active low):
PRE' – force to 1 (preset)
CLR' – force to 0 (clear)
D
CLK

13. 13
25
Commercial D Flip-flop
PRE' CLR' D CLK Q Q' Mode
0 0 X X 1 1 Not allowed
0 1 X X 1 0 Set
1 0 X X 0 1 Clear
1 1 X 0 Qn-1 Q'n-1 Hold
1 1 X 1 Qn-1 Q'n-1 Hold
1 1 0 0 1 Clocked operation
1 1 1 1 0 Clocked operation
26
State info in FSM
o Counter
o Sequencer
Data storage
o Register with parallel load
o Register file (collection of registers)
Uses of Data Flip-flops

14. 14
27
Standard Up Counter
o Sequence starts at 0, counts up by 1
o Starts over after reaching max
Example: 2-bit Up Counter
0, 1, 2, 3, 0, 1, 2, 3, 0, …
Variations: count down, count by 2, etc.
Counters
28
Output: 000, 001, 010, 011, 100, 101, 110, 111, 000, …
3-bit Up Counter
3
Reset
Clock
Output

15. 15
29
Output: 000, 001, 010, 011, 100, 101, 110, 111, 000, …
Three DFFs used to store current state
Combinational logic used to determine next state
Reset: initialize DFFs to state 000
Clock: copy next state into DFFs
3-bit Up Counter
30
Design of 3-bit Up Counter
Three separate
functions:
N2(C2, C1, C0) = ….
N1(C2, C1, C0) = ….
N0(C2, C1, C0) = ….
C2 C1 C0 N2 N1 N0
0 0 0 0 0 1
0 0 1 0 1 0
0 1 0 0 1 1
0 1 1 1 0 0
1 0 0 1 0 1
1 0 1 1 1 0
1 1 0 1 1 1
1 1 1 0 0 0

16. 16
31
N2(C2, C1, C0) = C2C1' + C2C0' + C2'C1C0
Karnaugh Map for N2
C2C1
00 01 11 10
C0
0 0 0 1 1
1 0 1 0 1
32
N1(C2, C1, C0) = C1'C0 + C1C0'
Karnaugh Map for N1
C2C1
00 01 11 10
C0
0 0 1 1 0
1 1 0 0 1

17. 17
33
N0(C2, C1, C0) = C0'
Karnaugh Map for N0
C2C1
00 01 11 10
C0
0 1 1 1 1
1 0 0 0 0
34
Generate signals for N steps in a cycle
o N bits of output
o Exactly 1 bit asserted at each step
Example: 5-bit Sequencer
10000, 01000, 00100, 00010, 00001, 10000, …
Sequencers

18. 18
35
3-bit Sequencer
Output: 100, 010, 001, 100, 010, 001, 100, …
3
ResetClock
Output
36
3-bit Sequencer
Output: 100, 010, 001, 100, 010, 001, 100, …
Q
QB
SET
CLEAR
D Q
QB
SET
CLEAR
D Q
QB
SET
CLEAR
D
Reset
O2 O1 O0

19. 1
1
Today: Sequential Circuits
(H&H 3.1-3.6, 5.4)
Next: Integer Arithmetic
(H&H 5.1-5.2)
Lecture Topics
2
Self-study module #3
Project #3 (due no later than 9/19)
Project #4 (due no later than 9/26)
Announcements

20. 2
3
Due Thursday, 9/19 (by 11:59 PM)
Focuses on implementation of circuits you
designed for Project #2
o review handout
o review notes file
o complete Self-study Exercise #2
Computer Project #3
4
• Combinational circuits have no "memory":
the output is determined by the current
inputs.
• Sequential circuits "remember" the current
state: the output is determined by the
current inputs and the current state.
Sequential Circuits

21. 3
5
Model of a Finite State Machine
Finite State Machine
has combinational
logic and DFFs
(data flip-flops) in a
feedback loop.
The DFFs maintain
state information.
6
Commercial D Flip-flop
Q
Q
PRE
D
CLR
CLK
PRE
CLR
Q
Q
Q
Q
Asynchronous controls
(active low):
PRE' – force to 1 (preset)
CLR' – force to 0 (clear)
D
CLK

22. 4
7
Commercial D Flip-flop
PRE' CLR' D CLK Q Q' Mode
0 0 X X 1 1 Not allowed
0 1 X X 1 0 Set
1 0 X X 0 1 Clear
1 1 X 0 Qn-1 Q'n-1 Hold
1 1 X 1 Qn-1 Q'n-1 Hold
1 1 0 0 1 Clocked operation
1 1 1 1 0 Clocked operation
8
State info in FSM
o Counter
o Sequencer
Data storage
o Register with parallel load
o Register file (collection of registers)
Uses of Data Flip-flops

23. 5
9
Standard Up Counter
o Sequence starts at 0, counts up by 1
o Starts over after reaching max
Example: 2-bit Up Counter
0, 1, 2, 3, 0, 1, 2, 3, 0, …
Variations: count down, count by 2, etc.
Counters
10
Output: 000, 001, 010, 011, 100, 101, 110, 111, 000, …
3-bit Up Counter
3
Reset
Clock
Output

24. 6
11
Output: 000, 001, 010, 011, 100, 101, 110, 111, 000, …
Three DFFs used to store current state
Combinational logic used to determine next state
Reset: initialize DFFs to state 000
Clock: copy next state into DFFs
3-bit Up Counter
12
Design of 3-bit Up Counter
Three separate
functions:
N2(C2, C1, C0) = ….
N1(C2, C1, C0) = ….
N0(C2, C1, C0) = ….
C2 C1 C0 N2 N1 N0
0 0 0 0 0 1
0 0 1 0 1 0
0 1 0 0 1 1
0 1 1 1 0 0
1 0 0 1 0 1
1 0 1 1 1 0
1 1 0 1 1 1
1 1 1 0 0 0

25. 7
13
N2(C2, C1, C0) = C2C1' + C2C0' + C2'C1C0
Karnaugh Map for N2
C2C1
00 01 11 10
C0
0 0 0 1 1
1 0 1 0 1
14
N1(C2, C1, C0) = C1'C0 + C1C0'
Karnaugh Map for N1
C2C1
00 01 11 10
C0
0 0 1 1 0
1 1 0 0 1

26. 8
15
N0(C2, C1, C0) = C0'
Karnaugh Map for N0
C2C1
00 01 11 10
C0
0 1 1 1 1
1 0 0 0 0
16
Generate signals for N steps in a cycle
o N bits of output
o Exactly 1 bit asserted at each step
Example: 5-bit Sequencer
10000, 01000, 00100, 00010, 00001, 10000, …
Sequencers

27. 9
17
3-bit Sequencer
Output: 100, 010, 001, 100, 010, 001, 100, …
3
ResetClock
Output
18
3-bit Sequencer
Output: 100, 010, 001, 100, 010, 001, 100, …
Q
QB
SET
CLEAR
D Q
QB
SET
CLEAR
D Q
QB
SET
CLEAR
D
Reset
O2 O1 O0

28. 10
19
N-bit register with parallel load
o N bits of input
o N bits of output
o Input copied into register in parallel
(simultaneously, on clock pulse)
o Input becomes output
o Value retained until deliberately replaced
Registers
20
4-bit Register using DFFs
Q 3 Q 2 Q 1 Q 0
Clock
Parallel input
Parallel output
D Q
Q
D Q
Q
D Q
Q
D Q
Q

29. 11
21
4-bit Register with Load Control
Q 3 Q 2 Q 1 Q 0
Clock
Parallel input
Parallel output
D Q
Q
D Q
Q
D Q
Q
D Q
Q
Load
22
Copying a value into a register
Assume 8-bit register:
Place 8-bit value on D
Assert Load
Wait for Clock pulse
De-assert Load
D0-7 Q0-7D0-7
Q0-7
Clock
8 8
Load

30. 12
23
Register File and ALU
Register
File ALU
24
Register File
N registers
2 output ports
1 input port
Read register 1 selects
register for Read data 1
Read register 2 selects
register for Read data 2
Write register selects
register for Write data

31. 13
25
Register File
Select the two
source registers
using two banks
of multiplexers
26
Register File
Select destination
register using a
decoder

32. 14
27
Multi-bit MUX
High-level view:
32-bit 2-to-1 MUX
Implementation:
32 individual 2-to-1
MUXes controled by
same Select signal
28
We need to distinguish between three things
when talking about a data item:
Value
External representation
Internal representation
Data Representation

33. 15
29
External representations:
12 base 10
C base 16
1100 base 2
(many others)
Internal representation (in 8 bits):
00001100
Example: the value twelve
30
Computing systems can directly process:
Boolean data
Character data
Unsigned integer data
Signed integer data
Floating point data
First four processed in integer circuits, last
one processed in floating point circuits
Fundamental Data Types

34. 16
31
Only two values: false, true
Normally stored in 8-bit byte or 32-bit word:
false: 0
true: any other bit pattern
Processed as unsigned integers in circuits
Boolean Data
32
Internal representation uses a fixed number
of bits to represent each character in the set
ASCII (7 bits)
~cse320/Examples/example01.pdf
Unicode (8, 16 or 32 bits)
Character Data

35. 17
33
Character set includes characters from
typewriter keyboard:
52 letters (Latin alphabet, 26 upper and lower)
10 digits
33 symbols
33 control codes
Stored one character per 8-bit byte
ASCII
34
Upper case letters:
A 1000001
B 1000010
C 1000011
…
Y 1011001
Z 1011010
Examples

36. 18
35
Code numbers (bit patterns) used for
comparisons and sorting
Characters within sequences are in order:
Upper case letters
Lower case letters
Decimal digits
Other characters not in any logical order
Notes about ASCII
36
Processed as unsigned integers in circuits
Examples:
'A' + 1 ==> 'B'
'B' - 'A' ==> 1
'A' < 'B' ==> true
Notes about ASCII

37. 19
37
Internal representation uses a fixed number
of bits to represent each character in the set
ASCII table
~cse320/Examples/example01.pdf
Internal representation
~cse320/Examples/example02.pdf
Summary: Character Data
38
Expressed in base 2, with leading zeroes
Set of values starts at zero, limited by
number of bits available for storage
Example: 8-bit bytes
min: 00000000 0
max: 11111111 255 (28 – 1)
Unsigned Integers

38. 20
39
Assume 16 bits:
0 0000000000000000
1 0000000000000001
2 0000000000000010
3 0000000000000011
4 0000000000000100
Examples
40
Expressed in base 2, with leading zeroes
Set of values starts at zero, limited by
number of bits available for storage
Internal representation
~cse320/Examples/example03.pdf
Summary: Unsigned Integers

39. 21
41
Negative representation formed by applying
two’s complement operation to all bits in
positive representation (flip all bits, add 1)
Example (assume 8 bits):
+25 00011001
-25 11100111
Two’s Complement
42
Range (assume 8 bits):
max 01111111 +(27 – 1)
min 10000000 -(27)
One representation of zero (assume 8 bits):
+0 00000000
-0 00000000
Two’s Complement

40. 22
43
Internal representation (8 bits):
+21: 00010101
flip bits: 11101010
add 1: 1
--------
-21: 11101011
Example: -21 base 10
44
Internal representation (8 bits):
+22: 00010110
flip bits: 11101001
add 1: 1
--------
-22: 11101010
Example: -22 base 10