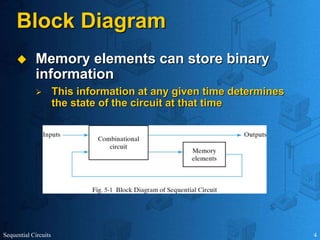
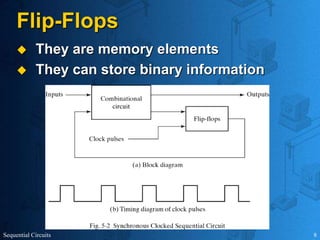
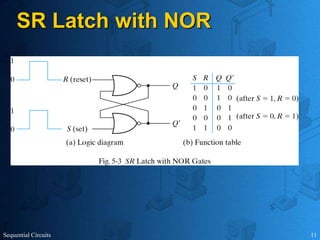
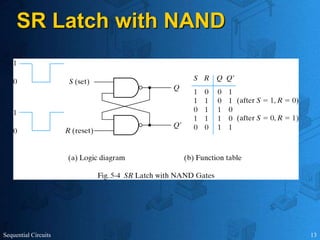
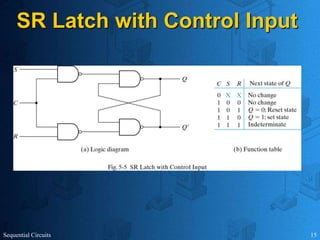
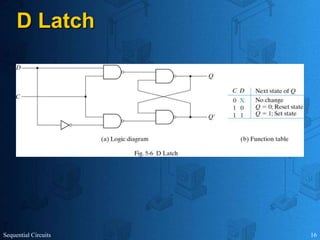
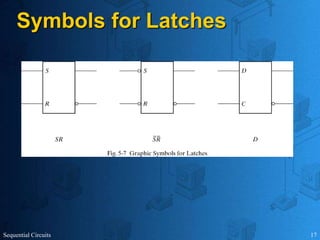
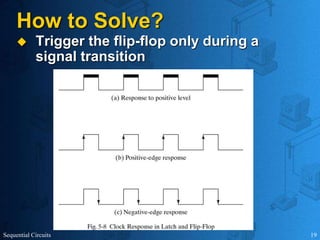
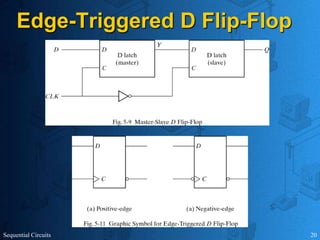
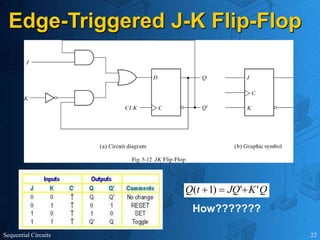
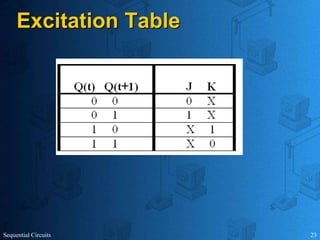
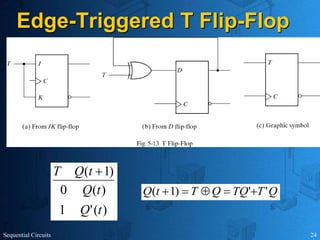
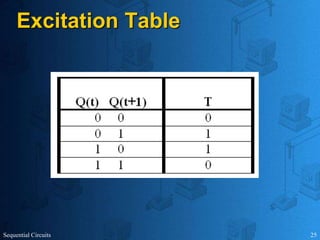
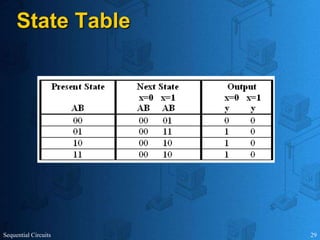
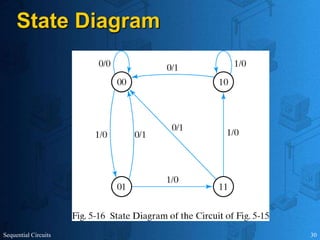
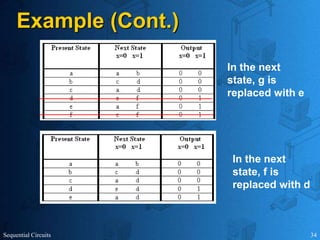
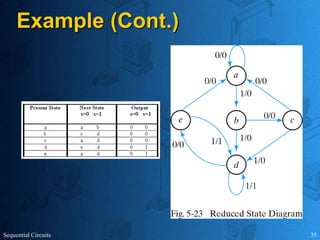
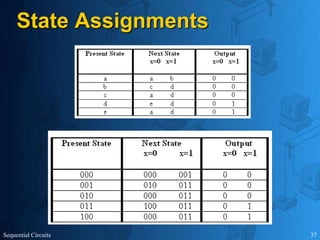
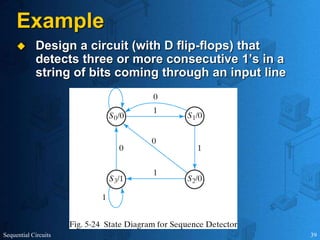
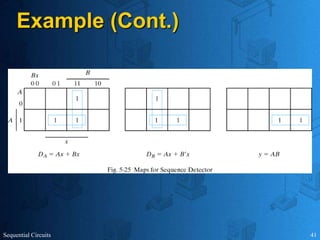
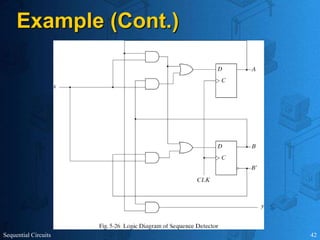
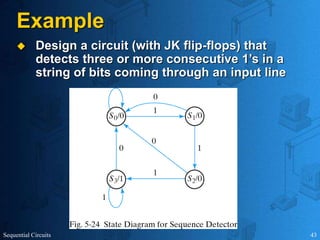
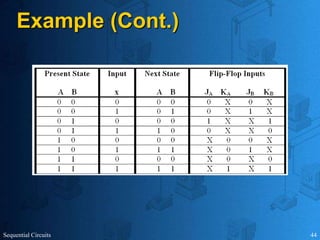
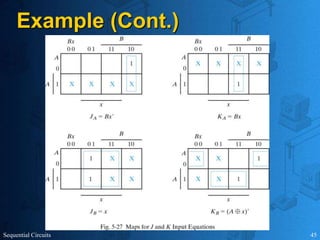
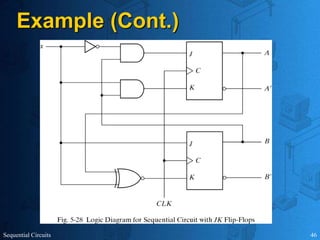
This document provides an overview of sequential circuits. It defines sequential circuits as circuits whose outputs depend on current and past input values, unlike combinational circuits whose outputs only depend on current inputs. It describes the main types of sequential circuits as synchronous (controlled by a clock) and asynchronous. Common memory elements for sequential circuits called flip-flops are introduced, including SR, D, J-K, and T flip-flops. The use of state tables and state diagrams to analyze sequential circuits is covered. Procedures for reducing states, assigning binary codes to states, and designing sequential circuits using flip-flops are also outlined. An example of designing a circuit to detect three or more consecutive 1s in an input bit string

1. Sequential Circuits 1
DIGITAL LOGIC DESIGN
by
Dr. Fenghui Yao
Tennessee State University
Department of Computer Science
Nashville, TN

2. Sequential Circuits 2
Note
 Most of the figures are from your
course book

3. Sequential Circuits 3
Sequential Circuits
 Combinational
 The outputs depend only on the current input
values
 It uses only logic gates
 Sequential
 The outputs depend on the current and past input
values
 It uses logic gates and storage elements
 Example
 Vending machine
 They are referred as finite state machines since
they have a finite number of states

4. Sequential Circuits 4
Block Diagram
 Memory elements can store binary
information
 This information at any given time determines
the state of the circuit at that time

5. Sequential Circuits 5
Sequential Circuit Types
 Synchronous
 The circuit behavior is determined by the signals
at discrete instants of time
 The memory elements are affected only at
discrete instants of time
 A clock is used for synchronization
 Memory elements are affected only with the
arrival of a clock pulse
 If memory elements use clock pulses in their
inputs, the circuit is called
 Clocked sequential circuit

6. Sequential Circuits 6
Sequential Circuit Types
 ASynchronous
 The circuit behavior is determined by the signals
at any instant of time
 It is also affected by the order the inputs change

7. Sequential Circuits 7
Clock
 It emits a series of pulses with a
precise pulse width and precise
interval between consecutive pulses
 Timing interval between the
corresponding edges of two
consecutive pulses is known as the
clock cycle time, or period

8. Sequential Circuits 8
Flip-Flops
 They are memory elements
 They can store binary information

9. Sequential Circuits 9
Flip-Flops
 Can keep a binary state until an input
signal to switch the state is received
 There are different types of flip-flops
depending on the number of inputs
and how the inputs affect the binary
state

10. Sequential Circuits 10
Latches
 The most basic flip-flops
 They operate with signal levels
 The flip-flops are constructed from
latches
 They are not useful for synchronous
sequential circuits
 They are useful for asynchronous
sequential circuits

11. Sequential Circuits 11
SR Latch with NOR

12. Sequential Circuits 12
SR Latch with NOR
1
R
1,
S
avoid
,
conditions
normal
In
0
set to
are
Q'
and
Q
undefined,
1
R
1,
S
state
reset
1
'
,
0
state
set
0
'
,
1













Q
Q
Q
Q
reset
R
set
S

13. Sequential Circuits 13
SR Latch with NAND

14. Sequential Circuits 14
SR Latch with NAND
0
R
0,
S
avoid
,
conditions
normal
In
1
set to
are
Q'
and
Q
undefined,
0
R
0,
S
state
reset
0
'
,
1
state
set
1
'
,
0













Q
Q
Q
Q
reset
R
set
S

15. Sequential Circuits 15
SR Latch with Control Input

16. Sequential Circuits 16
D Latch

17. Sequential Circuits 17
Symbols for Latches

18. Sequential Circuits 18
Note
 The control input changes the state of
a latch or flip-flop
 The momentary change is called a
trigger
 Example: D Latch
 It is triggered every time the pulse goes to the
logic level 1
 As long as the pulse remains at the logic level 1,
the change in the data (D) directly affects the
output (Q)
 THIS MAY BE A BIG PROBLEM since the state of
the latch may keep changing depending on the
input (may be coming from a combinational logic
network)

19. Sequential Circuits 19
How to Solve?
 Trigger the flip-flop only during a
signal transition

20. Sequential Circuits 20
Edge-Triggered D Flip-Flop

21. Sequential Circuits 21
Characteristics of D Flip-
Flop
D
t
Q 
 )
1
(

22. Sequential Circuits 22
Edge-Triggered J-K Flip-Flop
Q
K
JQ
t
Q '
'
)
1
( 


How???????

23. Sequential Circuits 23
Excitation Table

24. Sequential Circuits 24
Edge-Triggered T Flip-Flop
Q
T
TQ
Q
T
t
Q '
'
)
1
( 




)
(
'
1
)
(
0
)
1
(
t
Q
t
Q
t
Q
T 

25. Sequential Circuits 25
Excitation Table

26. Sequential Circuits 26
Direct Inputs
 You can use asynchronous inputs to
put a flip-flop to a specific state
regardless of the clock
 You can clear the content of a flip-flop
 The content is changed to zero (0)
 This is called clear or direct reset
 This is particularly useful when the power is off
 The state of the flip-flop is set to unknown

27. Sequential Circuits 27
D Flip-Flop with
Asynchronous Reset

28. Sequential Circuits 28
State Equations
 
'
)
(
'
)
1
(
)
1
(
)
(
'
)
(
)
(
)
(
)
(
)
(
'
)
1
(
)
(
)
(
)
(
)
(
)
1
(
x
B
A
y
x
A
t
B
Bx
Ax
t
A
t
x
t
B
t
A
t
y
t
x
t
A
t
B
t
x
t
B
t
x
t
A
t
A














A state equation shows
the next state as a
function of the current
state and inputs

29. Sequential Circuits 29
State Table

30. Sequential Circuits 30
State Diagram

31. Sequential Circuits 31
Analysis with D Flip-Flops
y
x
A
t
A
y
x
A
DA







)
1
(

32. Sequential Circuits 32
State Reduction
 Reduce the number of states but keep
the input-output requirements
 Reducing the number of states may
reduce the number of flip-flops
 If there are n flip-flops, there are 2^n states
 If you have two circuits that produce
the same output sequence for any
given input sequence, the two circuits
are equivalent
 They may replace each other

33. Sequential Circuits 33
State Reduction Example
Find the states for which the
next states and outputs are
the same

34. Sequential Circuits 34
Example (Cont.)
In the next
state, g is
replaced with e
In the next
state, f is
replaced with d

35. Sequential Circuits 35
Example (Cont.)

36. Sequential Circuits 36
State Assignment
 You need to assign binary values for
each state so that they can be
implemented
 You need to use enough number of
bits to cover all the states

37. Sequential Circuits 37
State Assignments

38. Sequential Circuits 38
Design Procedure
 Derive a state diagram
 Reduce the number of states
 Assign binary values to the states
 Obtain binary coded state table
 Choose the type of flip-flop to be used
 Derive simplified flip-flop input
equations and output equations
 Draw the logic diagram

39. Sequential Circuits 39
Example
 Design a circuit (with D flip-flops) that
detects three or more consecutive 1’s in a
string of bits coming through an input line

40. Sequential Circuits 40
Example (Cont.)
 
 
 










7
,
6
)
,
,
(
7
,
5
,
1
)
,
,
(
)
1
(
7
,
5
,
3
)
,
,
(
)
1
(
x
B
A
y
x
B
A
D
t
B
x
B
A
D
t
A
B
A

41. Sequential Circuits 41
Example (Cont.)

42. Sequential Circuits 42
Example (Cont.)

43. Sequential Circuits 43
Example
 Design a circuit (with JK flip-flops) that
detects three or more consecutive 1’s in a
string of bits coming through an input line

44. Sequential Circuits 44
Example (Cont.)

45. Sequential Circuits 45
Example (Cont.)

46. Sequential Circuits 46
Example (Cont.)

47. Sequential Circuits 47
Study Problems
 Course Book Chapter – 5 Problems
 5 – 3
 5 – 5
 5 – 6
 5 – 7
 5 – 10
 5 – 12
 5 – 13
 5 – 19

48. Sequential Circuits 48
Questions