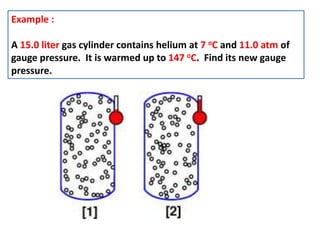
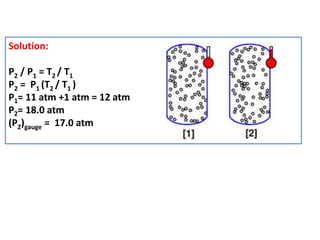
This document discusses the expansion of gases and the relationships between pressure, volume, temperature, and number of moles in gases. It introduces the ideal gas law (PV=nRT) and describes some key gas processes including isobaric (constant pressure), isothermal (constant temperature), and isometric (constant volume) processes. Examples are provided to demonstrate how to use the ideal gas law and gas equations of state to calculate pressure, volume, temperature, or number of moles given values of the other variables.

1. Chapter 14
Expansion of Gases
Younes Sina

2. For a gas, molecules are free to move and bounce repeatedly against each
other as well as their container's walls. In each collision, a gas molecule
transfers some momentum to its container's walls. Gas pressure is the result
of such momentum transfers. The faster they move, the greater impulse per
collision they impart to the container's walls causing a higher pressure. For a
fixed volume, if the temperature of a gas increases (by heating), its pressure
increases as well. This is simply because of increased kinetic energy of gas
molecules that cause more number of collisions per second and therefore
increased pressure.
The thermal expansion of a gas involves 3 variables:
Volume
Temperature
Pressure
Pressure is the result of the collision of its molecules on the walls of that container.
Temperature is a result of the vibrations of its atoms and molecules. It is an indicator
of kinetic energy of the gas molecules.

3. The average K.E. of gas molecules is a function of temperature only.
(K.E.)avg = (3/2) kT
absolute temperature in Kelvin
Boltzmann's constant (k = 1.38x10-23 J /K)
K.E. = (1/2)MV2
average speed of gas molecules
Mass of gas molecules

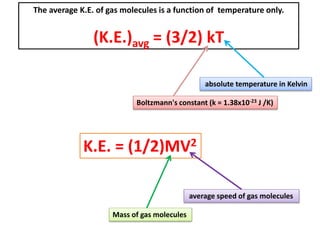
4. Example :
a) Calculate the average K.E. of air molecules at 27.0 oC.
b) Calculate the average speed of its constituents (oxygen molecules and
nitrogen molecules).
1 mole of O2 = 32.0 grams= 6.02x1023 molecules of O2
1 mole of N2 = 28.0 grams= 6.02x1023 molecules of N2
Solution:
K.E. = (3/2) k T
K.E. = (3/2) (1.38x10-23 J/K)(27+273)K = 6.21x10-21 J/molecule
(Every gas molecule at this temperature, has 6.21x10-21 J whether it is a
single O2 molecule or a single N2 molecule).
For every O2 molecule: K.E. = (1/2)MV2
6.21x10-21 J = (1/2) [ 32.0x10-3 kg / 6.02x1023]V2 → V = 483m/s
For every N2 molecule: K.E. = (1/2)MV2
6.21x10-21 J = (1/2) [ 28.0x10-3 kg / 6.02x1023 ]V2 → V = 517m/s
Each N2 molecule is lighter; therefore, its average speed is
higher. Each O2 molecule is heavier; therefore, its average speed is lower at
the same temperature.

5. Expansion of Gases
Perfect Gas Law:
PV = nRT
gas absolute pressure
V is its volume (the volume of its container)
Universal gas constant = 8.314 [J/(mole K)]
gas absolute temperature in Kelvin
The two conditions for a gas to be ideal or obey this equation are:
1) The gas pressure should not exceed about 8 atmospheres.
2) The gas must be superheated (gas temperature sufficiently
above its boiling point) at the operating pressure and volume.
number of moles of gas
Equation of State

6. The Unit of " PV ":
Note that the product " PV " has dimensionally the unit of "energy “.
In SI, the unit of "P" is [ N / m2 ] and the unit of volume " V " is [ m3 ].
On this basis, the unit of the product " PV " becomes [ Nm ] or [ Joule ].
The " Joule " that appears in R = 8.314 J /(mole K) is for this reason.
Example :
A 0.400 m3 tank contains nitrogen at 27 oC. The pressure gauge on it reads
3.75 atmosphere. Find
(a) the number of moles of gas in the tank
(b) its mass in kg.

7. Solution:
Pabs. = Pgauge + 1 atm = 4.75 atm
Tabs. = 27oC + 273 = 300K
PV = nRT → n = (PV) / [RT]
n = (4.75x101000Pa)(0.400m3) / [(8.314 J / (mole K))300K]
(a) n = 76.9 moles
(b) M = (76.9 moles)(28.0 grams /mole) = 2150 grams = 2.15 kg

8. Example :
A 0.770 m3 hydrogen tank contains 0.446 kg of hydrogen at 127 oC.
The pressure gage on it is not working. What pressure should the gauge show?
Each mole of H2 is 2.00 grams.
Solution:
n = (0.446x103 grams) / (2.00 grams / mole) = 223 moles
PV = nRT → P = (nRT) / V
P = (223 moles)[ 8.314 J/(mole K)] (127 + 273)K / (0.770 m3)
Pabs = 963,000 Pa
Pgauge = Pabs - 1atm = 963,000 Pa - 101,000Pa = 862,000Pa (≈ 8.6 atm)

9. For a fixed mass of a gas:
P1V1 = nRT1→ n= P1V1/ RT1
P2V2 = nRT2→ n= P2V2/ RT2
(P1V1) / (P2V2) = T1 / T2
P1V1/ RT1= P2V2/ RT2
(P1V1)/ T1= (P2V2)/ T2

10. Example :
1632 grams of oxygen is at 2.80 atm. of gauge pressure and a temperature
of 127 oC. Find
a) its volume
It is then compressed to 6.60 atm. of gauge pressure while cooled down
to 27 oC. Find
(b) its new volume
Solution:
n = (1632 / 32.0) moles = 51.0 moles
(a) PV = nRT → V = nRT/p
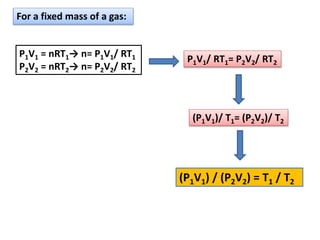
V = (51.0moles)[(8.314 J/(mole K)](127+273)K /(3.80x101,000)Pa = 0.442m3
(b) (P2V2)/(P1V1) =T2 /T1
(7.6atm)(V2) /[(3.8atm)(0.442m3)] = 300K/400K
V2 = 0.166m3

11. Constant Pressure (Isobar) Processes:
A process in which the pressure of an ideal gas does not change is called an
" isobar" process.
Constant pressure means P2=P1
(P2V2) / (P1V1) = T2 / T1 → V2 / V1 = T2 / T1
Example :
A piston-cylinder mechanism as shown below
may be used to keep a constant pressure. The
pressure on the gas under the piston is 0 gauge
plus the extra pressure that the weight
generates. Let the piston's radius be 10.0 cm
and the weight 475 N, and suppose that the
position of the piston at 77 oC is 25.0 cm from
the bottom of the cylinder. Find its position
when the system is heated and the
temperature is 127 oC.

12. Solution:
V1 = πr2h1 = π(10.0cm)2(25.0 cm) = 2500π cm3
V2 = πr2h2 = π(10.0cm)2( h2 ) = (100π)h2 cm3
P2= P1= Constant
T1 = 77 oC + 273 oC = 350 K
T2 = 127oC + 273oC = 400 K
V2 / V1 = T2 / T1
(100πh2)/(2500π) = 400/350
h2 = 28.6cm

13. Constant Temperature (Isothermal) Processes:
A process in which the temperature of a gas does not change is called
an "isothermal process“.
Constant temperature means T2=T1
Equation (P2V2) / (P1V1) = T2 / T1 becomes:
(P2V2) /(P1V1) = 1
P2V2 = P1V1
Example :
A piston cylinder system has an initial volume of 420 cm3 and the air in it is at a
pressure of 3.00 atmospheres as its gauge shows. The gas is compressed to a
volume of 140 cm3 by pushing the piston. The generated heat is removed by
enough cooling such that the temperature remains constant.
Find the final pressure of the gas.
140 cm3
420 cm3
3.00 atm
? atm
T2=T1

14. Solution:
P2V2 = P1V1
P2(140 cm3) = (4.00 atm)(420 cm3)
(P2)abs. = 12.0 atm
(P2)gauge = 11.0 atm
Constant Volume (Isometric) Processes:
A process in which the volume of an ideal gas does not change is called an
" isometric process“.
V2=V1
Equation (P2V2) / (P1V1) = T2 / T1 becomes:
P2 / P1 = T2 / T1
Rigid gas cylinders have constant volumes

15. Example :
A 15.0 liter gas cylinder contains helium at 7 oC and 11.0 atm of
gauge pressure. It is warmed up to 147 oC. Find its new gauge
pressure.

16. Solution:
P2 / P1 = T2 / T1
P2 = P1 (T2 / T1 )
P1= 11 atm +1 atm = 12 atm
P2= 18.0 atm
(P2)gauge = 17.0 atm

17. Homework:
Problems 4, 5, 6