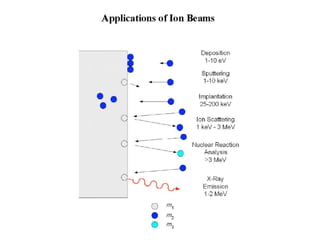
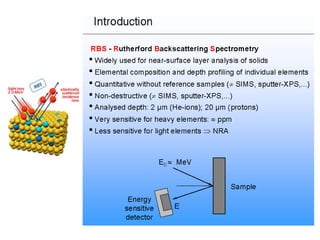
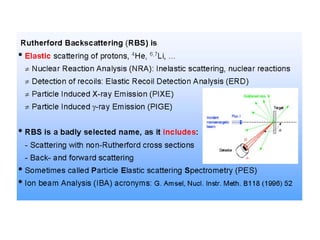
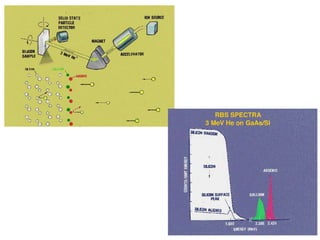
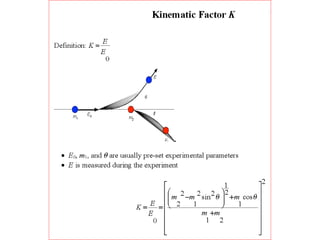
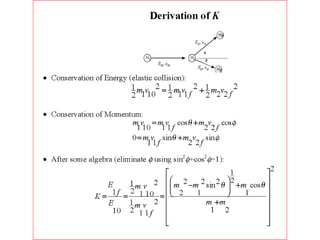
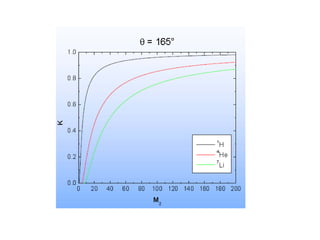
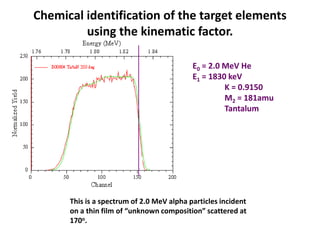
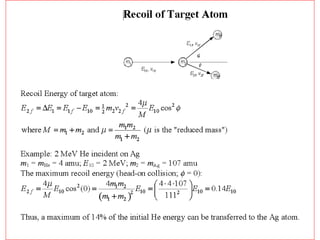
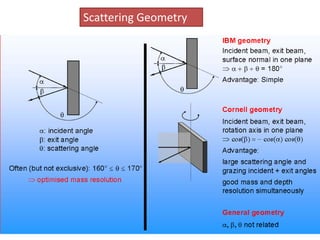
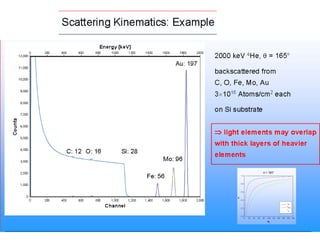
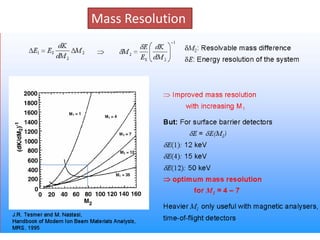
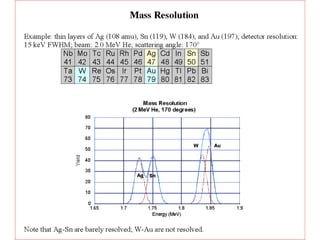
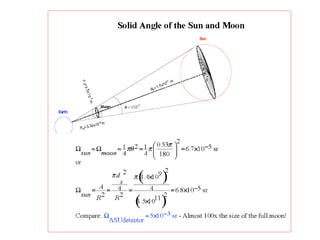
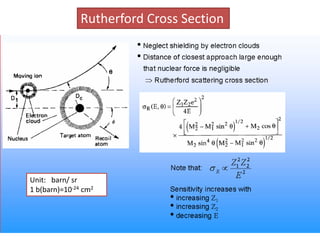
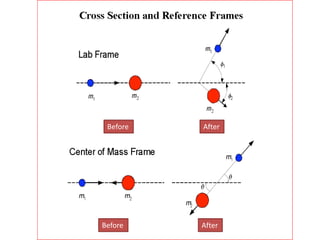
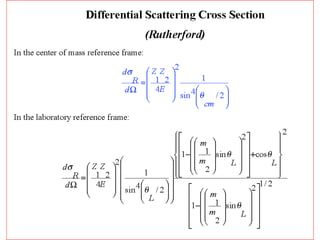
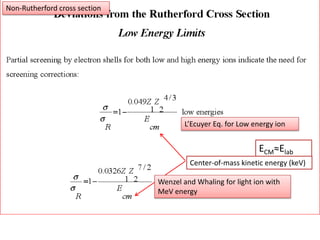
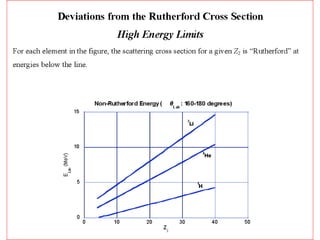
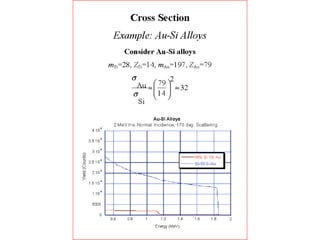
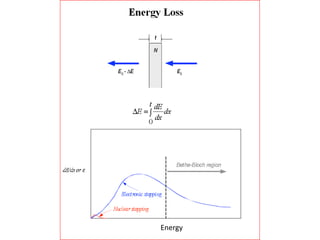
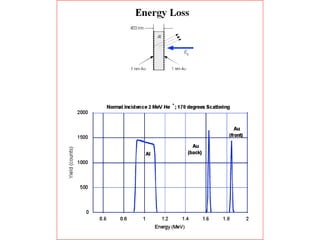
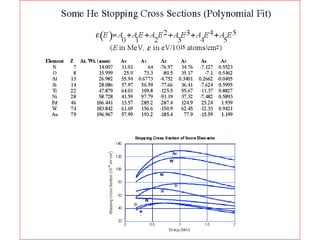
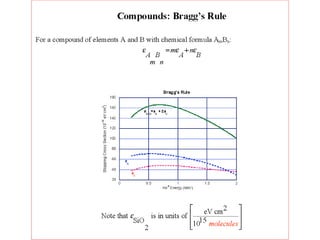
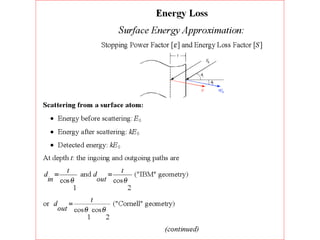
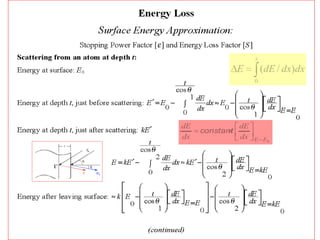
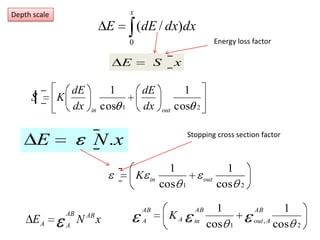
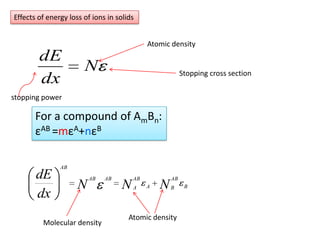
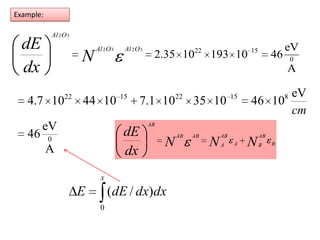
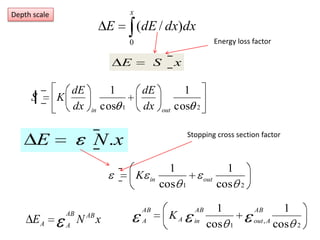
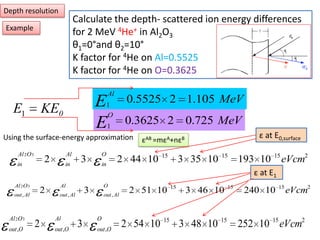
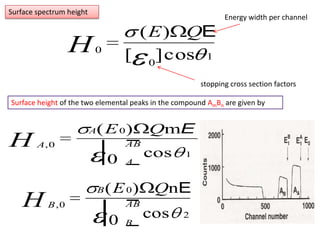
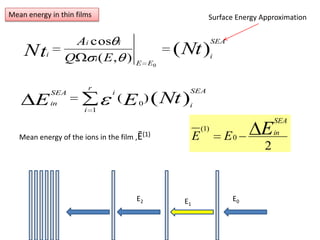
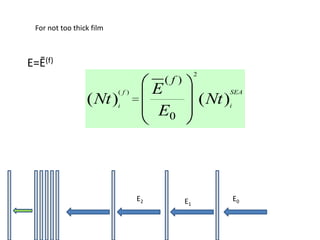
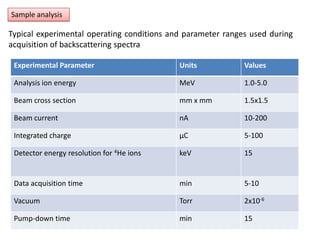
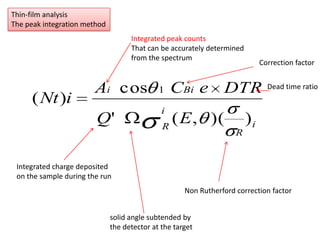
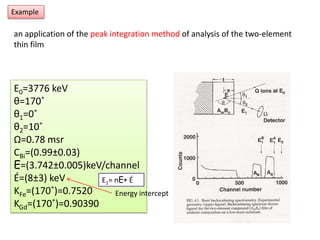
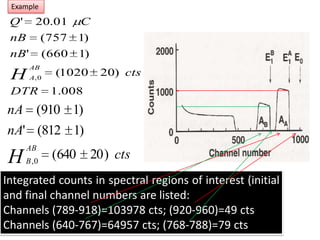
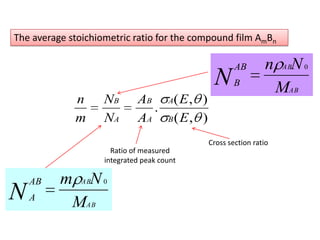
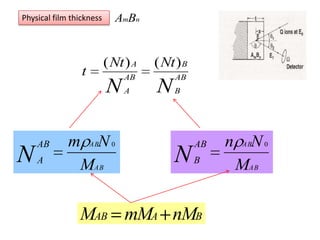
This document discusses backscattering spectrometry, which uses elastic scattering of ions to determine the elemental composition of materials. It describes how Rutherford scattering can be used for low energy particles, while higher energies require solving the Schrodinger equation. Examples are given of using kinematic factors to identify elements in a spectrum and calculating stopping power and cross sections. The document outlines approaches for thin film analysis using peak integration and mean energy calculations to determine areal densities and stoichiometry.

1. Backscattering SpectrometryThe University of Tennessee, Knoxville Younes Sina

6. Rutherford scattering is also sometimes referred to as Coulomb scatteringbecause it relies only upon static electric (Coulomb) forces, and the minimal distance between particles is set only by this potential. Elastic Backscattering Spectrometry (EBS) (non-Rutherford) is used when the incident particle is going so fast that it exceeds the “Coulomb barrier" of the target nucleus, which therefore cannot be treated by Rutherford’s approximation of a point charge. In this case Schrödinger's equation should be solved to obtain the scattering cross-section.

12. Chemical identification of the target elements using the kinematic factor.E0 = 2.0 MeV HeE1 = 1830 keV K = 0.9150 M2 = 181amu TantalumThis is a spectrum of 2.0 MeV alpha particles incident on a thin film of “unknown composition” scattered at 170o.

14. Scattering Geometry

16. Mass Resolution

22. Rutherford Cross SectionUnit: barn/ sr1 b(barn)=10-24 cm2

23. BeforeAfterBeforeAfter

26. Non-Rutherford cross sectionL’Ecuyer Eq. for Low energy ion ECM≈ElabCenter-of-mass kinetic energy (keV)Wenzel and Whaling for light ion with MeV energy

31. Energy

37. E’

39. Depth scaleEnergy loss factorStopping cross section factor

41. Examples

42. Effects of energy loss of ions in solidsAtomic densityStopping cross sectionstopping power For a compound of AmBn:εAB =mεA+nεBAtomic densityMolecular density

43. Calculate the stopping cross section and stopping power of 2 MeV 4He+ in Al2O3 using Bragg ruleExample:εAl= 44x10-15 eVcm2εO= 35x10-15 eVcm2From appendix 3:For a compound of AmBn:εAB =mεA+nεBεAl2O3=(2x44+3x35)x10-15 =193x10-15eVcm2

44. Example:

45. Depth scaleEnergy loss factorStopping cross section factor

46. Depth resolutionCalculate the depth- scattered ion energy differences for 2 MeV 4He+ in Al2O3θ1=0°and θ2=10°K factor for 4He on Al=0.5525K factor for 4He on O=0.3625Exampleε at E0,surfaceUsing the surface-energy approximationεAB =mεA+nεBε at E1

47. ExampleWe can now calculate the stopping cross section factorsUsing the molecular density N Al2O3=2.35x1022 molecules/cm3we find:

48. Surface spectrum heightEnergy width per channelstopping cross section factorsSurface height of the two elemental peaks in the compound AmBn are given by

49. Mean energy in thin filmsSurface Energy ApproximationMean energy of the ions in the film ,Ē(1)E0E2E1

50. Mean energy in thin filmsFor the second iteration, the values of (Nt)i(1) should be calculated using with E= Ē(1) then ∆Ei(1) and Ē(2)E0E2E1

51. ExampleCalculate surface height for 2 MeV 4He+ on Al2O3:Ω=10-3srE=1keV/channelQ=6.24x1013 incident particles (10μC charge)θ1=0°, θ2=10° (scattering angle=170°)From appendix 6: σRAl=0.2128x10-24 & σRO=0.0741x10-24 From previous example:

52. For not too thick filmE=Ē(f)E0E2E1

53. Sample analysisTypical experimental operating conditions and parameter ranges used during acquisition of backscattering spectra

54. Thin-film analysisThe peak integration methodIntegrated peak countsThat can be accurately determined from the spectrumCorrection factorDead time ratioIntegrated charge deposited on the sample during the runNon Rutherford correction factorsolid angle subtended by the detector at the target

55. Example an application of the peak integration method of analysis of the two-element thin filmE0=3776 keVθ=170˚θ1=0˚θ2=10˚Ω=0.78 msrCBi=(0.99±0.03)E=(3.742±0.005)keV/channelÉ=(8±3) keVKFe=(170˚)=0.7520KGd=(170˚)=0.90390E1= nE+ ÉEnergy intercept

56. Example From appendix 6 FromCenter-of-mass energy

57. Example From Trim 1985:

58. Example Integrated counts in spectral regions of interest (initial and final channel numbers are listed:Channels (789-918)=103978 cts; (920-960)=49 ctsChannels (640-767)=64957 cts; (768-788)=79 cts

59. Example From: E1= nE+ É and Ki=Ei1/E0 : Energy interceptTherefore, element A and B are Gd and Fe, respectively. Note that element A could also be Tb, because KTb=0.9048

60. Example Calculation of elemental areal densities,(Nt)Values of Ai are calculated from the integrated counts in the regions of interestsIn this case, the background correction is almost negligible

61. Example The areal densities in the surface-energy approximation,(Nt)SEAi using E=E010.998DTRCBiAieQ’Ωσ

62. Example The mean energy of the 4He ion in the film, Ē(1), is calculated (to first order) using the following equation For the first-order energy loss, ΔESEAin ,of the ions in the film:

63. Example From the following Eq. we can calculate the areal densities:

64. Results of an additional iteration of this procedure using the following equations we have: (Note that Feand Gdare evaluated at Ē(1))Example

65. Example The average stoichiometric ratio for this film using the following Eq.:

66. Example If the molecular formula for the film is written as GdmFen , then:m=0.209±0.001 and n=0.791±0.001n+m=1

67. The value of the physical film thickness:Example Elemental bulk density

68. Areal densityIntegrated peak countAreal density, Nt, as atoms per unit area Cross sectionIncident ionsDetector solid angle

69. The average stoichiometric ratio for the compound film AmBnCross section ratioRatio of measured integrated peak count

70. Physical film thickness

71. My hometown Mahabad, Iran