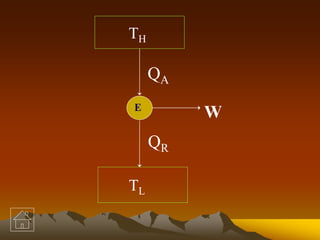
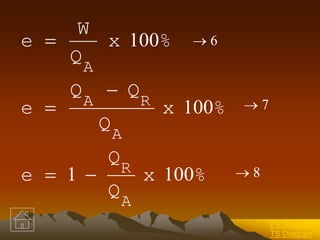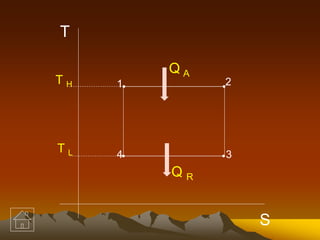
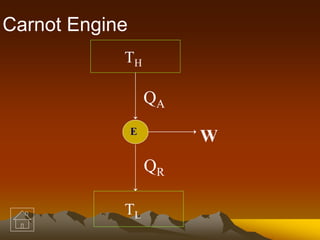
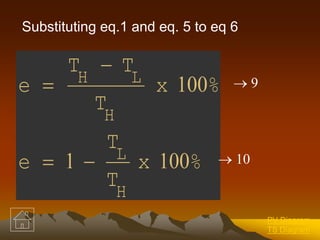
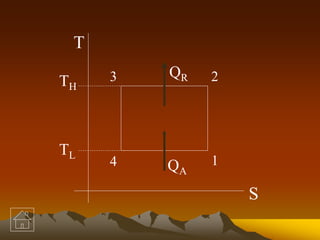
Here are the key steps to solve this problem: 1. Given: TH = 817°C = 817 + 273 = 1090 K TL = 25°C = 25 + 273 = 298 K QR = 25 kW 2. Use the Carnot efficiency equation: η = (TH - TL)/TH = (1090 - 298)/1090 = 0.726 3. Set up an equation for the heat input using the efficiency and heat rejected: QA = QR/(1-η) = 25000/(1-0.726) = 87500 kW Therefore, the heat input (QA) required is 87500 kW.

1. THERMODYNAMICS
By. Engr. Yuri G. Melliza
Thermodynamics is a science that deals with
energy transformation, the conversion of one form
of energy to another. This word was derived from a
Greek Word “Therme” that means heat and
“Dynamis” that means strength.

2. Terms and Definition
• A system is that portion in the universe, an atom, a
galaxy, a certain quantity of matter or a certain volume
in space in which one wishes to study. It is a region
enclosed by an specified boundary, that either
imaginary, fixed or moving.
• Open System: A system open to matter flow or a
system in which there an exchange of mass between
the system and the surroundings.
• Closed System: A system closed to matter flow, a
system in which there is no exchange of mass between
the system and the surrounding.
SYSTEM

3. Example : Open System (Steam Turbine)
Steam in
Steam out
Work
Boundary
Surroundings or
Environment

4. Example: Closed System (Piston in Cylinder)
system
Boundary
Surroundings
Cylinder
Piston

5. Surroundings or Environment: The region all about the system
Fluid: A substance capable of flowing and having particles which easily
move and change their relative position without the separation of mass.
Example: water, oil, steam
Working Substance: A substance responsible for the transformation of
energy.
Example: 1. Steam in a steam turbine
2. Water in a water pump
3. Air and fuel in an internal combustion engine
Pure Substance: A substance that is homogeneous in nature and is
homogeneous. It is a substance that is not a mixture of different species.
Example: Water

6. Property: Is a characteristic quality of a certain substance. by knowing the
properties of a certain substance, its state or condition may be determine.
Certain group of state of a substance are called Phases of a substance.
Intensive Properties: are properties that are independent of the mass.
Such as temperature and pressure.
Extensive Properties: are properties that are dependent upon the mass
of the system and are total values such as Volume and Total Internal
Energy.
Phases Of A Substance:
a) Solid
b) Liquid
c) Gaseous or Vapor

7. Specific Terms To Characterized Phase Transition
1) SOLIDIFYING OR FREEZING - Liquid to Solid
2) MELTING - Solid to Liquid
3) VAPORIZATION - Liquid to Vapor
4) CONDENSATION - Vapor to Liquid
5) SUBLIMATION - a change from solid directly to
vapor phase without passing the liquid phase.
Mass : It is the absolute quantity of matter in it.
m - mass in kg
Acceleration : it is the rate of change of velocity with respect
to time t.
a = dv/dt m/sec2
Velocity: It is the distance per unit time.
v = d/t m/sec

8. Force - it is the mass multiplied by the acceleration.
F = ma/1000 KN
1 kg-m/sec2 = Newton (N)
1000 N = 1 Kilo Newton (KN)
Newton - is the force required to accelerate 1 kg mass at the rate of 1 m/sec
per second.
1 N = 1 kg-m/sec2
From Newton`s Law Of Gravitation: The force of attraction between two
masses m1 and m2 is given by the equation:
Fg = Gm1m2/r2 Newton
Where: m1 and m2 - masses in kg
r - distance apart in meters
G - Gravitational constant in N-m2/kg2
G = 6.670 x 10 -11 N-m2/kg2
WEIGHT - is the force due to gravity.
W = mg/1000 KN
Where: g - gravitational acceleration at sea level, m/sec2
g = 9.81 m/sec2

9. 3
m
kg
V
mρ 
PROPERTIES OF FLUIDS
Where:  - density in kg/m3
m - mass in kg
V – volume in m3
Specific Volume () - it is the volume per unit mass or the
reciprocal of its density.
kg
m
m
V
3
υ 
kg
m3
ρ
1υ 
Density () - it is the mass per unit volume.

10. Specific Weight () - it is the weight per unit volume.
3
3
m
KN
m
KN
1000V
mg
γ
V
W
γ


Where:  - specific weight in KN/m3
m – mass in kg
V – volume in m3
g – gravitational
At standard condition:
g = 9.81 m/sec2

11. Specific Gravity Or Relative Density (S):
FOR LIQUIDS: Its specific gravity or relative density is equal tothe ratio of its
density to that of water at standard temperature and pressure.
w
L
w
L
L
γ
γ
ρ
ρ
S 
FOR GASES: Its specific gravity or relative density is equal to theratio of its
density to that of either air or hydrogen at some specified temperature and
pressure
ah
G
G
ρ
ρ
S 
Where at standard condition:
w = 1000 kg/m3
w = 9.81 KN/m3

12. Temperature: It is the measure of the intensity of heat in a body.
Fahrenheit Scale:
Boiling Point = 212 F
Freezing Point = 32 F
Centigrade or Celsius Scale:
Boiling Point = 100 C
Freezing Point = 0 C
Absolute Scale:
R = F + 460 (Rankine)
K = C + 273 (Kelvin)
32F8.1F
8.1
32F
C
Conversion




13. Pressure: It is the normal component of a force per unit area.
KPaor
2m
KN
A
F
P 
Where: P – pressure in KN/m2 or KPa
F – normal force in KN
A – area in m2
1 KN/m2 = 1 KPa (KiloPascal)
1000 N = 1 KN
If a force dF acts on an infinitesimal area dA, the intensity of Pressure is;
KPaor
2m
KN
dA
dF
P 

14. Pascal’s Law: At any point in a homogeneous fluid at rest the pressures are
the same in all directions:
y
x
z
A
B
C

P1A1
P2A2
P3A3

15. Fx = 0
From Figure:
P1A1 - P3 A3sin = 0
P1A1 = P3A3sin  Eq.1
P2A2 - P3A3cos = 0
P2A2 = P3A3 cos  Eq.2
sin = A1/A3
A1 = A3sin  Eq.3
cos = A2/A3
A2 = A3cos  Eq.4
substituting eq. 3 to eq. 1 and eq.4 to eq.2
P1 = P2 = P3

16. Atmospheric Pressure (Pa):It is the average pressure exerted by
the atmosphere.
At sea level
Pa = 101.325 KPa
= 0.101325 MPa
= 1.01325 Bar
= 760 mm Hg
= 10.33 m of water
= 1.033 kg/cm2
= 14.7 lb/in2
Pa = 29.921 in Hg
= 33.88 ft. of water
100 KPa = 1 Bar
1000 KPa = 1 MPa

17. Absolute and Gauge Pressure
Absolute Pressure: It is the pressure measured referred to
absolute zero using absolute zero as the base.
Gauge Pressure: it is the pressure measured referred to the
existing atmospheric pressure and using atmospheric pressure as
the base.
Pgauge – if it is above atmospheric
Pvacuum – negative gauge or vacuum if it is below
atmospheric
Barometer: An instrument used to determine the absolute
pressure exerted by the atmosphere

18. Atmospheic pressure (Pa)
Absolute Zero
Pvacuum
Pgauge
Pabsolute
Pabsolute
Pabs = Pgauge + Pa
Pabs = Pvacuum - Pa

19. VARIATION OF PRESSURE
PA
(P + dP)A
W
dh
F = 0
(P + dP)A - PA - W = 0
PA + dPA - PA - W = 0
dPA - W = 0 or dPA = W  Eq. 1
but : W = dV
dPA = - dV

20. where negative sign is used because distance h is measured upward and W
is acting downward.
dV = Adh then dPA = -Adh, therefore
dP = - dh
(Note: h is positive when measured upward and negative if measured
downward)

21. MANOMETERS
Manometer is an instrument used in measuring gage pressure in length of
some liquid column.
1. Open Type Manometer : It has an atmospheric surface and is capable in
measuring gage pressure.
2. Differential Type Manometer : It has no atmospheric surface and is
capable in measuring differences of pressure.
Open Type
Open end
Manometer Fluid

22. Differential Type
Fluid A
Fluid B
Fluid C

23. Second Law of
THERMODYNAMICS
• Second Law of Thermodynamics
• Kelvin – Planck Statement
• Carnot engine
• Carnot Refrigerator
• Sample Problems

24. Second Law of Thermodynamics:
Whenever energy is transferred, the level of
energy cannot be conserved and some
energy must be permanently reduced to a
lower level.
When this is combined with the first law of
thermodynamics, the law of energy conservation, the
statement becomes:
Whenever energy is transferred, energy
must be conserved, but the level of energy
cannot be conserved and some energy must
be permanently reduced to a lower level.

25. Kelvin-Planck statement of the Second Law:
No cyclic process is possible whose sole result
is the flow of heat from a single heat reservoir
and the performance of an equivalent amount
of work.
For a system undergoing a cycle:
The net heat is equal to the net work.
QW 
  dWdQ Where:
W - net work
Q - net heat

26. CARNOT CYCLE
Nicolas Leonard Sadi Carnot 1796-1832
1.Carnot Engine
Processes:
1 to 2 - Heat Addition (T = C)
2 to 3 - Expansion (S = C)
3 to 4 - Heat Rejection (T = C)
4 to 1 - Compression (S = C)
PV Diagram
TS Diagram

27. P
V
2
1
3
4
T = C
S = C
S = C
T = C

28. T
S
21
34
T H
T L
Q A
Q R

29. Heat Added (T = C)
QA = TH(S)  1
Heat Rejected (T = C)
QR = TL(S) 2
S = S2 - S1 = S3 – S4  3
Net Work
W = Q = QA - QR  4
W = (TH - TL)(S)  5
PV Diagram
TS Diagram

30. %x
Q
Q
e
%x
Q
QQ
e
%x
Q
W
e
A
R
A
RA
A
1001
100
100



  6
 7
 8
PV Diagram
TS Diagram

31. Substituting eq.1 and eq. 5 to eq 6
%x
T
T
e
%x
T
TT
e
H
L
H
LH
1001
100


  9
 10
PV Diagram
TS Diagram

32. TH
TL
W
QA
QR
E
Carnot Engine

33. 2. Carnot Refrigerator: Reversed
Carnot Cycle
Processes:
1 to 2 - Compression (S =C)
2 to 3 - Heat Rejection (T = C)
3 to 4 - Expansion (S = C)
4 to 1 - Heat Addition (T = C)
TS Diagram

34. QR
QA
1
2
4
3
S
T
TH
TL

35. Heat Added (T = C)
QA = TL(S)  1
Heat Rejected (T = C)
QR = TH(S) 2
S = S1 - S4 = S2 - S3  3
Net Work
W = Q 4
W = QR - QA  5
W = (TH - TL)(S)  6
TS Diagram

36. Coefficient of Performance
(COP)
LH
L
A
TT
T
COP
W
Q
COP


  7
 8
TS Diagram

37. Tons of Refrigeration
211 KJ/min = 1 TR
3. Carnot Heat Pump:A heat pump
uses the same components as the
refrigerator but its purpose is
to reject heat at high energy
level.

38. Performance Factor
(PF)
AR
R
R
QQ
Q
PF
W
Q
PF


  10
 11

39. 1
1
1





COPPF
T
T
PF
Q
Q
PF
TT
T
PF
L
H
A
R
LH
H
 12
 13
 14
 15

40. TH
TL
W
QA
QR
R
Carnot Refrigerator

41. A Carnot engine operating between 775 K and
305K produces 54 KJ of work. Determine the
change of entropy during heat addition.
TH = 775 K ; TL = 305 K
W = 54 KJ
TS Diagram

42. TH
TL
W
QA
QR
E

43. K
KJ
0.015
775
89.04
T
Q
S-S
)S-(STQ
KJ89.04
0.606
54
e
W
Q
Q
W
e
0.606
775
305775
T
TT
e
H
A
12
12HA
A
A
H
LH











44. A Carnot heat engine rejects 230 KJ of
heat at 25C. The net cycle work is 375 KJ.
Determine the cycle thermal efficiency and
the cycle high temperature .
Given:
QR = 230 KJ
TL = 25 + 273 = 298K
W = 375 KJ

45. TL = 298K
TH
WE
QR = 230 KJ
QA
K87.783
772.0
605
)S-(S
Q
T
KKJ/-0.772)S-(S
KKJ/772.0)SS(
)SS(298230
)SS(SS
)SS(TQ
)SS(TQ
62.0
605
375
QA
W
e
KJ605QA
)230375(QWQ
QQW
12
A
H
12
34
34
1234
34LR
12HA
RA
RA












46. A Carnot engine operates between temperature
reservoirs of 817C and 25C and rejects 25 KW to
the low temperature reservoir. The Carnot engine
drives the compressor of an ideal vapor compres-
sion refrigerator, which operates within pressure
limits of 190 KPa and 1200 Kpa. The refrigerant is
ammonia. Determine the COP and the refrigerant
flow rate.(4; 14.64 kg/min)
TH = 817 + 273 = 1090 K
TL = 25 + 273 = 298 K
QR = 25 KW