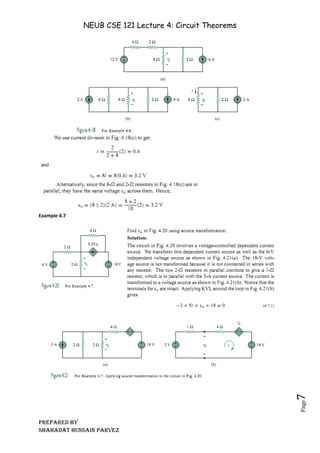
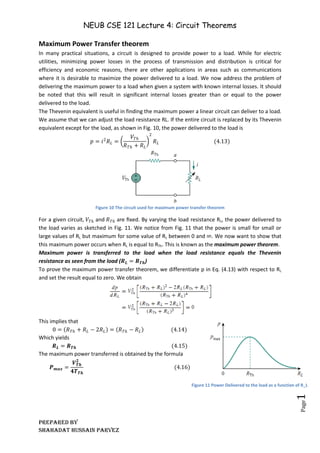
This lecture discusses circuit theorems, particularly Kirchhoff's laws, and introduces theorems like Thevenin's and Norton's to simplify circuit analysis of linear circuits. The concepts of superposition, source transformation, and maximum power transfer are also covered, explaining how circuit complexity can be managed without changing the circuit's configuration. Important properties such as linearity and techniques for calculating circuit equivalents are highlighted, making complex circuit analysis more manageable.