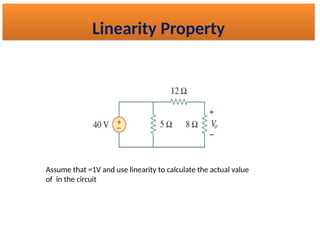
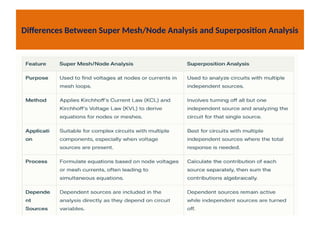
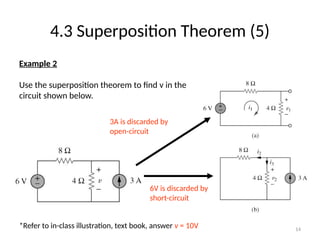
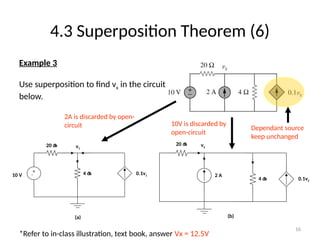
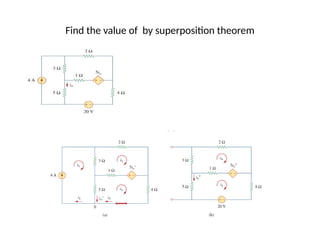
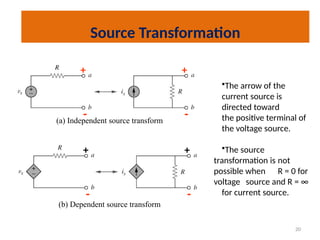
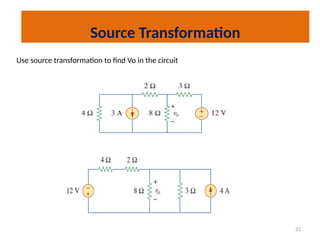
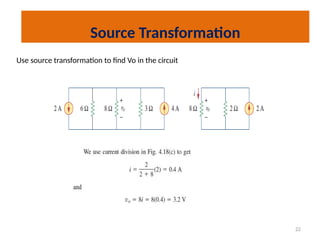
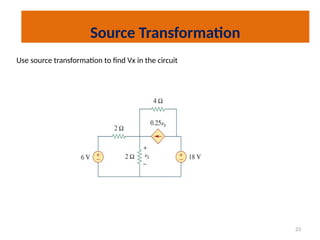
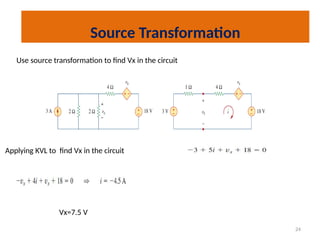
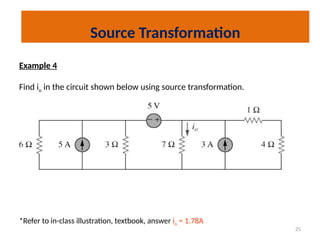
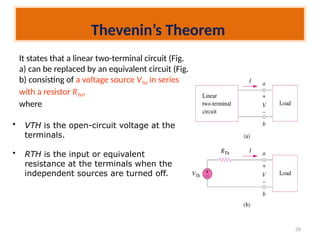
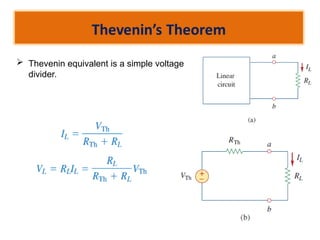
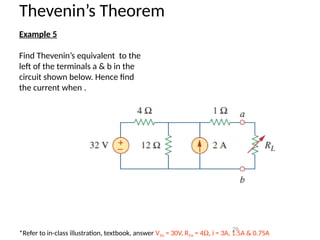
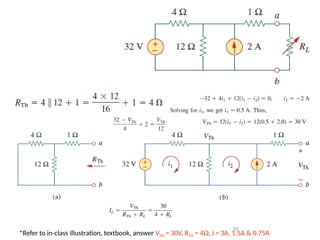
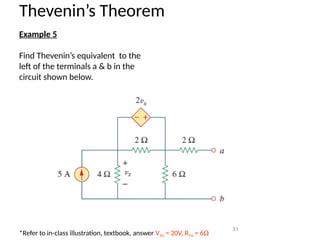
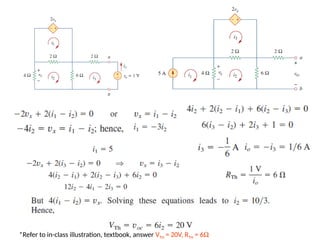
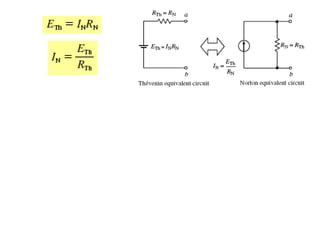
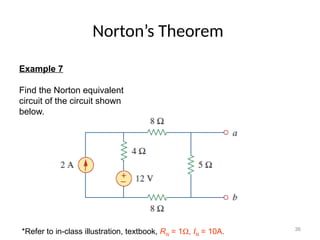
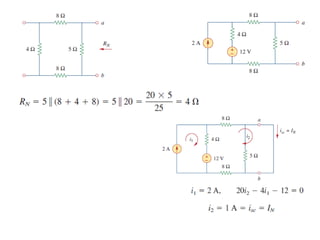
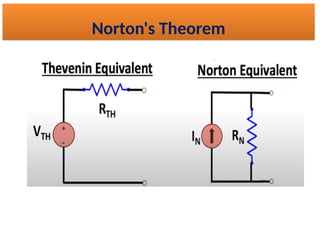
The document discusses various methods of linear circuit analysis, including linearity property, superposition, source transformation, Thevenin's theorem, and Norton's theorem. It explains key concepts such as the relationship between input and output in linear circuits, steps to apply superposition, and how to derive equivalent circuits using Thevenin and Norton methods. Examples illustrate the application of these principles to determine circuit parameters and contributions from independent sources.

2. By Lt Col Imran Nazir
Linear Circuit Analysis(LCA)
EE-111
Lecture-5

3. 3
Methods of Analysis
 Linearity Property
 Superposition
 Source Transformation
 Thevenin's Theorem
 Norton's Theorem
 Maximum Power Transfer

4. Linearity Property
 A linear Circuit is one whose output is linearly
related (or directly proportional ) to its input

5. 5
It is the property of an element describing a linear relationship
between cause and effect.
A linear circuit is one whose output is linearly related (or directly
proportional) to its input.
Homogeneity (scaling) property
v = i R → k v = k i R
Additive property
v1 = i1 R and v2 = i2 R
→ v = (i1 + i2) R = v1 + v2
Linearity Property

6. 6
Example 1
By assume Io = 1 A, use linearity to find the actual value of Io in the circuit shown
below.
*Refer to in-class illustration, text book, answer Io = 3A
Linearity Property

8. Assume that =1V and use linearity to calculate the actual value
of in the circuit
Linearity Property

9. 9
It states that the voltage across (or current through) an element
in a linear circuit is the algebraic sum of the voltage across (or
currents through) that element due to EACH independent
source acting alone.
The principle of superposition helps us to analyze a linear
circuit with more than one independent source by calculating
the contribution of each independent source separately.
Superposition Theorem

10. 11
4.3 Superposition Theorem (3)
Steps to apply superposition principle
1. Turn off all independent sources except one
source. Find the output (voltage or current)
due to that active source using nodal or
mesh analysis.
2. Repeat step 1 for each of the other independent
sources.
3. Find the total contribution by adding
algebraically all the contributions due to the
independent sources.

11. 12
Two things have to be keep in mind:
1. When we say turn off all other independent sources:
 Independent voltage sources are replaced by 0 V
(short circuit) and
 Independent current sources are replaced by 0 A
(open circuit).
2. Dependent sources are left intact because they are
controlled by circuit variables.

12. Differences Between Super Mesh/Node Analysis and Superposition Analysis

13. 14
4.3 Superposition Theorem (5)
Example 2
Use the superposition theorem to find v in the
circuit shown below.
3A is discarded by
open-circuit
6V is discarded by
short-circuit
*Refer to in-class illustration, text book, answer v = 10V

15. 16
4.3 Superposition Theorem (6)
Example 3
Use superposition to find vx in the circuit
below.
*Refer to in-class illustration, text book, answer Vx = 12.5V
2A is discarded by open-
circuit
20  v1
4 
10 V
+

(a)
0.1v1
4 
2 A
(b)
20 
0.1v2
v2
10V is discarded by
open-circuit
Dependant source
keep unchanged

16. Find the value of by superposition theorem

18. 19
Source Transformation
• An equivalent circuit is one whose v-i characteristics
are identical with the original circuit.
• It is the process of replacing a voltage source vS in
series with a resistor R by a current source iS in
parallel with a resistor R, or vice versa.

19. 20
(a) Independent source transform
(b) Dependent source transform
•The arrow of the
current source is
directed toward
the positive terminal of
the voltage source.
•The source
transformation is not
possible when R = 0 for
voltage source and R = ∞
for current source.
+
+
+
+
-
-
-
-
Source Transformation

20. 21
Source Transformation
Use source transformation to find Vo in the circuit

21. 22
Source Transformation
Use source transformation to find Vo in the circuit

22. 23
Source Transformation
Use source transformation to find Vx in the circuit

23. 24
Source Transformation
Use source transformation to find Vx in the circuit
Applying KVL to find Vx in the circuit
Vx=7.5 V

24. 25
Example 4
Find io in the circuit shown below using source transformation.
*Refer to in-class illustration, textbook, answer io = 1.78A
Source Transformation

25. 26
It states that a linear two-terminal circuit (Fig.
a) can be replaced by an equivalent circuit (Fig.
b) consisting of a voltage source VTH in series
with a resistor RTH,
where
• VTH is the open-circuit voltage at the
terminals.
• RTH is the input or equivalent
resistance at the terminals when the
independent sources are turned off.
Thevenin’s Theorem

26.  Thevenin equivalent is a simple voltage
divider.

27. Steps to converts any circuit into its Thévenin equivalent
1. Remove the load from the circuit.
2. Label the resulting two terminals.
3. Set all sources in the circuit to zero to determine the Thévenin equivalent
resistance, RTh, by calculating the resistance “seen” between terminals ‘a’ and
‘b’. It may be necessary to redraw the circuit to simplify this step
5. Replace the sources removed in Step 3, and determine the open-circuit voltage
between the terminals.
6. Draw the Thévenin equivalent circuit using the resistance
determined in Step 4 and the voltage calculated in Step 5.
7. As part of the resulting circuit, include that portion of the
network removed in Step 1

28. 29
Thevenin’s Theorem
Example 5
Find Thevenin’s equivalent to the
left of the terminals a & b in the
circuit shown below. Hence find
the current when .
*Refer to in-class illustration, textbook, answer VTH = 30V, RTH = 4W, i = 3A, 1.5A & 0.75A

29. 30
*Refer to in-class illustration, textbook, answer VTH = 30V, RTH = 4W, i = 3A, 1.5A & 0.75A

30. 31
Thevenin’s Theorem
Example 5
Find Thevenin’s equivalent to the
left of the terminals a & b in the
circuit shown below.
*Refer to in-class illustration, textbook, answer VTH = 20V, RTH = 6W

31. 32
*Refer to in-class illustration, textbook, answer VTH = 20V, RTH = 6W

32. 33
Norton’s Theorem
It states that a linear two-terminal circuit can be
replaced by an equivalent circuit of a current
source IN in parallel with a resistor RN,
Where
• IN is the short circuit current through
the terminals.
• RN is the input or equivalent resistance
at the terminals when the independent
sources are turned off.
The Thevenin’s and Norton equivalent circuits are related
by a source transformation.

34. Steps to convert cct in to Norten’s equivalent
1. Remove the load from the circuit.
2. Label the resulting two terminals. We will label them as a and b.
3. Set all sources to zero !
4. Determine the Norton equivalent resistance, RN. It may be necessary to
redraw the circuit to simplify this step.
5. Replace the sources removed in Step 3, and determine the current which
would occur in a short if the short were connected between terminals a
and b. If the original circuit has more than one source, it may be
necessary to use the Superposition Theorem.
6. Sketch the Norton equivalent circuit using the resistance determined in
Step 4 and the current calculated in Step 5. As part of the resulting
circuit, include that portion of the network removed in Step 1.

35. 36
Norton’s Theorem
Example 7
Find the Norton equivalent
circuit of the circuit shown
below.
*Refer to in-class illustration, textbook, RN = 1W, IN = 10A.

37. • Thevenin's Theorem states that any linear electrical network
can be reduced to an equivalent circuit consisting of a single
voltage source (Vth) in series with a resistor (Rth​
)
• This theorem is particularly useful for analyzing circuits with
multiple voltage sources and resistors by converting them into
a simpler form
Thevenin's Theorem

38. • Norton's Theorem, states that linear network can be
represented as an equivalent circuit consisting of a single
current source (In) in parallel with a resistor (Rn​
)
Norton's Theorem

39. Norton's Theorem

41. THANK YOU