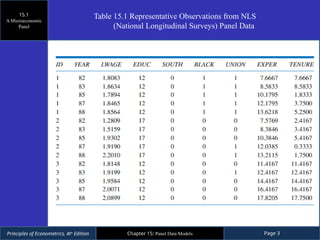
Chapter 15 of 'Principles of Econometrics' discusses panel data models, which integrate cross-sectional and time series data to analyze changes over time in multiple subjects. It differentiates between balanced and unbalanced panels and compares fixed effects and random effects models, highlighting the strengths and weaknesses of pooled least squares estimations and the implications of individual heterogeneity. The chapter also introduces the Hausman test for model selection between fixed and random effects models, providing guidance on when to use each model based on correlations between error components and explanatory variables.

1. Principles of Econometrics, 4th
Edition Page 1
Chapter 15: Panel Data Models
Chapter 4
Panel Data Models

2. Principles of Econometrics, 4th
Edition Page 2
Chapter 15: Panel Data Models
Panel data combines Cross-Sectional and Time
Series data and looks at multiple subjects and how
they change over the course of time.
Balanced and unbalanced panel
– In microeconomic panels, the individuals are not
always interviewed the same number of times, leading
to an unbalanced panel → In an unbalanced panel, the
number of time series observations is different across
individuals
– In a balanced panel, each individual has the same
number of observations
15.1
A Microeconomic
Panel Panel Data

3. Principles of Econometrics, 4th
Edition Page 3
Chapter 15: Panel Data Models
15.1
A Microeconomic
Panel
Table 15.1 Representative Observations from NLS
(National Longitudinal Surveys) Panel Data

4. Principles of Econometrics, 4th
Edition Page 4
Chapter 15: Panel Data Models
15.2
A Microeconomic Panel: Pooled
Least Squares Estimates

5. Principles of Econometrics, 4th
Edition Page 5
Chapter 15: Panel Data Models
A pooled least squares model is one where the
data on different individuals are simply pooled
together with no provision for individual
differences that may lead to different coefficients.
– Notice that the coefficients (β1, β2, β3) do not have i or t
subscripts
– The data for different individuals are pooled together,
and the equation is estimated using least squares
15.2
Pooled Model
1 2 2 3 3
it it it it
y x x e
   
Eq. 15.1

6. Principles of Econometrics, 4th
Edition Page 6
Chapter 15: Panel Data Models
What are the consequences of using pooled least
squares?
– The least squares estimator is consistent but its standard
errors are typically too small overstating the reliability
of the least squares estimator
– Unrealistic assumptions
• All individuals have the same coefficients
• The errors for different individuals are uncorrelated
15.2
Pooled Model
15.2.1
Cluster-Robust
Standard Errors

7. Principles of Econometrics, 4th
Edition Page 7
Chapter 15: Panel Data Models
15.3
The Fixed Effects Model

8. Principles of Econometrics, 4th
Edition Page 8
Chapter 15: Panel Data Models
We can extend the model in Eq. 15.1 to relax the
assumption that all individuals have the same
coefficients → Add an i subscript to the equation
A legitimate panel data model above (Eq. 15.7) is not
suitable for short (only 5 time-series observations)
and wide panels → Need a simplification
– The intercepts β1i are different for different individuals but
the slope coefficients β2 and β3 are assumed to be constant
for all individuals
15.3
The Fixed Effects
Model
Eq. 15.7
1 2 2 3 3
it i it it it
y x x e
   
Eq. 15.8

9. Principles of Econometrics, 4th
Edition Page 9
Chapter 15: Panel Data Models
All behavioral differences between individuals,
referred to as individual heterogeneity, are
captured by the intercept
– Individual intercepts are included to ‘‘control’’ for
individual-specific and time-invariant characteristics (i.e.,
gender, race and education)
– A model with these features is called a fixed effects
model
– The intercepts are called fixed effects
Fixed effects estimator is unable to estimate
coefficients on time-invariant variables like race and
gender.
15.3
The Fixed Effects
Model

10. Principles of Econometrics, 4th
Edition Page 10
Chapter 15: Panel Data Models
15.4
The Random Effects Model

11. Principles of Econometrics, 4th
Edition Page 11
Chapter 15: Panel Data Models
In the random effects model,
- we recognize that the individuals were randomly selected
- and thus we treat the individual differences as random
rather than fixed.
We can include random individual differences
- by specifying the intercept parameters to consist of a fixed
part that represents the population average
- and by specifying the random individual differences from
the population average:
The random individual differences ui are called
random effects (i.e., random individual effects or
random error terms)
15.4
The Random Effects
Model
1 1
i i
u
  

12. Principles of Econometrics, 4th
Edition Page 12
Chapter 15: Panel Data Models
15.5
Comparing Fixed and Random
Effects Estimators

13. Principles of Econometrics, 4th
Edition Page 13
Chapter 15: Panel Data Models
If random effects are present, then the random
effects estimator is preferred for several reasons:
1. The random effects estimator takes into account the
random sampling process by which the data were
obtained
2. The random effects estimator permits us to estimate
the effects of variables that are individually time-
invariant
3. The random effects estimator is a generalized least
squares estimation procedure, and the fixed effects
estimator is a least squares estimator  In large
samples, the GLS estimator has a smaller variance
than the LSE.
15.5
Comparing Fixed
and Random Effects
Estimators

14. Principles of Econometrics, 4th
Edition Page 14
Chapter 15: Panel Data Models
If the random error vit = ui + eit is correlated with
any of the right-hand-side explanatory variables in
a random effects model, then the GLS estimators
of the parameters are biased and inconsistent
– The problem is common in random effects models, because
the individual specific error component ui may well be
correlated with some of the explanatory variables
– A person’s ability and industriousness are variables not
explicitly included in the wage eq’n, and thus these factors
are included in ui. → These characteristics may be
correlated with his education level and/or job experiences →
RE estimator is inconsistent
15.5
Comparing Fixed
and Random Effects
Estimators
15.5.1
Endogeneity in the
Random Effects
Model

15. Principles of Econometrics, 4th
Edition Page 15
Chapter 15: Panel Data Models
To check for any correlation between the error
component ui (random individual effects) and the
regressors in a random effects model, we can use a
Hausman test
– The Hausman test can be carried out for specific
coefficients, using a t-test, or jointly, using an F-test or a chi-
square test
– The idea for the Hausman test is that both the random effects
and fixed effects estimators are consistent if there is no
correlation b/w error terms and the explanatory variables
– Null hypothesis of the Hausman test is that the difference
b/w the estimators is zero (two-tail test)  if reject the null,
then use the fixed effects estimator
15.5
Comparing Fixed
and Random Effects
Estimators
15.5.3
The Hausman Test

16. Principles of Econometrics, 4th
Edition Page 16
Chapter 15: Panel Data Models
Let the parameter of interest be βk
– Denote the fixed effects estimate as bFE,k and the
random effects estimate as bRE,k
– The t-statistic for testing that there is no difference
between the estimators is:
15.5
Comparing Fixed
and Random Effects
Estimators
15.5.3
The Hausman Test
 

 

   
, , , ,
1 2 1 2
2 2
, ,
, ,
se se
var var
FE k RE k FE k RE k
FE k RE k
FE k RE k
b b b b
t
b b
b b
 
 
   

  
   
 
Eq. 15.37

17. Principles of Econometrics, 4th
Edition Page 17
Chapter 15: Panel Data Models
Types of the Model for Panel Analysis
Pooled Least
Squares Estimation
Model Selection
– Hausman Test: FE and RE estimators are consistent (No
correlation between ui and the explanatory variables)
– Accept the null: FE=RE ⇒ Select the RE model
– Reject the null: FE≠RE ⇒ Select the FE model
Fixed Effects Model
(OLS)
Random Effects Model
(GLS)
• No individual heterogeneity=β1
•Uncorrelated errors
Random
Individual
Differences
Error terms are
correlated with
the explanatory
variables
15.5
Comparing Fixed
and Random
Effects Estimators