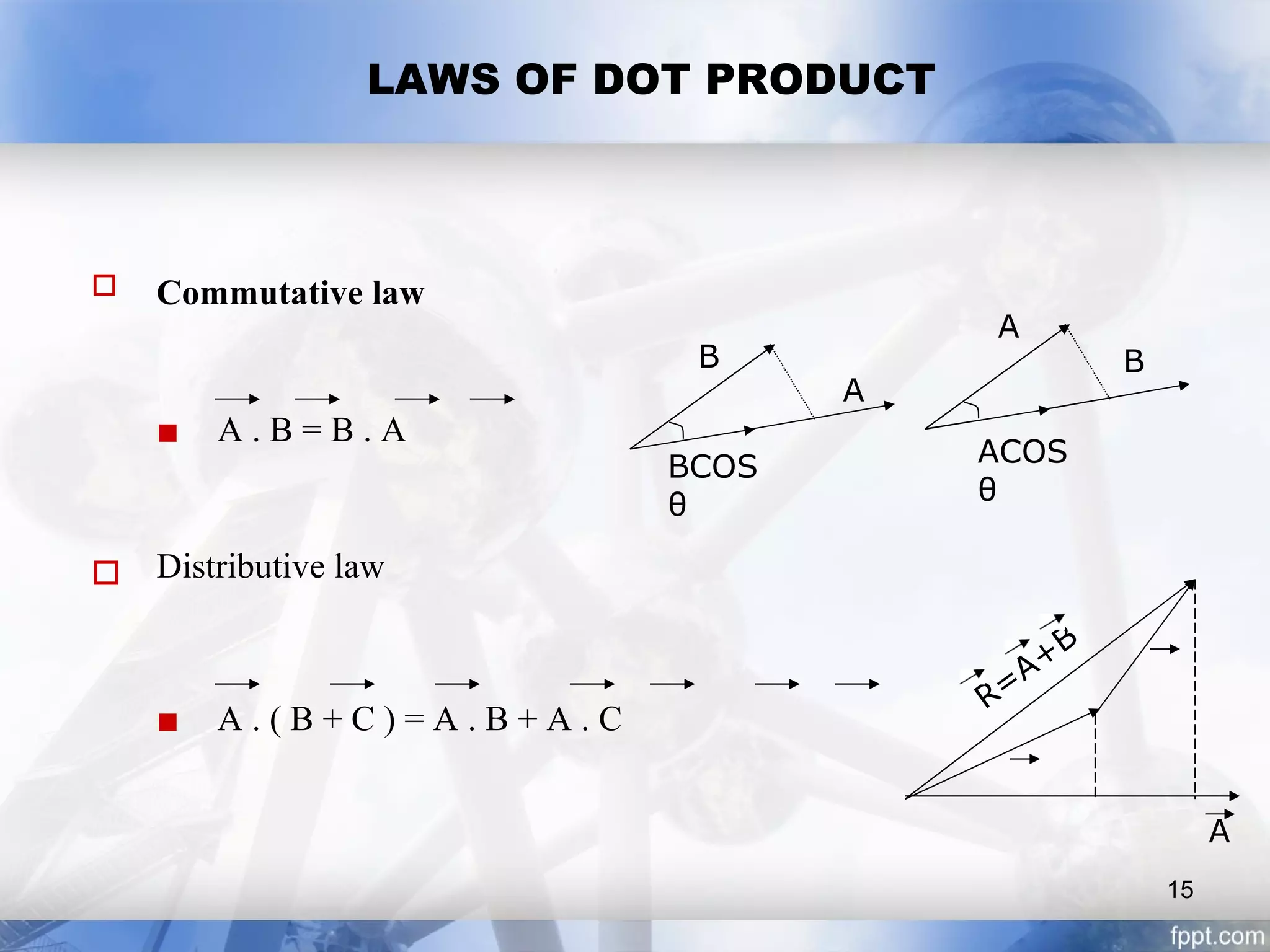
This presentation discusses vectors and their key properties. It begins by defining a vector as a quantity that has both magnitude and direction, and provides examples such as displacement, velocity, and acceleration. It then covers the importance of vectors in physics, the properties of vectors including their representation using arrows, and different types of vectors such as null and free vectors. The presentation also explains how to add and subtract vectors, resolve a vector into components, and calculate the scalar and cross products of vectors. It provides formulas for these operations and discusses their significance.

1. Presentation Title
VECTOR
1
INTERNATIONAL UNIVERSITY OF
BUSINESS AGRICULTURE
AND TECHNOLOGY (IUBAT)
COURSE NAME - PHY 109
SECTION - A

2. CONTENT
1. Introduction
2. Importance of vector
3. Properties of vector
4. Types of vector
5. Addition of vector
6. Subtraction of vectors
7. Resolution of a vector
8. Product of vectors
9. Scalar product
10. Scalar product in component from
11. Laws of dot product
12. What is cross product
13. Cross product
2

3. VECTOR
 Vector is a physical quantity which
have both magnitude and direction.
 Some examples are :
Displacement velocity
acceleration force momentum magnetic
density and
electric intensity.
3

4. WHY VECTORS ARE IMPORTANT
 Vectors are fundamental in the physical sciences. They can be used to
represent any quantity that has both a magnitude and direction, such
as velocity, the magnitude of which is speed.
4

5. PROPERTIES OF A VECTOR

A vector is a quantity that has
both direction and magnitude.
Let a vector be denoted by the


symbol A.
The magnitude of A is |A| ≡ A
We can represent vectors as
geometric objects using arrows.
The length of the arrow
corresponds to the magnitude of
the vector. The arrow points in
the direction of the vector
O
A
|A| ≡ A
5

6. TYPES OF VECTOR
 Null Vector

Vector with zero
magnitude Position Vector
Vector starting from
origin
Vector starting from anywhere but
origin

Free Vector

Unit Vector

Vector with magnitude of
1 Equal Vectors
 Two vectors equal in magnitude and
direction Opposite Vectors
 Two vectors equal in magnitude but opposite in
direction.
6

7. ADDITION OF VECTORS
 The addition of two vectors yields another vector known as Resultant
Vector.
 For example if vector A and vector B are added their sum will be equal to
(A+B).
7

8. SUBTRACTION OF VECTORS
 The subtraction of two
vectors can be treated as the
addition of a negative vector.
(P-Q)=P+(-Q)
 The vector (P-Q) can then be
determined by any of the two
methods.
P Q-
P
-Q
P-Q
P
-Q P-Q
=
OR
8

9. RESOLUTION OF A VECTOR
 Vector R could be considered to be the resultant of two vectors.
R=A+B
 Here the vectors A and B are known as the components of vectors.
9

10. RESOLUTION OF A VECTOR
It is useful to find the
components of a vector R in
two mutually perpendicular
directions. This process is
known as resolving a vector
into components.
The magnitude of the two
components can be written in
the form Rcos and Rsin
R
0
R

Rcos
Rsin
10

11. When vector is multiplied by another vector in some cases a scalar
quantity is obtained whereas in some other cases a vector quantity
obtained .There are two types of product.
Scalar product
Vector product
PRODUCT OF VECTORS
11

12. SCALAR PRODUCT
LENGTH/MAGNITUDE OF A VECTOR
The Dot Product of a vector with itself is always
equal to its magnitude squared
PARALLEL VECTORS
When A and B are parallel to each other,
their Dot Product is identical to the
ordinary multiplication of their sizes
PERPENDICULAR VECTORS
When A and B are perpendicular to each
other, their Dot Product is always Zero
12

13. SCALAR PRODUCT
 Since i and j and k are all one unit in length and they are all
mutually perpendicular, we have
i. i = j. j = k. k = 1
and i. j = j. i = i. k = k. i
= j. k = k. j = 0.
13

14. SCALAR PRODUCT IN COMPONENT FORM
Two vectors in component forms are written as
a=axi+ayj+azk b=bxi+byj+bzk
In evaluating the product, we make use of the fact that
multiplication of the same unit vectors is 1, while multiplication of
different unit vectors is zero. The dot product evaluates to scalar
terms as :
a.b=(axi+ayj+azk).(bxi+byj+bzk)
⇒a.b=axi.bxi+ayj.byj+azk.bzk
⇒a.b=axbx+ayby+azbz
14

15. LAWS OF DOT PRODUCT
 Commutative law
 A . B = B . A
 Distributive law
 A . ( B + C ) = A . B + A . C
B
BCOS
θ
A
B
ACOS
θ
A
A
R=A+B
15

16. WHAT IS CROSS PRODUCT
 In mathematics, the Cross Product is a binary operation on two vectors in thre
dimensional space that results in another vector which is perpendicular to the tw
input vectors.
 However the Dot Product produces a scalar result.
16

17. CROSS PRODUCT

 The cross product of two vectors a
and b is denoted by a × b.
The cross product is given by the formula :
 Where θ is the measure of the angle between a and b, a and b are
the magnitudes of vectors a and b, and is a unit vector
perpendicular to the plane containing a and b.
17

18. THE END
18