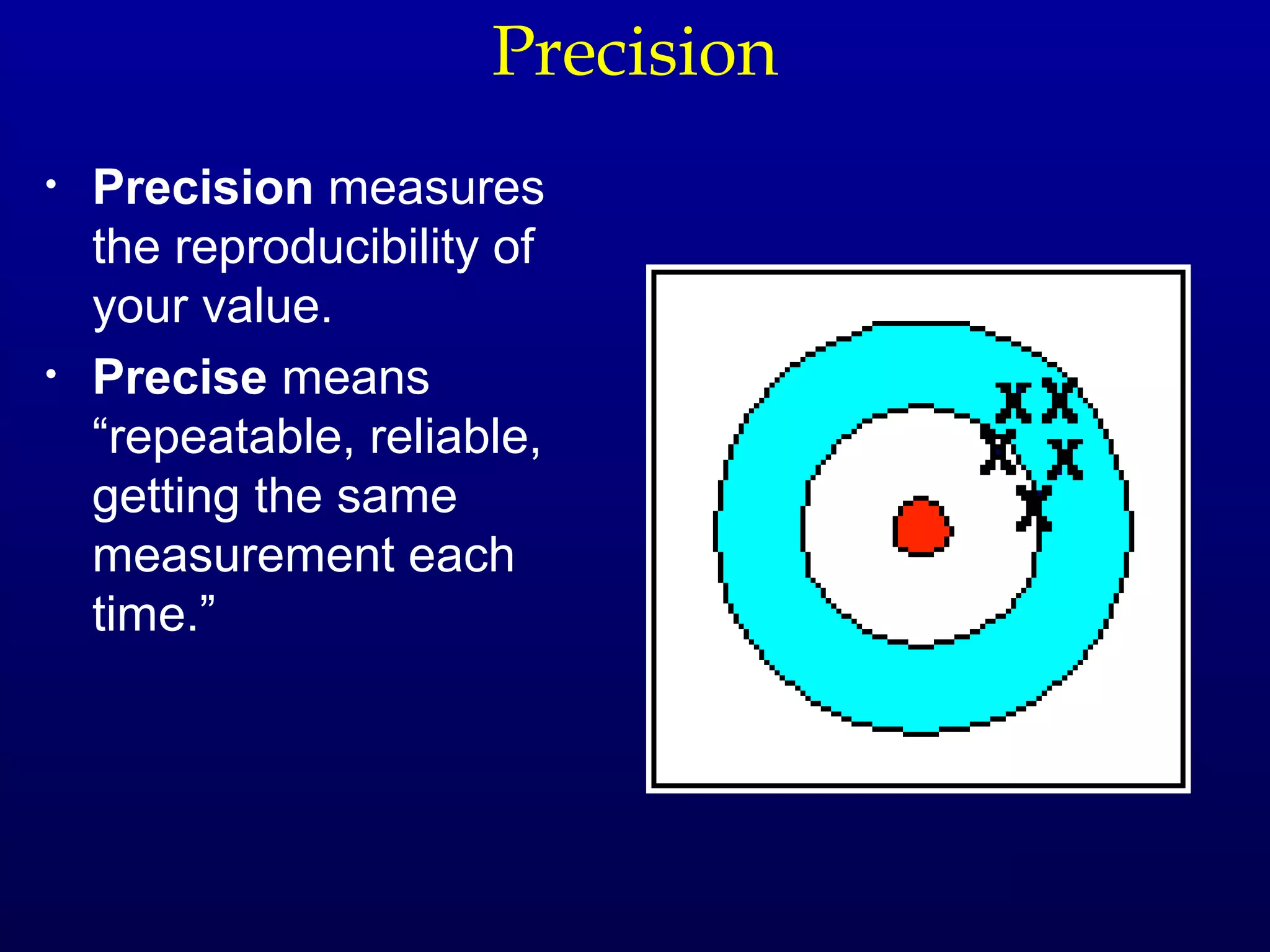
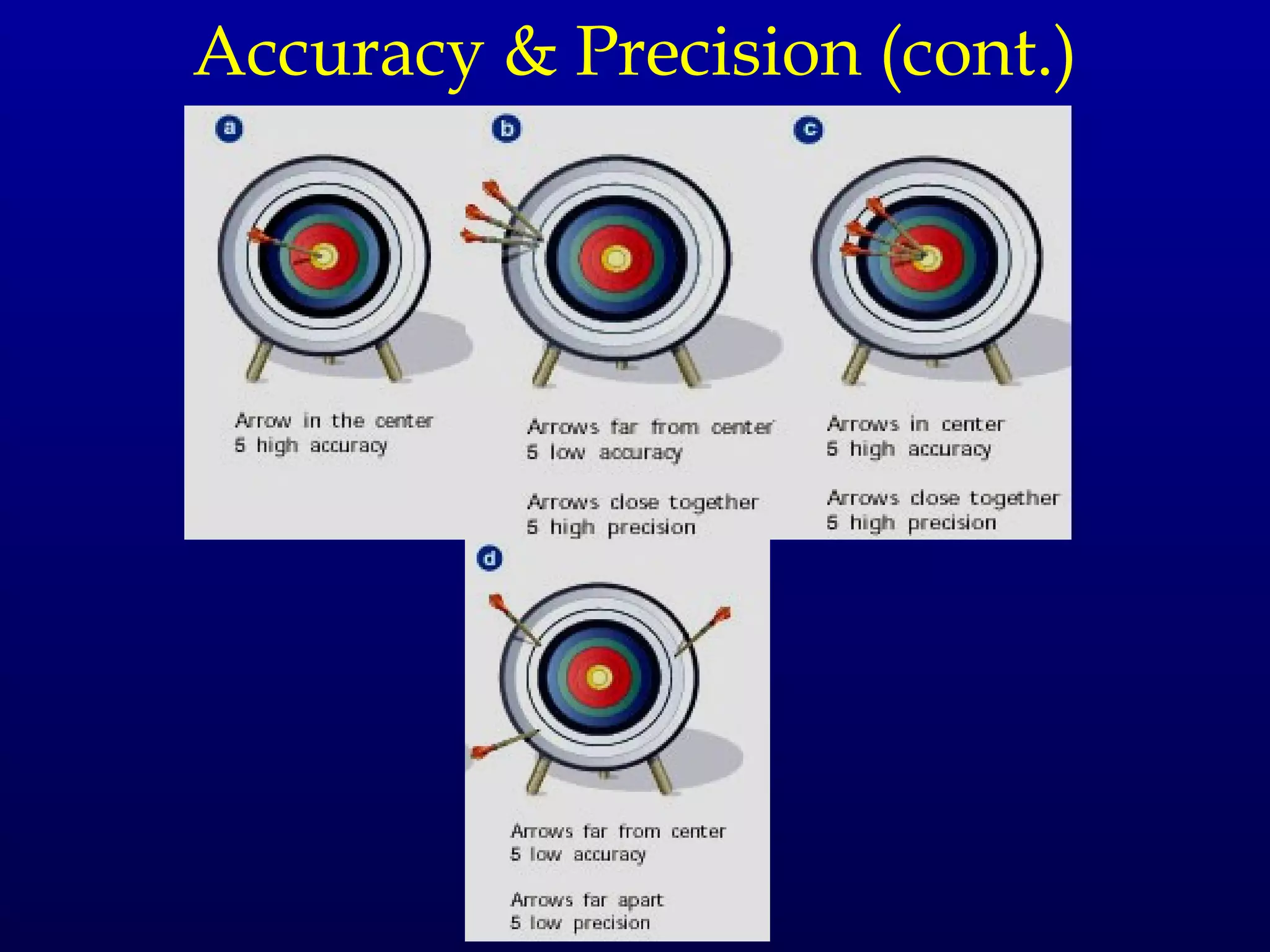
Here are the steps to write a number in standard form: 1. Locate the decimal point in the number. 2. Move the decimal point so that the number is greater than or equal to 1 but less than 10. 3. Count how many places the decimal was moved. If it was moved to the left, the exponent is positive. If it was moved to the right, the exponent is negative. 4. Write the number as the coefficient (the number with 1-9) and 10 with the exponent determined in step 3. For example: 0.00045 would be written as 4.5 × 10-4 Since the decimal was moved 3 places to the right,

1. Ch 100: Fundamentals for
Chemistry

2. What is Chemistry?
• Chemistry is considered to be the central science
• Chemistry is the study of matter
• Matter is the “stuff” that makes up the universe
• The fundamental questions of Chemistry are:
• How can matter be described?
• How does one type of matter interact with other types of
matter?
• How does matter transform into other forms of matter?

3. Types of Observations
• Qualitative
Descriptive/subjective in nature
Detail qualities such as color, taste, etc.
Example: “It is really warm outside today”
• Quantitative
Described by a number and a unit (an accepted
reference scale)
Also known as measurements
Example: “The temperature is 85oF outside
today”

4. Ch 100: Fundamentals for
Chemistry
Chapter 1: Measurements

5. UNITS OF MEASUREMENT
Measurements are quantitative information.
A measurement is more than just a number, even
in everyday life.
Suppose a chef were to write a recipe like
“1 salt, 3 sugar, 2 flour.”
The cooks could not use the recipe without more
information.
They need to know UNITS.

6. Quantities
• A measurement represents a quantity 
something that has size or amount
• Measurement and quantity NOT the same
• 1 liter  liter is unit of measurement, volume
is a quantity
• Almost every measurement requires a
number AND a unit

7. Measurements
• Described with a value (number) & a unit
(reference scale)
• Both the value and unit are of equal
importance!!
• The value indicates a measurement’s size
(based on its unit)
• The unit indicates a measurement’s
relationship to other physical quantities

8. Measurement Systems
There are 3 standard unit systems we will focus
on:
1. United States Customary System (USCS)
 formerly the British system of measurement
 Used in US, Albania, and a couple others
 Base units are defined but seem arbitrary (e.g. there are
12 inches in 1 foot)
2. Metric
 Used by most countries
 Developed in France during Napoleon’s reign
 Units are related by powers of 10 (e.g. there are 1000
meters in 1 kilometer)
3. SI (L’Systeme Internationale)
 a special set of metric units
 Used by scientists and most science textbooks
 Not always the most practical unit system for lab work

9. Related Units in the Metric System
• All units in the metric system are related to
the fundamental unit by a power of 10
• The power of 10 is indicated by a prefix
• The prefixes are always the same,
regardless of the fundamental unit

10. Metric Prefixes

11. Units & Measurement
• When a measurement has a specific unit (i.e.
25 cm) it can be expressed using different
units without changing its meaning
• Example:
» 25 cm is the same as 0.25 m or even 250 mm
• The choice of unit is somewhat arbitrary,
what is important is the observation it
represents

12. Basic Quantities and SI Units
1. SI units
2. Base and derived quantities
3. Prefixes

13. S.I. UNITS
• Le system International d’unites
• A modification of the older French
metric system.

14. Base Units
Base units are considered so
because they are not derived
from any pre-existing number or
formula. We need to be able to
discuss things like distance,
temperature and time, and we
do so by agreeing to a reliable
definition of some basic (base!)
facts.

15. THE BASE QUANTITIES & UNITS
QUANTITY UNIT SYMBOL
mass kilogram kg
length metre m
time second s
electric current ampere (amp) A
thermodynamic kelvin K
temperature
amount of mole mol
substance
luminous intensity candela cd

16. EXAMPLES OF DERIVED UNITS
QUANTITY UNIT DERIVED
UNIT
frequency hertz (Hz) s-1
speed m s-1 m s-1
acceleration m s-2 m s-2
force newton (N) kg m s-2
energy joule (J) kg m2 s-2
power watt (W) kg m2 s-3
electric charge coulomb (C) As
potential difference volt (V) kg m2 s-3 A-1
electrical resistance ohm (Ω) kg m2 s-3 A-2
specific latent heat J kg-1 K-1 m2 s-2 K-1

17. The more commonly used prefixes
peta P 1015
tera T 1012
giga G 109
mega M 106
kilo k 103
deci d 10-1
centi c 10-2
milli m 10-3
micro μ 10-6
nano n 10-9
pico p 10-12
femto f 10-15
atto a 10-18

18. Mass and Weight
Mass: the measure of the quantity or amount of
matter in an object. The mass of an object does not
change as Its position changes.
Weight: A measure of the gravitational attraction of
the earth for an object. The weight of an object
changes with its distance from the center of the earth.
Sample Calculations Involving Masses
How many mg are in 2.56 kg?
(2.56 kg)(103 g)(103mg)
= 2.56 x 106 mg
(1 kg) ( 1 g)

19. Volume
• The units for volume are given by (units of length)3.
i.e., SI unit for volume is 1 m3.
• A more common volume unit is the liter (L)
1 L = 1 dm3 = 1000 cm3 = 1000 mL.
• We usually use 1 mL = 1 cm3.
Sample Calculations Involving Volumes
How many mL are in 3.456 L?
(3.456 L)(1000 mL) = 3456 mL
L
How many ML are in 23.7 cm3?
(23.7 cm3)( 1 mL )( 1 L_ _)(106 ML)
(1 cm3)(1000 mL)( 1L )
= 23 700 ML = 2.37 x 10 4 ML

20. Density
Density - The mass of a unit volume of a material.
density = mass/volume
What is the density of a cubic block of wood that is
2.4 cm on each side and has a mass of 9.57 g?
volume = [2.4 cm x 2.4 cm x 2.4 cm]
density = (9.57 g)/(13.8 cm3)
= 0.69 g/cm3 = 0.69 g/mL
Note that 1 cm3 = 1 mL

21. Temperature
21

22. Temperature
Conversions:
K = oC + 273.15
273 K = 0 oC
373 K = 100 oC
o
C = 5 (oF – 32)
9
o
F = 9 (oC) + 32
5
32 oF = 0 oC
212 oF = 100 oC

23. Temperature
Kelvin Scale
Used in science.
Same temperature increment as Celsius scale.
Lowest temperature possible (absolute zero) is zero Kelvin.
Absolute zero: 0 K = -273.15oC.
Celsius Scale
Also used in science.
Water freezes at 0oC and boils at 100oC.
To convert: K = oC + 273.15.
Fahrenheit Scale
Not generally used in science.
Water freezes at 32oF and boils at 212oF.
Converting between Celsius and Fahrenheit
5 9
° = (° - 32 )
C F ° = (° ) +32
F C
9 5

24. Sample Calculations Involving Temperatures
Convert 73.6oF to Celsius and Kelvin temperatures.
o
C = (5/9)(oF - 32) K = oC + 273.15
Memorize
o
C = (5/9)(73.6oF - 32) = (5/9)(41.6) = 23.1oC
K = 23.1oC + 273.15 = 296.3 K

25. Measurement & Uncertainty
• A measurement always has some
amount of uncertainty
• Uncertainty comes from limitations of
the techniques used for comparison
• To understand how reliable a
measurement is, we need to
understand the limitations of the
measurement

26. Exact numbers vs. Measured numbers
 Exact numbers are numbers that are defined
 Infinite number of significant figures present in
exact numbers
 Zero uncertainty
 Measured numbers are an estimated amount –
dependent on the measuring tool
 Limited number of significant figures present in
measured numbers
 Always some uncertainty in the measurement

27. Significant Figures
• Significant figures are used to distinguish truly
measured values from those simply resulting from
calculation.
• Significant figures determine the precision of a
measurement.
• Precision refers to the degree of subdivision of a
measurement.

28. Significant Figures
• Significant figures in a measurement are of
all the digits known with certainty plus one
final digit, which is somewhat uncertain or is
estimated

29. Why do significant figures matter?
 Show how precisely the data has been
measured
 Greater number of significant figures means
the measuring tool is more precise
 Incorrectly adding more significant figures
makes it seem that you have more precision
than truly exists
 Not having enough significant figures makes it
seem that you have less precision than the
measuring tools provided
What do significant figures not
tell us?
• If a measurement is truly accurate

31. Rules for Counting Significant Figures
• Nonzero integers are always significant
• Exact numbers have an unlimited number of
significant figures
• Zeros ….. The problem

32. Rules for Determining Significant Zeros
Rule Examples
1. Zeros appearing between nonzero digits a. 40.7 L has three sig figs
are significant. b. 87,009 km has five sig figs
2. Zeros appearing in front of all nonzero a. 0.095897 m has five sig figs
digits are NOT significant. b. 0.0009 kg has one sig fig
3. Zeros at the end of a number and to the a. 85.00 g has four sig figs
right of a decimal point are significant. b. 9.000000000 mm has ten sig figs
4. Zeros at the end of a number but to the a. 2000 m may contain from one to four
left of a decimal point may or may not be sig figs, depending on how many zeros
significant. If a zero has not been are placeholders. For measurements
measured or estimated but is just a given in this text, assume that 2000 m
placeholder, it is not significant. A decimal has one sig fig.
point placed after zeros indicates they are b. 2000. m contains four sig figs, indicated
significant. by the presence of the decimal point

33. No decimal
point
2 sig figs Zeros are not
significant!
Decimal
Point
All digits including
zeros to the left of
The decimal are
significant.
6 sig figs

34. All figures are
Significant
4 sig figs
Zeros between
Non zeros are
significant
All figures are
Significant
5 sig figs
Zero to the
Right of the
Decimal are
significant

35. 3 sig figs
Zeros to the right of
The decimal with no
Non zero values
Before the decimal
Are not significant
5 sig figs
Zeros to the right of the decimal
And to the right of non zero values
Are significant

36. Sample Problem
How many significant figures are in each of the
following measurements?
a. 28.6 g
three
b. 3440. cm
four
c. 910 m
two
d. 0.046 04 L
four
e. 0.006 700 0 kg
five

37. Practice Problems
1. Determine the number of significant figures in
each of the following.

38. Measurements & Significant Figures
• To indicate the uncertainty of a single
measurement scientists use a system
called significant figures
• The last digit written in a measurement
is the number that is considered to be
uncertain
• Unless stated otherwise, the uncertainty
in the last digit is ±1

39. Scientific Notation
• Technique Used to Express Very Large or
Very Small Numbers
• Based on Powers of 10
• To Compare Numbers Written in Scientific
Notation
First Compare Exponents of 10 (order of
magnitude)
Then Compare Numbers

40. Scientific Notation
• In scientific notation, numbers are written
in the form M x 10n, where the factor M is a
number greater than or equal to 1 but less
than 10 and n is a whole number.
• Ex. 65,000 km in scientific notation is
• 6.5 x 104 km

41. Scientific numbers use powers of 10

42. RULE 1
As the decimal is moved to the left Any number to the
The power of 10 increases one Zero power = 1
value for each decimal place moved

43. RULE 2
As the decimal is moved to the right Any number to the
The power of 10 decreases one Zero power = 1
value for each decimal place moved

44. RULE 3
When scientific numbers are multiplied
The powers of 10 are added

45. RULE 4
When scientific numbers are divided
The powers of 10 are subtracted

46. RULE 5
When scientific numbers are raised to powers
The powers of 10 are multiplied

47. RULE 6
Roots of scientific numbers are treated as fractional
powers. The powers of 10 are multiplied

48. RULE 7
When scientific numbers are added or subtracted
The powers of 10 must be the same for each term.
Powers of 10 are
Different. Values
Cannot be added !
Move the decimal
And change the power
Of 10
Power are now the
Same and values
Can be added.

49. Writing Numbers in Scientific Notation
1 Locate the Decimal Point
2 Move the decimal point to the right of the
non-zero digit in the largest place
 The new number is now between 1 and 10
3 Multiply the new number by 10n
 where n is the number of places you moved the
decimal point
4 Determine the sign on the exponent, n
 If the decimal point was moved left, n is +
 If the decimal point was moved right, n is –
 If the decimal point was not moved, n is 0

50. Example
• 0.000 12 mm = 1.2 × 10−4 mm
• Move the decimal point four places to the right
and multiply the number by 10−4
• 1. Determine M by moving the decimal point in
the original number to the left or the right so that
only one nonzero digit remains to the left of the
decimal point.
• 2. Determine n by counting the number of places
that you moved the decimal point. If you moved it
to the left, n is positive. If you moved it to the
right, n is negative.

51. Writing Numbers in Standard Form
1 Determine the sign of n of 10n
If n is + the decimal point will move to the right
If n is – the decimal point will move to the left
2 Determine the value of the exponent of 10
Tells the number of places to move the decimal
point
3 Move the decimal point and rewrite the
number

52. Rules for Rounding Off
• If the digit to be removed
• is less than 5, the preceding digit stays the same
• is equal to or greater than 5, the preceding digit
is increased by 1
• In a series of calculations, carry the extra
digits to the final result and then round off
• Don’t forget to add place-holding zeros if
necessary to keep value the same!!

53. Addition or Subtraction
• When adding or subtracting decimals, the
answer must have the same number of digits
to the right of the decimal point as there are
in the measurement having the fewest digits
to the right of the decimal point.
25.1 g + 2.03 g = 27.13 g
27.1 g

54. The numbers in
these positions are
not zeros, they are
unknown
The sum of an
unknown number
and a 6 is not valid.
The same is true
The answer is rounded to the
For the 2
position of least significance

55. Multiplication and Division
• For multiplication and division, the answer
can have no more significant figures than are
in the measurement with the fewest number
of significant figures.
= 0.360094451 g/mL
= 0.360 g/mL

56. Uncertainty,
Precision & Accuracy
in Measurements

57. Definitions Accuracy and
Precision …sound
the same thing…
…is there a
difference??

58. ACCURACY
MEANS HOW CLOSE A MEASUREMENT
IS TO THE TRUE VALUE
PRECISION
REFERS TO THE DEGREE OF
SUBBDIVISION OF THE MEASUREMENT

60. Accuracy
• Accuracy is the extent to
which a measurement
approaches the true
value.
• Accurate means
"capable of providing a
correct reading or
measurement." A
measurement is accurate
if it correctly reflects the
size of the thing being
measured.

61. Precision
• Precision measures
the reproducibility of
your value.
• Precise means
“repeatable, reliable,
getting the same
measurement each
time.”

62. Accuracy & Precision
• Accuracy is how close to the accepted value.
• Precision is how close a series of
measurements are to each other.

63. Accuracy & Precision (cont.)

64. Accuracy & Precision (cont.)
• Students collected density data for powered
sucrose.
• The accepted density is 1.59 g/cm 3.
Density Data Collected by Three different
Students
Student A Student B Student C
Trial 1 1.54 g/cm3 1.40 g/cm3 1.70 g/cm3
Trial 2 1.60 g/cm3 1.68 g/cm3 1.69 g/cm3
Trial 3 1.57 g/cm3 1.45 g/cm3 1.71 g/cm3
Average 1.57 g/cm3 1.51 g/cm3 1.70 g/cm3

65. 1-5 Summary
• What is the difference between accuracy and
precision?

66. Precision and Accuracy
Accuracy – how close a measurement is to the true or
accepted value
To determine if a measured value is accurate, you would
have to know what the true or accepted value for that
measurement is – this is rarely known!
Precision – how close a set of measurements are to
each other; the scatter of repeated measurements
about an average.
We may not be able to say if a measured value is accurate,
but we can make careful measurements and use good
equipment to obtain good precision, or reproducibility.

67. Precision and Accuracy
A target analogy is often used to compare accuracy and
precision.
accurate precise not accurate
& but &
precise not accurate not precise