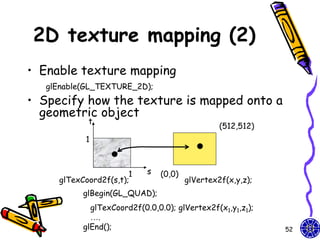
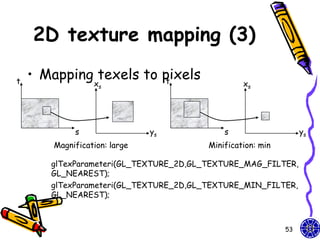
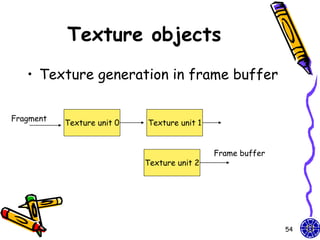
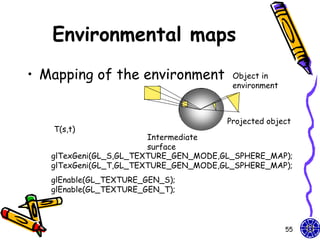
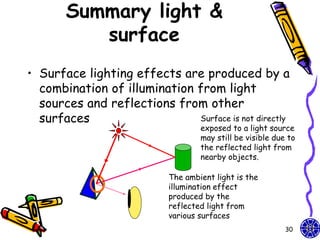
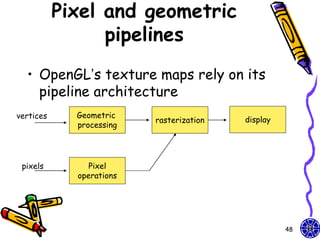
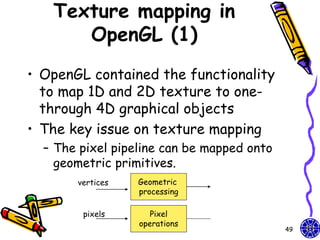
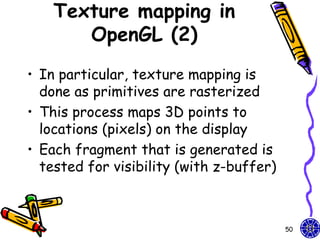
The document discusses various techniques for constructing shadows and lighting effects in 3D computer graphics, including using projection matrices to generate shadow polygons and accounting for factors like light source positioning, radial intensity attenuation, and surface reflectance properties. It also examines methods for animating camera movement and introducing texture mapping to surfaces.

1. Shadows + Light
+Texture
Chen Jing-Fung (2006/12/15)
Assistant Research Fellow,
Digital Media Center,
National Taiwan Normal University
Ch10: Computer Graphics with OpenGL 3th, Hearn Baker
Ch6: Interactive Computer Graphics 3th, Addison Wesley
Ch7: Interactive Computer Graphics 3th, Addison Wesley

2. outline
• How to construct the object’s
shadow in a scene
• Camera’s walking in a scene
• Several kinds about light
2

3. shadows
• Create simple shadows is an
interesting application of projection
matrices
– Shadows are not geometric objects in
OpenGL
– Shadows can realistic images and give
many visual clues to the spatial
relationships among objects in a scene
3

4. How to create the
object’s shadow
• Starting from a view point
• Lighting source is also required
(infinitely light)
– If light source is at the center of
projection, there are no visible shadows
(shadows are behind the objects)
4

5. Polygon’s shadow
y
• Consider the shadow (xl,yl,zl)
generated by the point source
– Assume the shadow falls on the
surface (y=0)
x
– Then, the shadow polygon is z
related to original polygon
• Shadow ~ origin
5

6. y
(xl,yl,zl)
z x
• Find a suitable projection matrix and use
OpenGL to compute the vertices of the
shadow polygon
is projected to
– (x,y,z) in space -> (xp, yp, zp) in
projection plane
– Characteristic:
• All projectors pass through the origin and all
projected polygon through the vertical to y-axis
6

7. y
(xl,yl,zl)
z x
• Shadow point and polygon point are
projected from x-axis to y-axis
x (xp,-d)
(x,y) xp x x
 xp 
d y y / d
y yp = -d
• Project from z-axis to y-axis
(zp,-d) z
(z,y) zp z z
 zp 
d y y / d
y y = -d
p
7

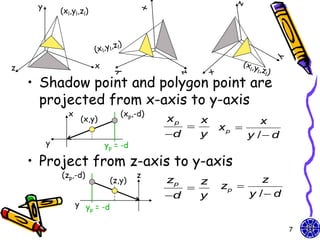
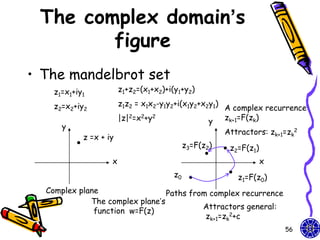
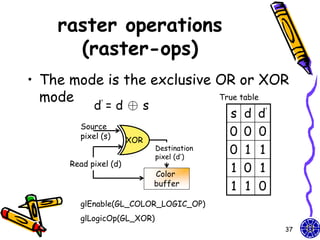
8. Homogeneous
coordinates
• Original homogeneous coordinates:
x  x p  1 0 0 0  x 
xp 
y / d  y  0 1 0 0  y 
 p    
yp = y  zp  0 0 1 0  z 
zp 
z   0 1 
0 0  1 
y / d 1   d  
Perspective projection matrix: Our light can be
shadow projection Matrix moved by design
GLfloat light[3]={0.0, 10.0, 0.0};
GLfloat m[16]; light[0]=10.0*sin((6.28/180.0)*theta);
light[2]=10.0*cos((6.28/180.0)*theta);
for(i=0;i<16;i++) m[i]=0.0;
m[0]=m[5]=m[10]=1.0; m[7]=-1.0/light[1];
8

9. Orthogonal view with
clipping box
glClear(GL_COLOR_BUFFER_BIT|GL_DEPTH_BUFFER_BIT);
/* set up standard orthogonal view with clipping */
/* box as cube of side 2 centered at origin */
glMatrixMode (GL_PROJECTION);
glLoadIdentity ();
glOrtho(-2.0, 2.0, -2.0, 2.0, -5.0, 5.0);
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
gluLookAt(1.0,1.0,1.0,0.0,0.0,0.0,0.0,1.0,0.0);
// view plane up vector at y-axis (0.0,1.0,0.0)
9

10. Polygon & its shadow
/* define unit square polygon */
glColor3f(1.0, 0.0, 0.0);/* set drawing/fill color to red*/
glBegin(GL_POLYGON);
glVertex3f(…); …
glEnd();
glPushMatrix(); //save state
glTranslatef(light[0], light[1],light[2]); //translate back
glMultMatrixf(m); //project
glTranslatef(-light[0], -light[1],-light[2]); //return origin
//shadow object
glColor3f(0.0,0.0,0.0);
glBegin(GL_POLYGON);
glVertex3f(…);…
glEnd();
glPopMatrix(); //restore state
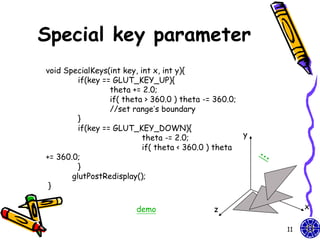
How to design the different size
between original polygon & its shadow?
10

11. Special key parameter
void SpecialKeys(int key, int x, int y){
if(key == GLUT_KEY_UP){
theta += 2.0;
if( theta > 360.0 ) theta -= 360.0;
//set range’s boundary
}
if(key == GLUT_KEY_DOWN){
theta -= 2.0; y
if( theta < 360.0 ) theta
+= 360.0;
}
glutPostRedisplay();
}
demo z x
11

12. How to design walking
object?
• Walking direction?
• Viewer (camera) parameter
• Reshape projected function
12

13. Viewer (camera) moving (1)
• Viewer move the camera in a scene by
depressing the x, X, y, Y, z, Z keys on
keyboard
void keys(unsigned char key, int x, int y){
if(key == ‘x’) viewer[0] -= 1.0;
if(key == ‘X’) viewer[0] += 1.0;
if(key == ‘y’) viewer[1] -= 1.0;
if(key == ‘Y’) viewer[1] += 1.0;
if(key == ‘z’) viewer[2] -= 1.0;
if(key == ‘Z’) viewer[2] += 1.0;
glutPostRedisplay(); }
Walking in a scene.
What problem happen if object is walked far away?
13

14. Viewer (camera) moving (2)
• The gluLookAt function provides a
simple way to reposition and reorient
the camera
void display(void){
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glLoadIdentity();
gluLookAt(viewer[0],viewer[1],viewer[2],0.0,0.0,0.0,0.0,1.0,0.0);
/* rotate cube */
glRotatef(theta[0], 1.0, 0.0, 0.0);
glRotatef(theta[1], 0.0, 1.0, 0.0);
glRotatef(theta[2], 0.0, 0.0, 1.0);
colorcube();
glFlush();
glutSwapBuffers(); }
14

15. Viewer (camera) moving (3)
• Invoke glFrustum in the reshape
callback to specify the camera lens
void myReshape(int w, int h){
glViewport(0, 0, w, h);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
if(w<=h) glFrustum(-2.0, 2.0, -2.0 * (GLfloat) h/ (GLfloat) w,
2.0* (GLfloat) h / (GLfloat) w, 2.0, 20.0);
else glFrustum(-2.0, 2.0, -2.0 * (GLfloat) w/ (GLfloat) h,
2.0* (GLfloat) w / (GLfloat) h, 2.0, 20.0);
glMatrixMode(GL_MODELVIEW); }
demo
15

16. Light & surface
• Light reflection method is very
complicated
– Describe that light source is reflected from an
actual surface
– Maybe depends an many factors
• Light source’s direction, observer’s eye and the
normal to the surface
– Surface characteristics can also consider that its
roughness or surface’s color … (surface’s texture)
16

17. Why do shading?
• Set a sphere model to cyan
– Result
• the sphere seem like a circle
• We want to see a sphere
– Material + light + viewer + surface
orientation
• The material’s color can be designed
to a gradual transformation
17

18. Lighting phenomenon
• Light sources
– Point light sources
• Infinitely distant light sources
• Radial intensity attenuation
– Directional light sources and spotlight
effects
• Angular intensity attenuation
• Surface lighting effects
18

19. Point light sources
• The simplest model for an object and
its light source
– Light rays are generated along radially
diverging paths from the single-color
source position
• light source is a single color
– The light source’s size is smaller than object
– We can use an illumination model to calculate the
light direction to a selected object surface’s
position
19

20. Infinitely distant light
sources
• A large light source (sun) that is very far
from a scene like a point light source
• Large light source is small different to
point light source
– When remote the point light source, the
object is illuminated at only one direction
– In constant to sun which is very far so it
shines everywhere
20

21. Radial intensity
attenuation (1)
• As radiant energy from a light source
travels outwards through space, its
amplitude at any distance dl from the
source is decreased by the factor
1/dl2 d ’
l
Energy =1 light
Energylight = 1/dl’ 2
dl
Energylight = 1/dl2
21

22. Radial intensity
attenuation (2)
• General form to the object about the
infinity light source and point light
source
 1.0 if source is at infinity

fl ,radatten  1
 a0  a1d l  a2d l

2 if source is local
22

23. Directional light sources
and spotlight effects
• A local light source can easily be modified
to produce a directional, or spotlight,
beam of light.
– The unit light-direction vector defines the axis
of a light cone, the angle θl defines the angular
extent of the circular cone
Vlight
Light direction
vector
Light
source θl
23

24. spotlight effects
• Denote Vlight in the light-source direction
and Vobj in the direction from the light
position to an object position
To object Vobj
vertex
α Cone axis Vlight
vector if Vobj .Vlight < cosθl
->
Light Vobj .Vlight = cos α the object is outside
source the light cone
cos α >= cosθl
θl
00 <θl<= 900
24

25. Angular intensity
attenuation
• For a directional light source, we can
degrade the light intensity angularly
about the source as well as radially
out from the point-source position.
– Light intensity decreasing as we move
farther from the cone axis
– Common angular intensity-attenuation
function for a directional light source
f angatten( )  cos al  0    
25

26. Attenuation function
f angatten( )  cos al  0    
– al (attentuation exponent) is assigned
positive value
• (al: the greater value in this function)
– Angle φis measured from the cone axis
• Along the cone axis, φ=0o fangatten(φ)=1.0
26

27. Combination above
different light sources
• To determine the angular attenuation
factor along a line from the light
position to a surface position in a
scene
 1.0 if source is not a spotlight

f l ,radatten   0.0 if Vobj .Vlight = cos α < cosθl
(V  V ) al
 obj light otherwise
27

28. Surface lighting effects
• Besides light source can light to
object, object also can reflect lights
– Surfaces that are rough so tend to
scatter the reflected light
• when object exist more faces of surface,
more directions can be directed by the
reflected light
28

29. Specular reflection
• Some of the reflected light is
concentrated into a highlight called
specular reflection
– The lighting effect is more outstanding
on shiny surfaces
29

30. Summary light &
surface
• Surface lighting effects are produced by a
combination of illumination from light
sources and reflections from other
surfaces Surface is not directly
exposed to a light source
may still be visible due to
the reflected light from
nearby objects.
The ambient light is the
illumination effect
produced by the
reflected light from
various surfaces
30

31. Homework
• Walking in a scene
void polygon(int a, int b, int c , int d){
– Hint: Object glBegin(GL_POLYGON);
walking or walking glColor3fv(colors[a]);
glNormal3fv(normals[a]);
above floor glVertex3fv(vertices[a]);
glColor3fv(colors[b]);
– Example: color glNormal3fv(normals[b]);
cube glVertex3fv(vertices[b]);
glColor3fv(colors[c]);
glNormal3fv(normals[c]);
glVertex3fv(vertices[c]);
glColor3fv(colors[d]);
glNormal3fv(normals[d]);
glVertex3fv(vertices[d]);
glEnd(); }
demo
31

32. Texture
Ch10: Computer Graphics with OpenGL 3th, Hearn Baker
Ch7: Interactive Computer Graphics 3th, Addison Wesley

33. Mapping methods
• Texture mapping
• Environmental maps
• The complex domain’s figure
33

34. Simple buffer mapping
• How we design program which can both
write into and read from buffers.
• (Generally, two factors make these operations
different between reading and writing into computer
memory)
– First, read or write a single pixel or bit
– Rather, extend to read and write rectangular
blocks of pixels (called bit blocks)
34

35. Example: read &
write
I love
monitor OpenGL
• Our program would follow user controlling
when user assign to fill polygon, user key
some words or user clear the window
• Therefore, both the hardware and
software support a set of operations
– The set of operations work on rectangular
blocks of pixels
• This procedure is called bit-block transfer
• These operations are raster operations (raster-ops)
35

36. bit-block transfer
(bitblt)
• Take an n*m block from the source
buffer and to copy it into another
buffer (destination buffer)
Write_block(source,n,m,x,y,destination,u,v);
• source and destination are the buffer
• the n*m source block which lower-left
corner is at (x,y) to the destination
destination
buffer at a location (u,v)
• the bitblt is that a single function call
alters the destination block source
n Frame buffer
m
36

37. raster operations
(raster-ops)
• The mode is the exclusive OR or XOR
mode True table
’ d=d⊕s
s d d’
Source
pixel (s) 0 0 0
XOR
Destination
pixel (d’)
0 1 1
Read pixel (d)
Color
1 0 1
buffer
1 1 0
glEnable(GL_COLOR_LOGIC_OP)
glLogicOp(GL_XOR)
37

38. Erasable Line
• What is Erasable Line ?
• How to implement?
38

39. Drawing erasable lines
• Why line can erasable
– Line color and background color are combined togrther
• How to do
– First, we use the mouse to get the first endpoint and
store it.
xm=x/500.; ym=(500-y)/500.;
– Then, get the second point and draw a line segment in
XOR mode
xmm = x/500.; ymm=(500-y)/500.;
glColor3f(1.0,0.0,0.0);
glLogicOp(GL_XOR);
glBegin(GL_LINES);
glVertex2f(xm,ym);
glVertex2f(xmm,ymm);
glEnd();
glLogicOp(GL_COPY);
glFlush();
39

40. Texture mapping
• Texture mapping which describe a
pattern map to a surface
• describe texture: parametric
compute
textures
Regular pattern
40
Ch7: Interactive Computer Graphics 3th, Addison Wesley

41. Texture elements
• Texture elements which can be put in
a array T(s,t)
– This array is used to show a continuous
rectangular 2D texture pattern
– Texture coordinates (s, t) which are
independent variables
• With no loss of generality, scale (s, t) to the
interval (0, 1)
41

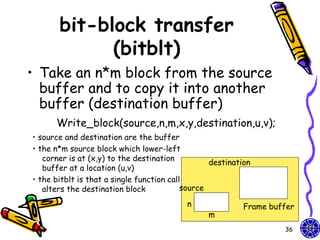
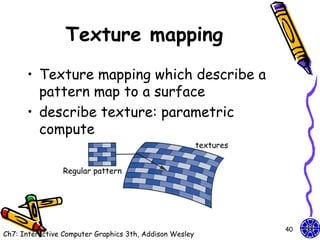
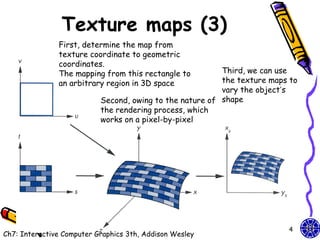
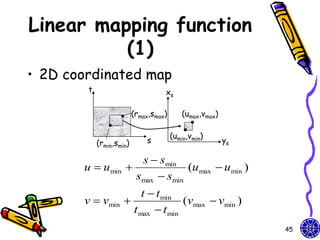
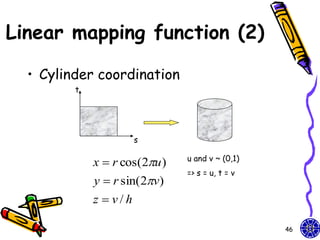
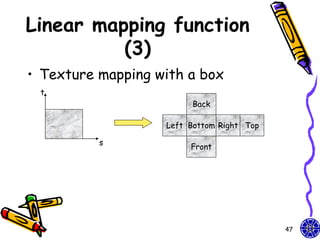
42. Texture maps (1)
• Texture map on a geometric object where
mapped to screen coordinates for display
– Object in spatial coordinates [(x,y,z) or
(x,y,z,w)] & texture elements (s,t)
• The mapping function:
x = x(s,t), y = y(s,t), z = z(s,t), w = w(s,t)
• The inverse function:
s = s(x,y,z,w), t = t(x,y,z,w)
42

43. Texture maps (2)
• If the geometric object in (u,v)
surface (Ex: sphere…)
– Object’s coordination (x,y,z) - > (u,v)
– Parametric coordinates (u,v) can also be
mapped to texture coordinates
– Consider the projection process from
worldcoordination to screencoordination
• xs = xs(s,t), ys = ys(s,t)
43

44. Texture maps (3)
First, determine the map from
texture coordinate to geometric
coordinates.
The mapping from this rectangle to Third, we can use
an arbitrary region in 3D space the texture maps to
vary the object’s
Second, owing to the nature of shape
the rendering process, which
works on a pixel-by-pixel
44
Ch7: Interactive Computer Graphics 3th, Addison Wesley

45. Linear mapping function
(1)
• 2D coordinated map
t xs
(rmax,smax) (umax,vmax)
(umin,vmin)
(rmin,smin) s ys
s  smin
u  umin  (umax  umin )
smax  smin
t  t min
v  vmin  (vmax  vmin )
t max  t min
45

46. Linear mapping function (2)
• Cylinder coordination
t
s
u and v ~ (0,1)
x  r cos(2u )
=> s = u, t = v
y  r sin( 2v)
z  v/h
46

47. Linear mapping function
(3)
• Texture mapping with a box
t
Back
Left Bottom Right Top
s
Front
47

48. Pixel and geometric
pipelines
• OpenGL’s texture maps rely on its
pipeline architecture
vertices Geometric
rasterization display
processing
pixels Pixel
operations
48

49. Texture mapping in
OpenGL (1)
• OpenGL contained the functionality
to map 1D and 2D texture to one-
through 4D graphical objects
• The key issue on texture mapping
– The pixel pipeline can be mapped onto
geometric primitives.
vertices Geometric
processing
pixels Pixel
operations
49

50. Texture mapping in
OpenGL (2)
• In particular, texture mapping is
done as primitives are rasterized
• This process maps 3D points to
locations (pixels) on the display
• Each fragment that is generated is
tested for visibility (with z-buffer)
50

51. 2D texture mapping (1)
• Support we have a 512*512 image my_texels
GLubye my_texels[512][512]
• Specify this array is too be used as a 2D texture
glTexImage2D(GL_TEXTURE_2D, level, components,
width, height, border, format,type,tarry);
– tarray size is the same the width*height
– The value components is the (1-4) of color components
(RGBA) or 3 (RGB)
– The format (RGBA) = 4 or 3 (RGB)
– In processor memory, tarry’s pixels are moved through
the pixel pipeline (** not in the frame buffer)
– The parameters level and border give us fine control
Ex: glTexImage2D(GL_TEXTURE_2D, 0, 3, 512, 512,
0, GL_RGB,GL_UNSIGNED_BYTE,my_texels);
51

52. 2D texture mapping (2)
• Enable texture mapping
glEnable(GL_TEXTURE_2D);
• Specify how the texture is mapped onto a
geometric object
t
(512,512)
1
1 s (0,0)
glTexCoord2f(s,t); glVertex2f(x,y,z);
glBegin(GL_QUAD);
glTexCoord2f(0.0,0.0); glVertex2f(x1,y1,z1);
….
glEnd(); 52

53. 2D texture mapping (3)
t
• Mapping texels to pixels
t
xs xs
s ys s ys
Magnification: large Minification: min
glTexParameteri(GL_TEXTURE_2D,GL_TEXTURE_MAG_FILTER,
GL_NEAREST);
glTexParameteri(GL_TEXTURE_2D,GL_TEXTURE_MIN_FILTER,
GL_NEAREST);
53

54. Texture objects
• Texture generation in frame buffer
Fragment
Texture unit 0 Texture unit 1
Frame buffer
Texture unit 2
54

55. Environmental maps
• Mapping of the environment Object in
environment
Projected object
T(s,t)
Intermediate
surface
glTexGeni(GL_S,GL_TEXTURE_GEN_MODE,GL_SPHERE_MAP);
glTexGeni(GL_T,GL_TEXTURE_GEN_MODE,GL_SPHERE_MAP);
glEnable(GL_TEXTURE_GEN_S);
glEnable(GL_TEXTURE_GEN_T);
55

56. The complex domain’s
figure
• The mandelbrot set
z1=x1+iy1 z1+z2=(x1+x2)+i(y1+y2)
z2=x2+iy2 z1z2 = x1x2-y1y2+i(x1y2+x2y1)
A complex recurrence
|z|2=x2+y2 y zk+1=F(zk)
y
Attractors: zk+1=zk2
z =x + iy
z3=F(z2) z2=F(z1)
x x
z0 z1=F(z0)
Complex plane Paths from complex recurrence
The complex plane’s
Attractors general:
function w=F(z)
zk+1=zk2+c
56

57. Pixels & display
The area centered at
-0.75+i0.0
If |zk|>4, break
0~255 -> Rarray
demo
57