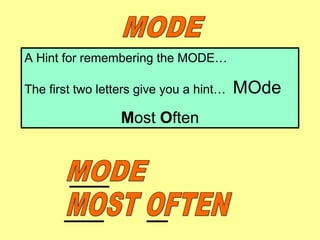
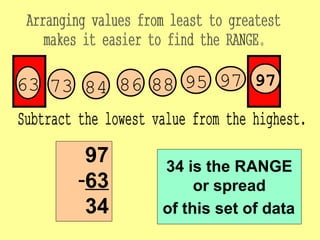
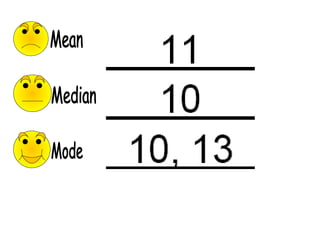
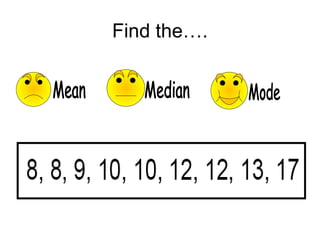
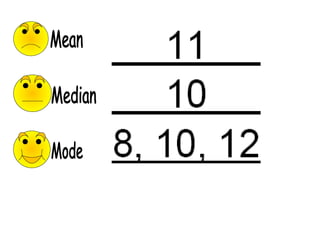
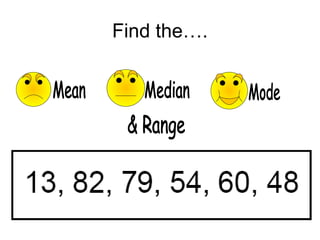
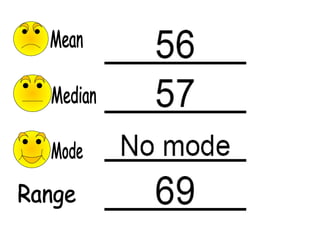
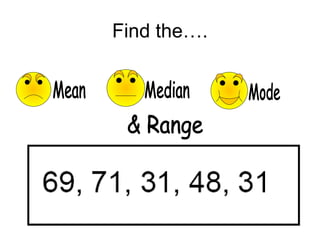
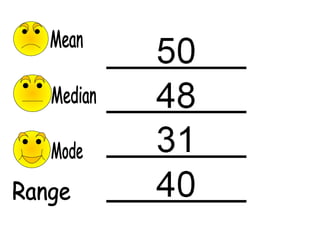
The document provides information about calculating the mean, median, mode, range, variance, and standard deviation of a data set of test scores for nine vocational technical students. It gives the definitions and step-by-step processes for finding each measure. As an example, it calculates the mean as 87, the median as 88, the mode as 97, and the range as 34 for the data set of test scores {63, 73, 84, 86, 88, 95, 97, 97, 100}. It then works through calculating the variance as 135.1 and the standard deviation as 11.6 for this same data set.

2. These are Voc Tech Students test
scores.
97 84
73 88
100
63
97 95
86

3. What can you tell us about these
numbers?
97 84
73 88
100
63
97
95
86

5. What is the MEAN?
How do we find it?
The mean is the numerical average
of the data set.
The mean is found by adding all the
values in the set, then dividing the
sum by the number of values.

6. Lets find Students
of Voc Tech MEAN
test score?
97
84
73
88
100
63
97
95
86
+
783
783 ÷ 9
The mean is 87

7. What is the MEDIAN?
How do we find it?
The MEDIAN is the number that is in the
middle of a set of data
1. Arrange the numbers in the set in
order from least to greatest.
2. Then find the number that is in the
middle.

8. 978473 88 10063 979586
The median is 88.
Half the numbers are
less than the median.
Half the numbers are
greater than the median.

9. Median
Sounds like
MEDIUM
Think middle when you hear median.

10. How do we find
the MEDIAN
when two numbers are in the middle?
1. Add the two numbers.
2. Then divide by 2.

11. 978473 88 10063 9795
88 + 95 = 183
183 ÷ 2 The median is
91.5

12. What is the MODE?
How do we find it?
The MODE is the piece of data that
occurs most frequently in the data set.
A set of data can have:
• One mode
• More than one mode
• No mode

13. 978473 88 10063 979586
The value 97 appears twice.
All other numbers appear just once.
97 is the MODE

14. A Hint for remembering the MODE…
The first two letters give you a hint… MOde
Most Often

15. What is the RANGE?
How do we find it?
The RANGE is the difference between the
lowest and highest values.

16. 978473 8863 979586
97
-63
34
34 is the RANGE
or spread
of this set of data

17. This one is the requires more
work than the others.
Right in the
MIDDLE.
This one is the easiest to
find— Just LOOK.

18. Find the….

20. Find the….

22. Find the….

24. Find the….

26. Variance and
Standard Deviation

27. • Variance is the average squared
deviation from the mean of a set of
data. It is used to find the standard
deviation.
Variance

28. 1. Find the mean of the data.
Hint – mean is the average so add up the
values and divide by the number of items.
2. Subtract the mean from each value – the
result is called the deviation from the mean.
3. Square each deviation of the mean.
4. Find the sum of the squares.
5. Divide the total by the number of items.
6.Take the square root of the variance – result is
the standard deviation.

29. Variance Formula
• The variance formula includes
the Sigma Notation, , which
represents ∑ the sum of all
the items to the right
of Sigma.
∑(x−µ)2
n
Mean is represented by and µ n
is the number of items.

30. Standard Deviation
• Standard Deviation shows the variation
in data. If the data is close together, the
standard deviation will be small. If the data
is spread out, the standard deviation will
be large.
• Standard Deviation is often denoted
by the lowercase Greek letter σ
sigma, .

31. Standard Deviation
• Find the variance.
• Find the mean of the data.
• Subtract the mean from each value.
• Square each deviation of the mean.
• Find the sum of the squares.
• Divide the total by the number of items.
• Take the square root of the variance.

32. Standard Deviation Formula
• Notice the standard deviation formula is
the square root of the variance.
The standard deviation formula can be represented
using
Sigma Notation:
σ=
∑(x−µ)2
n

33. 2. Find the variance and
standard deviation
• The test scores of nine voctech students
are: 63,73,84,86,88,95,97,97,100
1. Find the mean:
(63,73,84,86,88,95,97,97,100)and /9=87.

34. Find the deviation from the
mean:
63-87=-24 97-87=10
73-87=-14 97-87=10
84-87=-3 100-87=13
86-87=-1
88-87=1
95-87=8

35. 3. Square the deviation from
the mean:

36. 4. Find the sum of the squares
of the deviation from the mean:
576+196+9+1+1+64+100+100+169= 1216

37. 5. Divide by the number of data
items to find the variance:
1216
9
= 135.1 -
135.1

38. 6. ) Find the square root of the
variance:
135.1 = 11.6
Thus the standard deviation of the test
scores is 11.6

39. Thank you
very much muwah