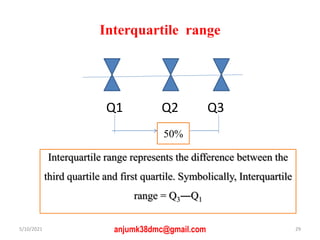
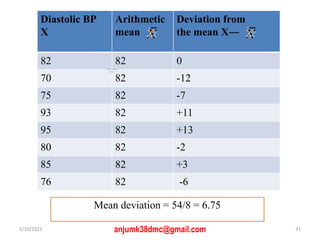
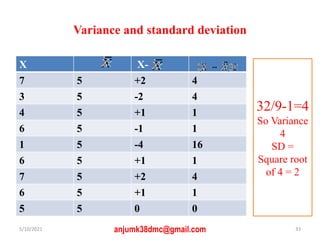
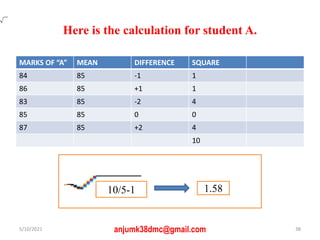
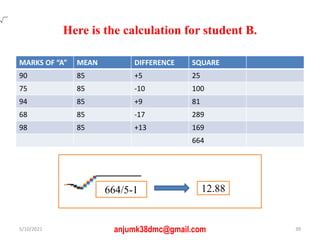
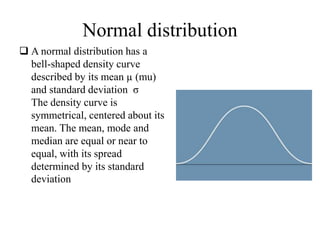
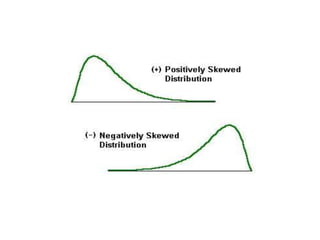
The document discusses central tendency and measures of dispersion in statistics. It covers mean, median, and mode as measures of central tendency, detailing their definitions, advantages, and disadvantages, as well as calculations necessary to determine them. It also addresses measures of dispersion, including range, variance, and standard deviation, highlighting their significance in understanding data distributions.