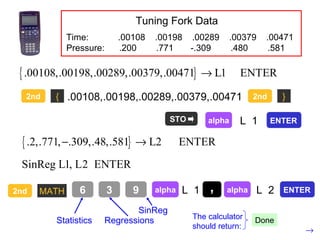
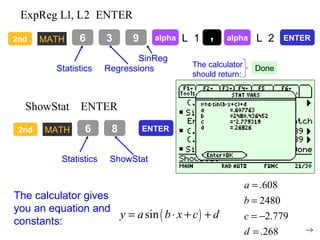
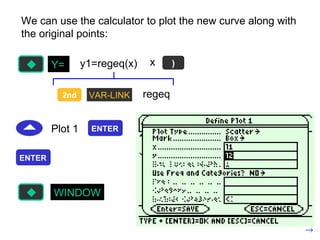
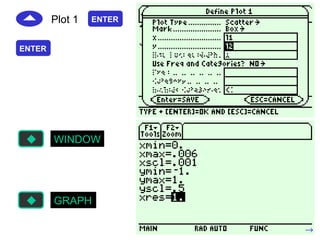
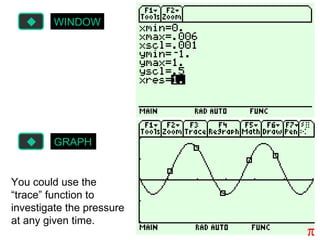
Trigonometric functions are used extensively in calculus. When using trig functions in calculus, radian measure must be used for angles. Even trig functions like cosine are symmetric about the y-axis, while odd functions like sine change sign when x changes sign. Trig functions can be shifted, stretched, or shrunk by applying transformations to their graphs.

1. Trig Functions By Kairui Zeng

2. Trigonometric functions are used extensively in calculus. If you want to brush up on trig functions, they are graphed in your book. When you use trig functions in calculus, you must use radian measure for the angles. The best plan is to set the calculator mode to radians and use when you need to use degrees. 2nd o

3. Even and Odd Trig Functions: “ Even” functions behave like polynomials with even exponents, in that when you change the sign of x , the y value doesn’t change. Secant is also an even function, because it is the reciprocal of cosine. Even functions are symmetric about the y - axis. Cosine is an even function because:

4. Even and Odd Trig Functions: “ Odd” functions behave like polynomials with odd exponents, in that when you change the sign of x , the sign of the y value also changes. Cosecant, tangent and cotangent are also odd, because their formulas contain the sine function. Odd functions have origin symmetry. Sine is an odd function because:

5. The rules for shifting, stretching, shrinking, and reflecting the graph of a function apply to trigonometric functions. Vertical stretch or shrink; reflection about x -axis Horizontal stretch or shrink; reflection about y -axis Horizontal shift Vertical shift Positive c moves left . Positive d moves up . The horizontal changes happen in the opposite direction to what you might expect. is a stretch . is a shrink .

6. When we apply these rules to sine and cosine, we use some different terms. Horizontal shift Vertical shift is the amplitude . is the period . A B C D

7. Trig functions are not one-to-one. However, the domain can be restricted for trig functions to make them one-to-one. These restricted trig functions have inverses. Inverse trig functions and their restricted domains and ranges are defined in the book. 

8. The sine equation is built into the TI-89 as a sinusoidal regression equation . For practice, we will find the sinusoidal equation for the tuning fork data in the book. To save time, we will use only five points instead of all the data.

9. Time: .00108 .00198 .00289 .00379 .00471 Pressure: .200 .771 -.309 .480 .581 2nd { .00108,.00198,.00289,.00379,.00471 2nd } alpha L 1 2nd MATH 6 3 Statistics Regressions 9 SinReg alpha L 1 alpha L 2 Done The calculator should return: , Tuning Fork Data STO ENTER ENTER

10. 2nd MATH 6 8 Statistics ShowStat The calculator gives you an equation and constants: 2nd MATH 6 3 Statistics Regressions 9 SinReg alpha L 1 alpha L 2 Done The calculator should return: , ENTER ENTER

11. We can use the calculator to plot the new curve along with the original points: y1=regeq(x) 2nd VAR-LINK regeq x ) Plot 1 Y= ENTER ENTER WINDOW

12. Plot 1 ENTER ENTER WINDOW GRAPH

13. You could use the “trace” function to investigate the pressure at any given time.  WINDOW GRAPH