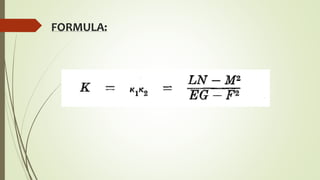This document provides information on different types of curvatures in differential geometry including normal, principal, mean, Gaussian, and geodesic curvatures. It defines each type of curvature, provides examples and formulas. Normal curvature is the amount of curve bending in the direction of the surface normal. Principal curvatures are the maximum and minimum normal curvatures. Mean curvature is the average of the principal curvatures. Gaussian curvature is the product of the principal curvatures. Geodesic curvature measures how far a curve is from being the shortest path between points on a surface.

2. COMPLEX ANALYSIS
PRESENTED TO : MA’AM HUNZA
PRESENTED BY : AMENAH GONDAL
CLASS: BS.ED (VI)

3. NORMAL , PRINCIPAL , MEAN
, GUASSIAN , GEODESIC
CURVATURES

4. CURVATURE:
 In differential geometry, curvature is the rate of
change of direction of a curve at a point on that
curve, or the rate of change of inclination of the
tangent to a certain curve relative to the length of
arc.

5. NORMAL CURVATURE:
“The normal curvature at a point is the amount of the
curve's curvature in the direction of the surface normal. The
curve on the surface passes through a point , with
tangent, curvature and normal.”

6. EXAMPLES:

7. FORMULA:
 Kn is the function of the surface parameters L, M, N,
E, F, G and of the direction du/dt.

8. EXAMPLE:

9. PRINCIPAL CURVATURE:
“The maximum and minimum of the normal curvature
k1 and k2 at a given point on a surface are called
the principal curvatures. The principal curvatures measure
the maximum and minimum bending of a regular surface at
each point.”
FORMULA:
A number k is a principal curvature iff k is a solution of
the equation

10. MEAN CURVATURE:
(
1
)
Let K1 and K2 be the principal curvatures, then their mean
is called the mean curvature.
Let and be the radii corresponding to the principal
curvatures, then the multiplicative inverse of the mean
curvature is given by the multiplicative inverse of
the harmonic mean,
=

11. GUASSIAN CURVATURE:
“The Gaussian curvature or Gauss curvature Κ of a
surface at a point is the product of the principal
curvatures, κ₁ and κ₂, at the given point.”
For example, a sphere of radius r has Gaussian
curvature everywhere, and a flat plane and a cylinder
have Gaussian curvature zero everywhere.

12. FORMULA:

14. GEODESIC CURVATURE:
GEODESIC:
 In differential geometry, a geodesic is a curve
representing in some sense the shortest path between
two points in a surface.
GEODESCI CURVATURE:
The geodesic curvature of a curve measures how
far the curve is from being a geodesic.

15. The curvature vector at P of the projection of the curve
C onto the tangent at P is called the Geodesic Curvature
Vector of C at P is denoted by Kg.

16. FORMULA:
kg = kgU
The scalar kg is called the geodesic curvature of C at P.