Embed presentation
Download to read offline

![Physics Helpline
L K Satapathy
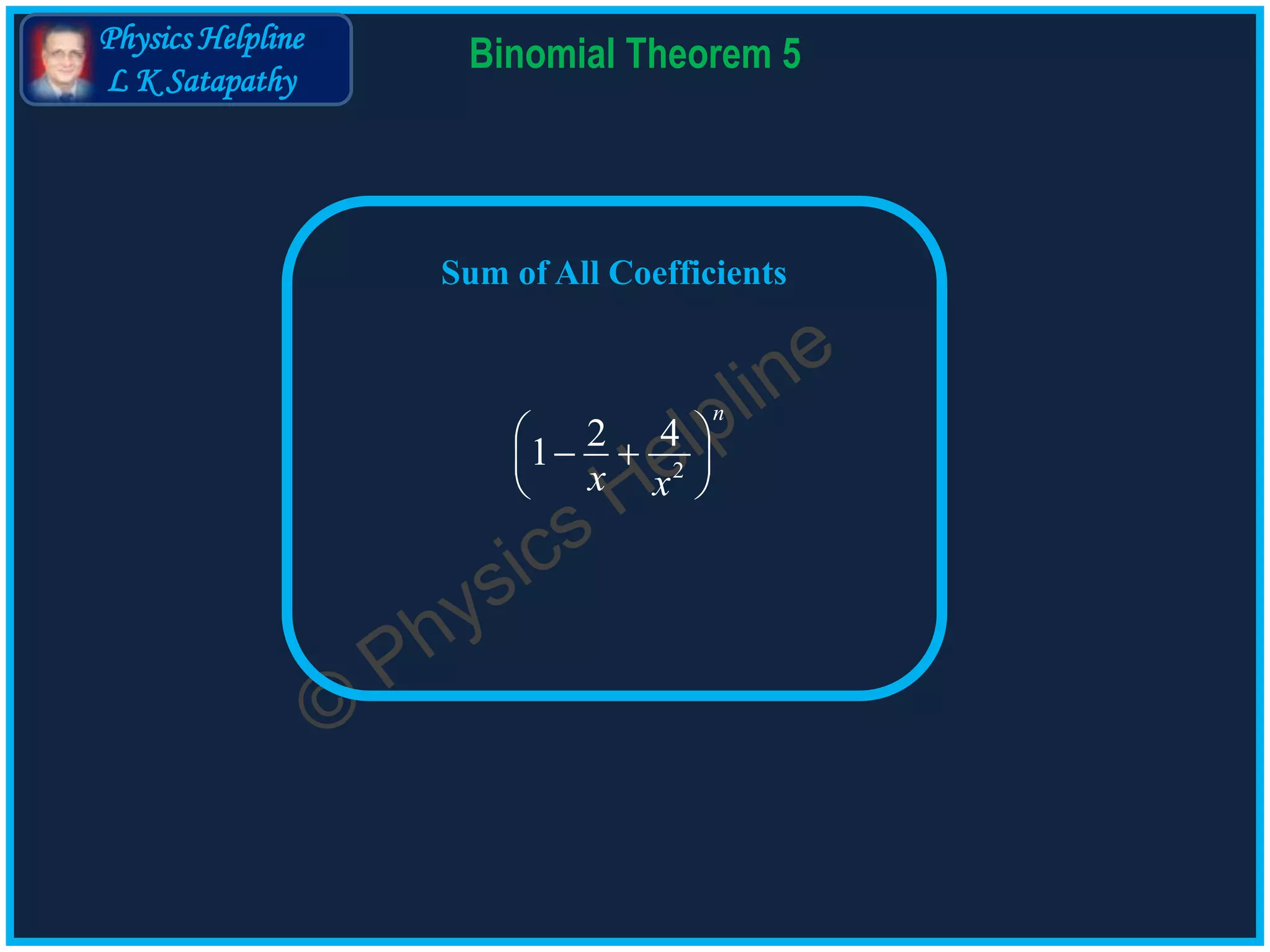
Binomial Theorem 5
Given that the total number of terms in the expansion = 28
2( 1)( 2)
28 3 2 56
2
n n
n n
2
3 54 0 ( 9)( 6) 0n n n n
Either n = – 9 (not possible) or n = 6
1 2 2
0 2 2 2
2 4. . . 1
n
n
n
a a a
a
x xx x x
In the given expansion , powers of x will vary from 0 to – 2n
We write
0 1 2 21 . . . 1 2 4 3
n n
nx a a a a
For n = 6 , the sum of coefficients of all the terms
Correct option = (d)
Answer :
6
3 729 [ ]Ans
2
2 41
n
x x
](https://image.slidesharecdn.com/binomialtheorem5-160720015741/85/Binomial-Theorem-5-3-320.jpg)


The document discusses the binomial theorem, focusing on a specific problem involving the expansion with a total of 28 terms. It identifies the value of n as 6 and calculates the sum of the coefficients in the expansion. Additional resources and social media links for further information are provided.


![Physics Helpline
L K Satapathy
Binomial Theorem 5
Given that the total number of terms in the expansion = 28
2( 1)( 2)
28 3 2 56
2
n n
n n
2
3 54 0 ( 9)( 6) 0n n n n
Either n = – 9 (not possible) or n = 6
1 2 2
0 2 2 2
2 4. . . 1
n
n
n
a a a
a
x xx x x
In the given expansion , powers of x will vary from 0 to – 2n
We write
0 1 2 21 . . . 1 2 4 3
n n
nx a a a a
For n = 6 , the sum of coefficients of all the terms
Correct option = (d)
Answer :
6
3 729 [ ]Ans
2
2 41
n
x x
](https://image.slidesharecdn.com/binomialtheorem5-160720015741/85/Binomial-Theorem-5-3-320.jpg)
