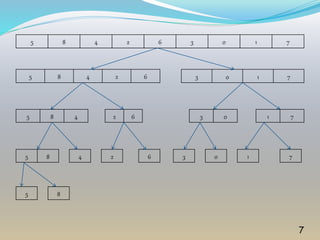
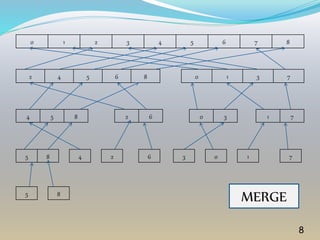
Merge sort is a sorting algorithm that works by recursively dividing an array into two halves, sorting each half, and then merging the sorted halves into a single sorted array. It has a time complexity of O(n log2n) and requires double the storage space of the original array. The key aspects are dividing the array, sorting the sub-arrays, and merging the sorted sub-arrays back together.

1. 1

2. Sharmin Sultana Jeesa
ID#141-15-3219
Dept: CSE
Course Code: CSE221
2

3. 3

4. * The key to Merge Sort is merging two sorted lists
into one, suchthat if you have two lists L1= {3, 8, 9}
& L2= {1, 5, 7} then the sorted array will be, merge(L1,
L2) = {1, 3, 5, 7, 8, 9}.
* Time complexity of merge sort is O(n log₂n).
* Double storage neededto hold the array to be
sorted.
4

5. 5
*Invented by John von
Neumann (1903-1957).
*Follows divide and
conquer approach.

6. * Divide: Divide the unsortedlist intotwo sub lists of
about half the size.
* Conquer: Sort each of the two sub lists recursively until
we have list sizes of length 1, in which case the list itself is
returned.
* Combine: Merge the two-sortedsub lists back into one
sorted list.
6

7. 5 8 4 2 6 3 0 1 7
7
5 8 4 2 6 3 0 1 7
5 8 4 2 6 3 0 1 7
85
5 8 4 2 6 3 0 1 7

8. 0 1 2 3 4 5 6 7 8
8
2 4 5 6 8 0 1 3 7
5 8 4 2 6 3 0 1 7
85
4 5 8 2 6 0 3 1 7
MERGE

9. Merge sort’s merge operation is useful in online
sorting, where the list to be sorted is received a
piece at a time, instead of all at the beginning.
In this We sort each new piece that is received using
any sorting algorithm, and then merge it into our
sorted list so far using the merge operation.
9

10. 10