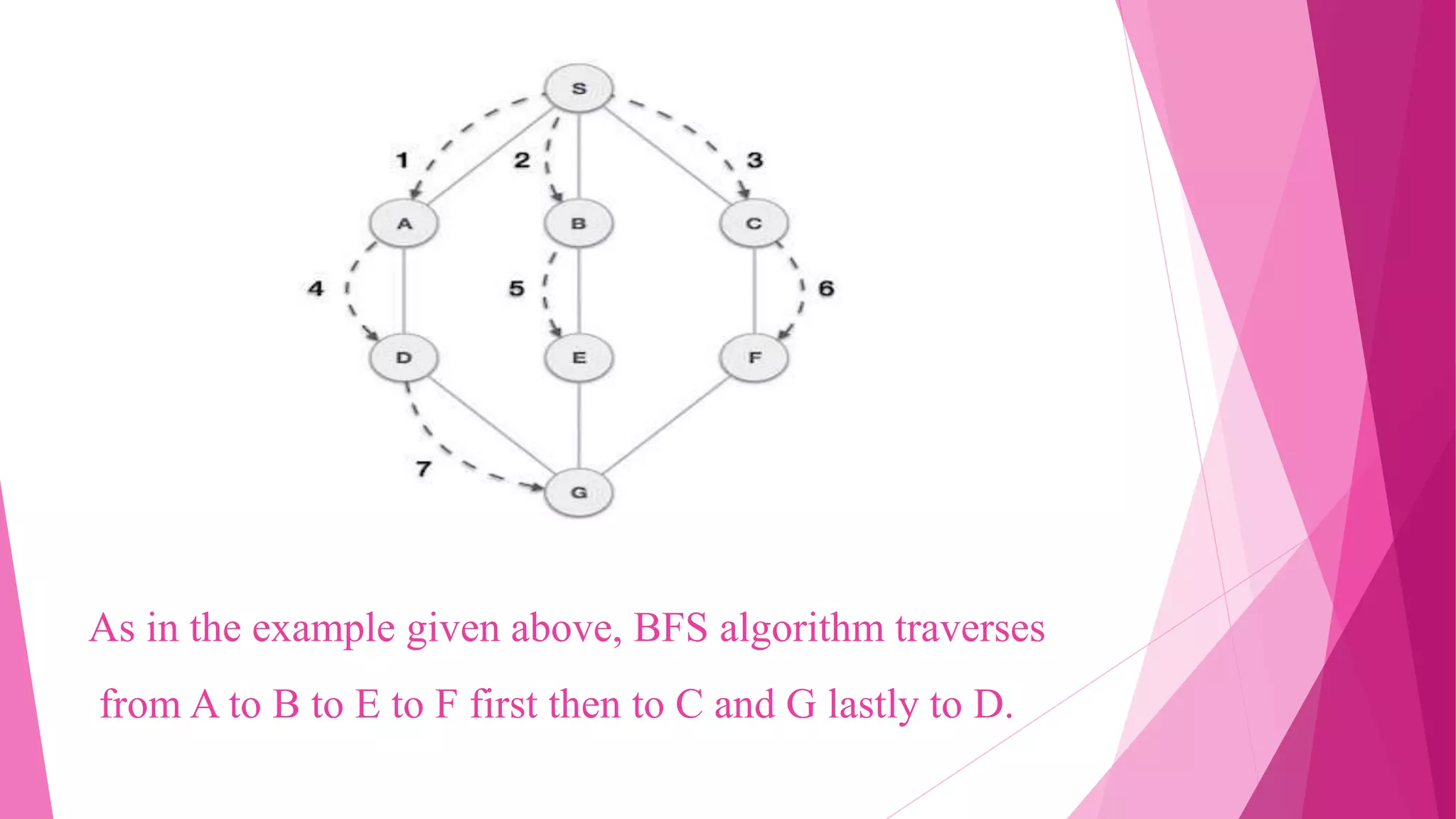
This document provides an overview of the Breadth-First Search (BFS) graph traversal algorithm. It begins by explaining that BFS starts at the root node and explores all neighboring nodes, selecting the nearest unexplored node at each step. It then provides examples of BFS traversing different graphs and describes the key aspects of the BFS algorithm, including maintaining a queue, coloring nodes as white/gray/black to track explored status, and updating distance and predecessor values at each step. In the end, it analyzes the properties of BFS, such as finding the shortest path distances, and discusses applications like finding connected components.

1. Welcome to Data Structure and
Algorithm Presentation
Breadth First Search (BFS)
By,
R.ISHWARIYA, M.sc(cs).,

2. Breadth First Search (BFS)
Breadth first search is a graph traversal algorithm that
starts traversing the graph from root node and explores
all the neighbouring nodes. Then, it selects the nearest
node and explore all the unexplored nodes.
The algorithm follows the same process for each of the
nearest node until it finds the goal.

3. As in the example given above, BFS algorithm traverses
from A to B to E to F first then to C and G lastly to D.

4. Breadth First Search (BFS)
 Breadth-first search starts at a given vertex s, which is at
level 0.
 In the first stage, we visit all the vertices that are at the
distance of one edge away. When we visit there, we
paint as "visited," the vertices adjacent to the start vertex
s - these vertices are placed into level 1.

5. Breadth First Search (BFS) Conti…..
 In the second stage, we visit all the new vertices we can
reach at the distance of two edges away from the source
vertex s. These new vertices, which are adjacent to level
1 vertices and not previously assigned to a level, are
placed into level 2, and so on.
 The BFS traversal terminates when every vertex has
been visited.

6. Breadth First Search (BFS)
 The algorithm maintains a queue Q to manage the set of
vertices and starts with s, the source vertex.
 Initially, all vertices except s are colored white, and s is gray.
 BFS algorithm maintains the following information for each
vertex u:

7. color[u] (white, gray, or black) : indicates status
- white = not discovered yet
- gray = discovered, but not finished
- black = finished
- d[u] : distance from s to u
- π[u] : predecessor of u in BF tree
Each vertex is assigned a color.
In general, a vertex is white before we start processing it, it is gray during the period
the vertex is being processed, and it is black after the processing of the vertex is completed.

8. BFS Algorithm
 Inputs: Inputs are a graph(directed or undirected) G =(V, E) and a
source vertex s, where s is an element of V. The adjacency list
representation of a graph is used in this analysis.
 Outputs: The outputs are a predecessor graph, which represents
the paths travelled in the BFS traversal, and a collection of
distances, which represent the distance of each of the vertices
from the source vertex.

9. BFS Algorithm
1. for each u in V − {s}
2. do color[u] ← WHITE
3. d[u] ← infinity
4. π[u] ← NIL
5. color[s] ← GRAY
6. d[s] ← 0
7. π[s] ← NIL
8. Q ← {}
9. ENQUEUE(Q, s)
10. while Q is non-empty
11. do u ← DEQUEUE(Q)
12. for each v adjacent to u
13. do if color[v] ← WHITE
14. then color[v] ← GRAY
15. d[v] ← d[u] + 1
16. π[v] ← u
17. ENQUEUE(Q, v)
18. DEQUEUE(Q)
19. color[u] ← BLACK

10. 1. Enqueue (Q,s)
2. while Q ≠
3. do u Dequeue(Q)
4. for each v adjacent to u
5. do if color[v] = white
6. then color[v] gray
7. d[v] d[u] + 1
8. [v] u
9. Enqueue(Q,v)
10. color[u] black
Note: If G is not connected, then BFS will not visit the entire graph
(without some extra provisions in the algorithm)

11. EXAMPLE: BFS FOR DIRECTED GRAPH

12. EXAMPLE: BFS FOR UNDIRECTED
GRAPH

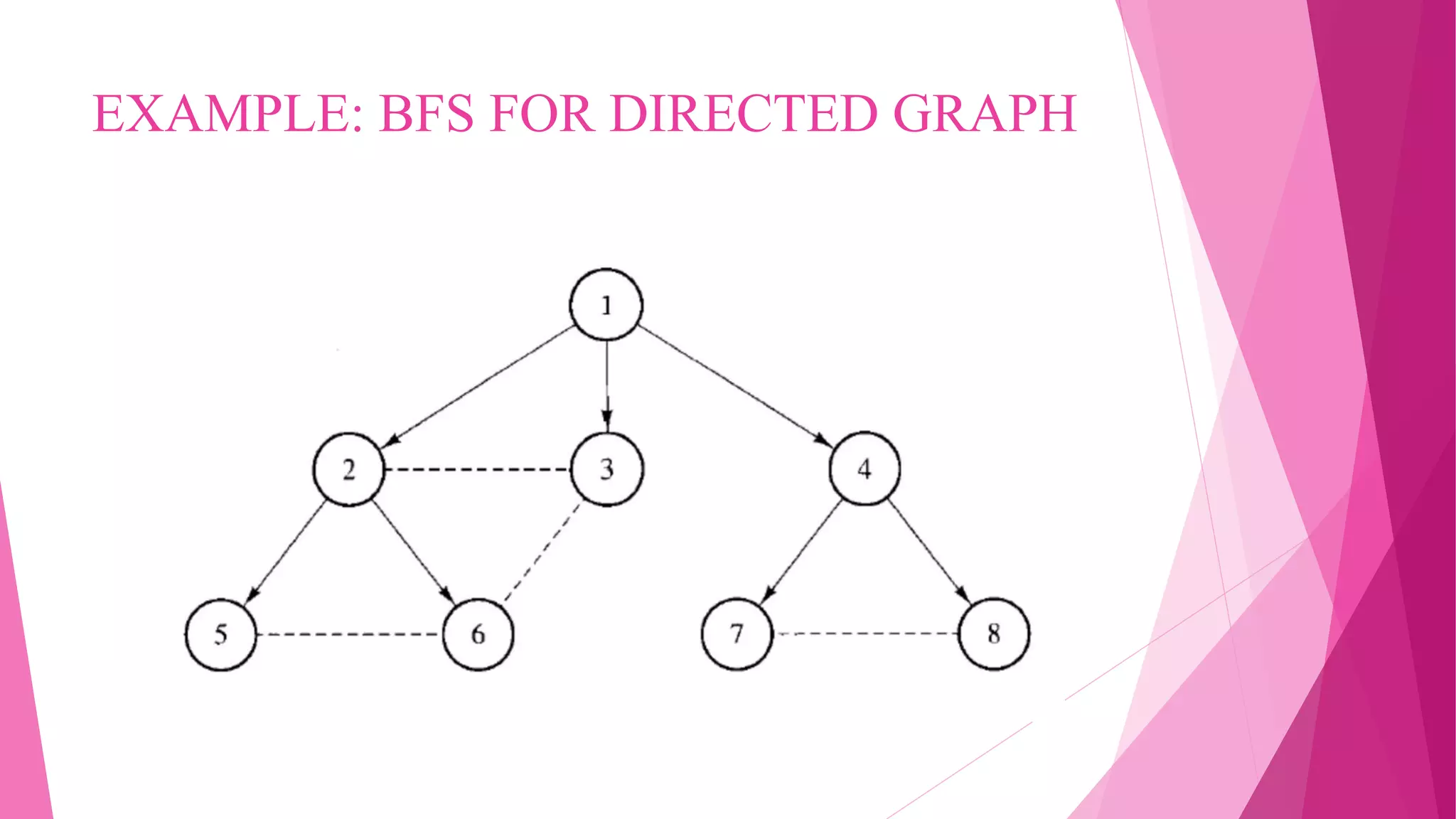
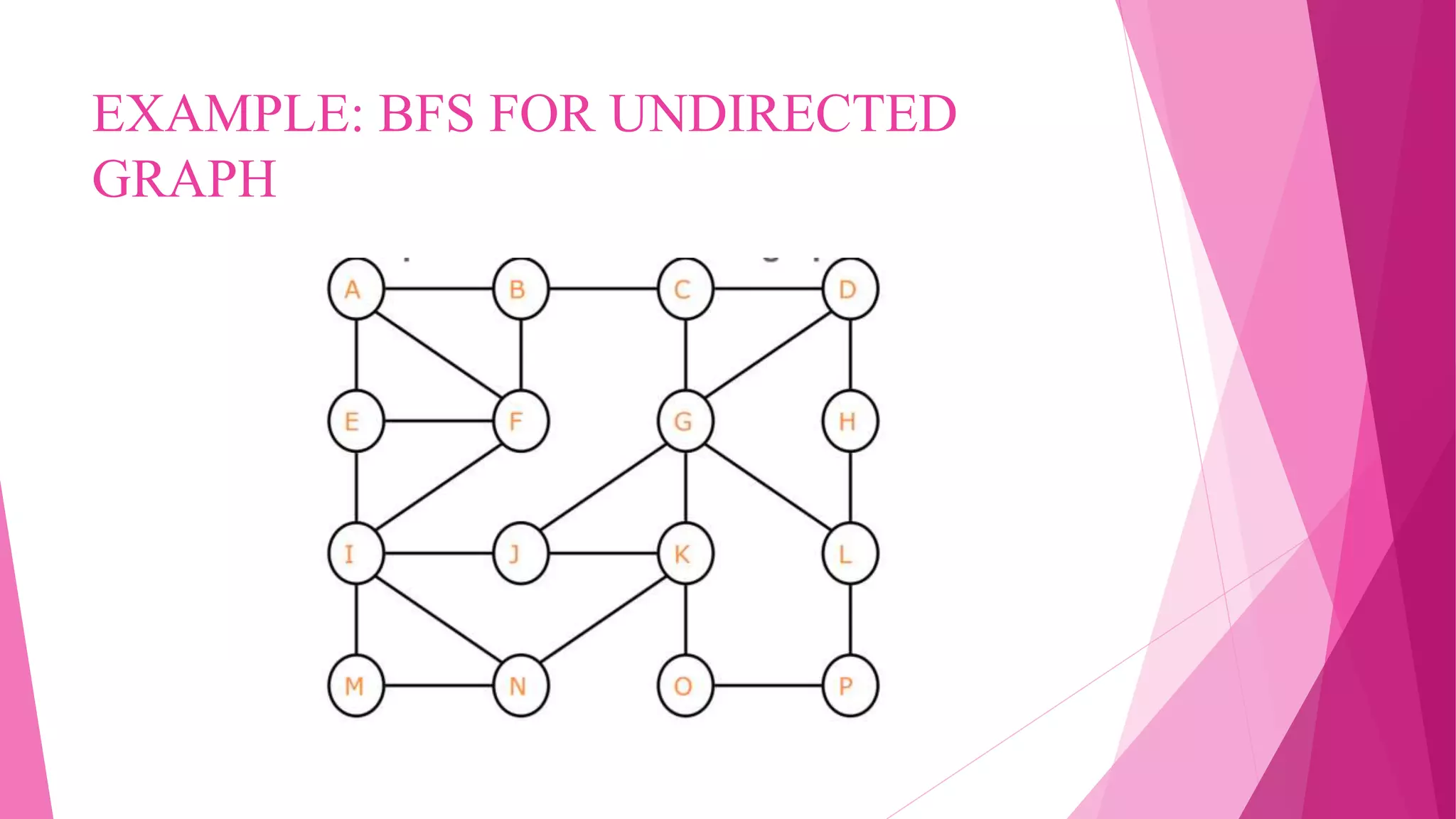
13. Analysis of Breadth-First Search
 Shortest-path distance (s,v) : minimum number of edges in any
path from vertex s to v. If no path exists from s to v, then (s,v) =
∞
 The ultimate goal of the proof of correctness is to show that d[v]
= (s,v) when the algorithm is done and that a path is found from s
to all reachable vertices.

14. Applications of BFS
Connected components
 Bipartite