1) Fixed point numbers represent integers in a binary format using a fixed number of bits. They have limited range but are fast and inexpensive to implement. Floating point numbers use exponents to represent a wider range of values with varying precision levels. 2) Common data types include short (16-bit integer), int (32-bit integer), float (32-bit floating point), and double (64-bit floating point). Floating point values follow IEEE standards and use significands and exponents. 3) Single precision floating point uses 32 bits with 24 bits for the significand, while double precision uses 64 bits with 53 bits for the significand, allowing wider ranges of values to be represented.

1. Digital Logic Circuits, Digital
Component and Data
Representation
Course: BCA-2nd
Sem
Subject: Computer Organization
And Architecture
Unit-1 1

2. Fixed point numbers[1]
• Fast and inexpensive implementation
• Limited in the range of numbers
• Susceptible to problems of overflow
•In a fixed-point processor, numbers are represented in integer
format.
• Fixed-point numbers and their data types are
characterized by their -
word size in bits
binary point
and
whether they are signed or unsigned

3. Fixed point numbers
• The dynamic range of an N-bit number based on 2’s-
complement representation is between -(2N-1
) & (2N-1
- 1), or
between -32,768 and 32,767 for a 16-bit system.
• By normalizing the dynamic range between -1 and 1, the range
will have 2N
sections, 2 -(N-1)
-size of each section starting at -1
up to 1 – 2 -(N-1).
• For a 4-bit system, there would be 16 sections, each of size
1/8, from -1 to 7/8 .

4. • In unsigned integer
the stored number can take on any integer value from 0
to 65,535.
• signed integer
uses two's complement
allows negative numbers
it ranges from -32,768 to 32,767
• With unsigned fraction notation
65,536 levels spread uniformly between 0 and 1
• the signed fraction format
allows negative numbers, equally spaced between -1
and 1

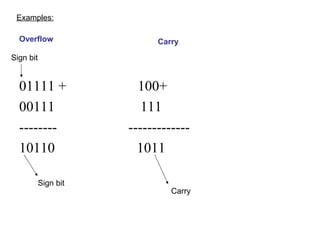
5. • Carry applies to unsigned numbers — when adding or
subtracting, result is incorrect.
• Overflow applies to signed numbers — when adding or
subtracting, result is incorrect.
Carry and Overflow[2]

6. 01111 + 100+
00111 111
-------- -------------
10110 1011
Overflow Carry
Sign bit
Carry
Examples:
Sign bit

7. Fractional Fixed Point Rep

8. Fractional Fixed Point Rep
• Rather than using the integer values just
discussed, a fractional fixed-point number that
has values between +0.99 . . . and -1 can be
used.

9. Data types[3]
1.Short:
it is of size 16 bits represented as 2’s complement with a
range from -215
to (215
-1)
2.Int or signed int:
it is of size 32 bits represented as 2’s complement with a
range from -231
to ( 231
-1)
3.Float:
it is of size 32 bits represented as IEEE 32 bit with a range
from 2-126
(1.175494x10-38
) to 2+128
(3.40282346x1038
)
4.Double:
it is of size 64 bits represented as IEEE 64 bit with a range
from 2-1022
(2.22507385x10-308
) to 2 1024
(1.79769313x10308
)

10. Floating-point representation
•The advantage over fixed-point representation is that
it can support a much wider range of values.
• The floating-point format needs slightly more storage
• The speed of floating-point operations is measured in
FLOPS.

11. General format of floating point number :
X= M. be
where M is the value of the significand (mantissa),
b is the base
e is the exponent.
Mantissa determines the accuracy of the number
Exponent determines the range of numbers that can be
represented
Floating-point representation

12. Floating point numbers can be represented as:
Single precision :
• called "float" in the C language family
• it is a binary format that occupies 32 bits
• its significand has a precision of 24 bits
Double precision :
• called "double" in the C language family
• it is a binary format that occupies 64 bits
• its significand has a precision of 53 bits
Floating-point representation

13. Single Precision (SP):
Bit 31 represents sign bit
Bits 23 to 30 represents exponent bits
Bits 0 to 22 represents fractional bits
Numbers as small as 10-38
and as large as10 38
can be represented
S e f
022233031

14. Double precision (DP) :
• since 64 bits, more exponent and fractional bits are available
• a pair of registers are used
Bits 0 to 31 of first register represents fractional bits
Bits 0 to 19 second register also represents fractional bits
Bits 20 to 30 represents exponent bits
Bits 31 is the sign bit
Numbers as small as 10 -308
and as large as 10 +308
can be represented
ffes
031019203031

15. • Instructions ending in SP or DP represents single and double precision
• Some Floating point instructions have more latencies than fixed point
instructions
Eg: MPY requires one delay
MPYSP has three delays
MPYDP requires nine delays
• Single precision floating point value can be loaded into a single
register where as Double precision values need a pair of registers
A1:A0, A3:A2 ,…….. B1:B0, B3:B2 ,……………
• C6711 processor has a single precision reciprocal instruction RCPSP
for performing division

16. References
1. Computer Organization and Architecture,
Designing for performance by William Stallings,
Prentice Hall of India.
2. Modern Computer Architecture, by Morris Mano,
Prentice Hall of India.
3. Computer Architecture and Organization by John P.
Hayes, McGraw Hill Publishing Company.
4. Computer Organization by V. Carl Hamacher,
Zvonko G. Vranesic, Safwat G. Zaky, McGraw Hill
Publishing Company.