Digital Electronics

Chapter 1
Introduction to Digital Systems
A digital system is a combination of devices designed to process the information in binary form.
The digital systems are widely used in almost all areas of life. The best example of digital system is a
general purpose digital computer. Other examples include digital displays, electronic calculators,
digital watch, digital counters, digital voltmeters, digital storage oscilloscope, telecommunication
systems and so on.
1.1 Advantages of Digital Systems
1. Ease of design: In digital circuits, exact values of the quantities are not important. The quan-
tities takes two discrete values i.e logic HIGH or logic LOW. The behaviour of small circuits
can be visualised without any special insights about the operation of the components. So
the digital systems are easier to design.
2. Ease of storage: The digital circuits uses latches that can hold on digital information as long
as it is necessary. Using the mass storage techniques, it is easier to store billions of bits of
information in a relatively small physical space.
3. Immune to noise: The noise is not critical in digital systems because the exact values of
quantities are not important. But the noise should not be large enough such that it prevents
us to distinguish between the logic High and logic LOW.
4. Accuracy and Precision: The digital information does not deteriorate or effected by noise
while processing. So the accuracy and precision are easier to maintain in a digital system.
5. Programmability: The operation of digital systems is controlled by writing programs. The
digital design is carried out by Hardware Description Languages(HDLs), using which the
structure and functioning of digital circuit is modelled and the behaviour of the designed
model is tested before built into the real hardware.
6. Speed: The digital devices uses the Integrated Circuits(ICs)in which the single transistor can
switch in a few pico seconds. Using these ICs, a digital system can process the input infor-
mation and produces an output in few nanoseconds.
7. Economy: Large number of digital circuits are integrated into a single chip such that it
provides lot of functionality in a small physical space. So the digital systems can be mass-
produces at a low cost.
1

2 CHAPTER 1. INTRODUCTION TO DIGITAL SYSTEMS
1.2 Limitations of Digital Systems
The real world is analog: The quantities that are to be processed by a digital system are analog
in nature example temperature, pressure, velocity etc. The input quantities must be converted to
digital form before processing and the processed digital output must be converted to analog as
shown in the figure 1.1. The conversion of information from digital to analog domain will take
time and can add complexity and expense to a system.
Figure 1.1: Block diagram of digital system
1.3 Building Blocks of Digital Systems:
The best example of digital system is a computer. The standard block diagram of a computer
consists of
1. Central Processing Unit(CPU): It does all the computations and processing.
2. Memory: It stores the program and data.
3. I/O Units: These units define how the input is fed into the computer and how to get the
output from the computer.
The CPU can further be divided into arithmetic and logic unit(ALU), control logic and registers
to store results. The ALU is made up of adders, subtracters, multipliers etc to form arithmetic and
logical operations. The functional blocks of ALU are made up of logic gates. The gate is a logical
building block which has 2 inputs and an output, so depending upon the gate type the output is
defined in terms of the input. Further, the gate is made up of transistors, capacitors etc. These
active and passive elements are the basic units of actual circuits. Thus the digital system can be
broken down into subsystems, subsystems can be broken down into modules, modules can be
broken down into functional blocks, functional blocks can be broken down into logic units, logic
units can be broken down into circuits and the circuits are made up of devices and components.

Chapter 2
Digital Number Systems and Codes
A digital system uses many number systems. The commonly used are decimal, binary, octal and
hexadecimal systems. These number systems are used in everyday life and they are called posi-
tional numbering system, since each digit of a number has an associated weight. The value of the
number is the weighted sum of all the digits.
1. Decimal Number System: This is the most commonly used number system that has 10 digits
from 0,1,2,3,4,5,6,7,8 and 9. The radix of decimal system is 10, so it is also called base-10 sys-
tem. The decimal number system is not convenient to implement a digital system, because
it is very difficult to design electronic devices with 10 different voltage levels.
2. Binary Number System: All the digital systems uses the binary number system as the basic
number system of its operations. The radix of binary system is 2, so it is also called base-2
system. It has only 2 possible values 0 and 1. A binary digit is called as bit. A binary number
can have more than 1 bit. The left most bit is called as least significant bit(LSB) and the right
most bit is called as most significant bit(MSB). It is easy to design simple, accurate electronic
circuits that operate with only 2 voltage levels using the binary number system. Binary data
is extremely robust in transmission because noise can be rejected easily. Binary number
system is the lowest possible base system, so any higher order counting system can be easily
encoded.
3. Octal and Hexadecimal Number System: The radix of octal number system is 8 and radix
of hexadecimal is 16. The octal number systems needs 8 digits, so it uses the digits 0-7 of
decimal system. The hexadecimal needs 16 digits, so it supplements decimal digits 0-9 with
the letters A-F. The octal and hexadecimal number system are useful for the representation
of multiple bits because their radices are powers of 2. A string of 3 bits can be uniquely rep-
resented by an octal digit. Similarly, a string of 4 digits can be represented by an hexadecimal
digit. Hexadecimal number system is widely in microprocessors and microcontrollers.
2.1 General Positional Number System
The value of a number in any radix is given by the formula
D =
p−1
i=−n
di ri
(2.1)
where r is the radix of the number, p is the number of digits to the left of radix point, n is the
number of digits to the right of radix point and di is the ith
digit of the number. The decimal value
of the number is determined by converting each digit of the number to its radix-10 equivalent and
3

4 CHAPTER 2. DIGITAL NUMBER SYSTEMS AND CODES
expanding the formula using radix-10 arithmetic.
Example 1: (331)8 = 3x82
+3x81
+1x80
= 192+24+1 = (217)10
Example 2: (D9)16 = 13x161
+9x160
= 208+9 = (217)10
2.2 Addition and Subtraction of Numbers
Addition and subtraction uses the same technique of general decimal numbers, only difference is
the use of binary numbers. To add two binary numbers, the least signiﬁcant bits of two numbers
are added with an initial carry cin = 0 to produce sum(s) and carry(cout ) as shown in the Table 2.1.
Then the process of adding is continued by shifting to the bits towards left till it reaches most sig-
niﬁcant bit and the carry in for each addition process is the carry out of the previous bits addition.
cin a b s cout
0 0 0 0 0
0 0 1 1 0
0 1 0 1 0
0 1 1 0 1
1 0 0 1 0
1 0 1 0 1
1 1 0 0 1
1 1 1 1 1
Table 2.1: Binary addition
Example: Addition of two numbers in decimal and binary number system.
decimal binary
carry 100 01111000
a 190 10111110
b 141 10001101
sum 331 101001011
The binary subtraction is carried out similar to the binary addition with carries replaced with
borrows and produces the difference(d) and the borrow out(bout ) as shown in the Table 2.2.
bin a b d bout
0 0 0 0 0
0 0 1 1 1
0 1 0 1 0
0 1 1 0 0
1 0 0 1 1
1 0 1 0 1
1 1 0 0 0
1 1 1 1 1
Table 2.2: Binary subtraction
Example: Subtraction of two numbers in decimal and binary number system.

2.3. REPRESENTATION OF NEGATIVE NUMBERS 5
decimal binary
borrow 100 01111100
a 229 11100101
b - 46 - 00101110
difference 183 10110111
The subtraction is commonly used in computers to compare two numbers. For example, if the
operation (a-b) produces a borrow out, then a is less than b, otherwise, a is greater than or equal
to b.
2.3 Representation of Negative Numbers
The positive numbers and negative numbers in decimal system are indicated by + and − sign
respectively. This method of representation is called as sign-magnitude representation. But those
signs are not convenient for representing binary numbers. There are many ways to represent
signed binary numbers.
2.3.1 Signed-Magnitude Representation
The signed magnitude system uses extra bit to represent the sign. Positive number is represented
by ’0’ and negative number by ’1’. The most significant digit is used as the sign bit and lower bits
contains the magnitude. The following are the examples of 8-bit signed binary integers and their
decimal equivalents.
Example 1: (01010101)2 = +(85)10 and (11010101)2 = −(85)10
Example 2: (01111111)2 = +(127)10 and (11111111)2 = −(127)10
Example 3: (00000000)2 = +(0)10 and (10000000)2 = −(0)10
Since zero can be represented in two possible ways, there are equal number of positive and nega-
tive integers in signed magnitude system. An n-bit signed magnitude integer lies within the range
−(2n−1
−1) to +(2n−1
−1). The signed magnitude representation in digital logic circuit requires to
examine the signs of the addends. If the signs are same, it must add the magnitudes and if the signs
are different, it must subtract smaller from the larger magnitude and give the result with sign of
larger integer. This method will increase the complexity of the logic circuit, so it is not convenient
for hardware implementations.
2.3.2 Complement Number Systems
The complement number negates a number by taking its complement as defined by the system.
The advantage of this system over signed-magnitude representation is that the two numbers in
complement number system can be added or subtracted without the sign and magnitude checks.
There are two complement number systems viz. the radix-complement and the diminished radix-
complement. The complement number system has fixed number of digits,say n. If an operation
produces more than n digits, then the extra higher order bits are omitted.
2.3.3 Radix Complement Representation
The radix complement of an n-digit number is obtained by subtracting it from rn
, where r is the
radix. In decimal system, radix-complement is called 10 s complement. For example, the 10 s

complement of 127 = 103
− 127 = 873. If the number is between the range 1 and rn
− 1, the sub-
traction results in another number in the same range. By definition, radix-complement of 0 is
rn
, which has n + 1 digits. The extra bit is omitted which results in 0 and thus there is only one
radix-complement representation of zero.
By definition, subtraction operation is required to obtain radix-complement. To avoid subtrac-
tion, we can rewrite rn
as rn
= (rn
− 1) + 1 and rn
− D = ((rn
− 1) − D) + 1, where D is the n-digit
number. The number (rn
− 1) is the highest n-digit number. Let the complement of digit d is
r − 1 − d, then the radix-complement is obtained by complementing individual digits of D and
adding 1.
Example: 10 s complement of 4-digit number, 0127 = 9872+1 = 9873.
Two’s Complement Representation The radix complement for binary numbers is called the 2 s
complement. The Most Significant Bit(MSB) represents the sign. If it is 0, then the number is pos-
itive and if it is 1, the number is negative. The remaining (n −1) bits represents the magnitude, but
not as simple weighted number. The weight of the MSB is −2n−1
instead of +2n−1
.
Example 1: 1510 = (01111)2, 2 s complement of (01111)2 = (10000+1) = (10001)2 = −1510.
Example 2: −12710 = (10000001)2, 2 s complement of (10000001)2 = (01111110+1) = (01111111)2 =
+12710.
Example 3: 010 = (0000)2, 2 s complement of (0000)2 = (1111+1) = (0000)2+carry 1 = 010.
The carry out bit is ignored in 2 s complement operations, so the result is the lower n bits. Since
zero’s sign bit is 0, it is considered as positive and zero has only one representation in 2 s comple-
ment system. Hence, the range of representable numbers is from −2n−1
to +(2n−1
−1). The two’s
complement system can be applied to fractions as well.
Example: 2 s complement of +19.312510 = (010011.0101)2 = 101100.1010 + 1 = (101100.1011)2 =
−19.312510.
Sign Extension An n-bit two’s complement number can be converted to m-bit one. If m > n, pad
a positive number with 0s and negative number with 1s. If m < n, discard (n − m) leftmost bits,
but the result is valid only if all the discarded bits are the same as the sign bit of the result.
2.3.4 Diminished Radix-complement Representation
The diminished radix-complement of n-digit number is obtained by subtracting it from (rn
− 1).
This is obtained by complementing individual digits of the number. In decimal system, it is called
as 9 s complement.
One’s Complement Representation The diminished radix-complement for binary numbers is
called as one’s complement. The MSB represents the sign. If it is 0, the number is positive and the
remaining (n −1) bits directly indicate the magnitude. If MSB is 1, the number is negative and the
complement of remaining (n −1) bits is the magnitude of the number. The positive numbers have
same representation in both one’s and two’s complements, but negative number representation
differs by 1. The weight of the MSB is −(2n−1
−1) for computing decimal equivalents.
Example 1: One’s complement of 410 = (0100)2is(1011)2 = −410.
Example 2: One’s complement of 010 = (0000)2is(111)2 = −010.
There are two representation of zero, positive and negative zero. So, the range of representation is
−(2n−1
−1) to +(2n−1
−1).
The main advantage of the one’s complement is that it is easy to complement. But design
of adders is difficult than two’s complement. Since zero has two representations,zero detecting
circuits must check for both representations of zero.

2.4. EXCESS REPRESENTATIONS 7
2.4 Excess Representations
In excess representation, a bias B is added to the true value of the number to produce an excess
number. Consider a m-bit string whose unsigned integer value is M(0 ≤ M < 2m
), then in excess-
B representation the m-bit string represents the signed integer (M −B), where B is the bias of the
number system. An excess-2m−1
system represents any number X in the range −2m−1
to +2m−1
−1
by the m-bit binary representation of X +2m−1
, which is always non-negative and less than 2m
.
Example:Consider 3-bit number say (110)2, the unsigned value is 610. Then the excess-4(bias is
23−1
) representation is (110−100)2 = (010)2 = −610.
The representation of number in excess representation and two’s complement is identical ex-
cept for the sign bits, which are always opposite. The excess representation are most commonly
used in floating-point number systems.
2.5 Two’s-Complement Addition and Subtraction
2.5.1 Addition
Addition is performed by doing the simple binary addition of the two numbers.
Examples:
decimal binary decimal binary
+3 0011 +4 0100
++4 + 0100 +-7 + 1001
+7 0111 -3 1101
If the result of addition operation exceeds the range of the number system, overflow occurs.
Addition of two numbers with like signs can produces overflow, but addition of two numbers with
different signs never produces overflow.
Examples:
-3 1101 +7 0111
+-6 + 1010 ++7 + 0111
-9 10111 +14 1110
2.5.2 Subtraction
Subtraction is accomplished by first performing two’s complement of the subtrahend and then
adding it to the minuend.
+4 0100 +3 0011
-+3 + 1100 –4 + 0011
+3 10001 +7 0111
Overflow in subtraction can be detected by examining the signs of the minuend and the com-
plemented subtrahend same as addition. The extra bit can be ignored, provided range is not ex-
ceeded.

2.6 One’s Complement Addition and Subtraction
The addition operation is performed by standard binary addition, if there is a carry out of the MSB,
then add 1 to the result. This rule is called en-around carry. Similarly, subtraction is accomplished
by first performing the complement of the subtrahend and proceed as in addition. Since zero has
two representations, the addition of a number and its one’s complement produces negative zero.
Example:
decimal binary
+6 0110
+-3 + 1100
+3 10010
+ 1
0011
2.7 Binary Codes
When an information is sent over long distances, the channel through which it is sent may dis-
tort the transmitted information. It becomes necessary to modify the information into some form
before sending and then convert at the receiving end to get back the original information. This
process of altering the characteristics of information to make it suitable for the intended applica-
tion is called coding.
A set of n-bit strings in which different bit strings represent different numbers or other things is
called a code. A particular combination of n-bit values is called a code word. Normally n-bit string
can take 2n
values, but it is not necessary that it contains 2n
valid code words.
2.7.1 Binary Coded Decimal Code
There are ten symbols in the decimal number system from 0 to 9. So 4-bits are required to repre-
sent them in binary form. This process of encoding the digits 0 through 9 by their unsigned binary
representation is called Binary Coded Decimal(BCD) code. The code words from 1010 through
1111 are not used, they may used for error detection purpose. BCD is a weighted code because
decimal value of a code is the algebraic sum of the fixed weight to each bit. The weights of BCD
are 8, 4, 2 and 1, so the BCD is also called as 8421 code.
Example: (16.85)10 = (00010110.10000101)
There are many possible weights to write a number in BCD code to make the code suitable
for specific application. One such code is the 2421 code in which the code word for the nine’s
complement of any digit may be obtained by complementing the individual bits of code words. So
2421 code is called self-complementing codes.
Example: 2421 code of 410 = 0100. Its complement is 1011 which is 2421 code for 510 = (9−4)10.
Excess-3 code is the self-complementing code which is not weighted. It is obtained by adding
0011 to all the 8421 code. The code words follow a standard binary sequence, so this can be used
in standard binary counters.
Example: Excess-3 code of (0010)2 = (0010+0011) = (0101)2.

2.7. BINARY CODES 9
Addition of BCD digits is similar to adding 4-bit unsigned binary numbers, except that a
correction of 0110 is to made if the result is exceeds 1001.
Example:
decimal binary
8 10000
+8 + 1000
-16 10000
+ 0110
10110
The main advantage of the BCD code is the relative ease of converting to and from decimal.
Only the four-bit code for the decimal digits 0 through 9 need to be remembered. However, BCD
requires more bits to represent a decimal number of more than 1 digit because it does not use all
possible four-bit code words and is therefore somewhat inefficient.
2.7.2 Gray Code
There are many applications in which it is desirable to have a code in which adjacent codes differ
only in one bit. For example, in electromechanical applications such as braking systems, some-
times it is necessary for an input sensor to produce a digital value that indicates a mechanical po-
sition. Such codes are called unit distance codes. Gray code is one of the unit distance code. The
3-bit gray codes for corresponding decimal numbers are 010 = (000)2, 110 = (001)2, 210 = (011)2,
310 = (010)2, 410 = (110)2, 510 = (111)2, 610 = (101)2 and 710 = (100)2.
The most popular use of Gray codes is in electromechanical applications such as the position
sensing transducer known as shaft encoder. A shaft encoder consists of a disk in which concentric
circles have alternate sectors with reflective surfaces while the other sectors have non-reflective
surfaces. The position is sensed by the reflected light from a light emitting diode. However, there
is choice in arranging the reflective and non-reflective sectors. A 3-bit binary coded disk is as
shown in the Figure 2.1.
Figure 2.1: 3-bit binary coded shaft encoder
The straight binary code in the Figure 2.1 can lead to errors because of mechanical imperfections.
When the code is transiting from 001 to 010, a slight misalignment can cause a transient code of
011 to appear. The electronic circuitry associated with the encoder will receive 001 –> 011 -> 010.
If the disk is patterned to give Gray code output, the possibilities of wrong transient codes will not
arise. This is because the adjacent codes will differ in only one bit. For example the adjacent code

for 001 is 011. Even if there is a mechanical imperfection, the transient code will be either 001 or
011. The shaft encoder using 3-bit Gray code is shown in the Figure 2.2.
Figure 2.2: 3-bit Gray coded shaft encoder disk
There are two convenient methods to construct Gray code with any number of desired bits.
The first method is based on the fact that Gray code is also a reflective code. The following rule
may be used to construct Gray code:
1. A one-bit Gray code had code words, 0 and 1.
2. The first 2n
code words of an (n + 1)-bit Gray code equal the code words of an n-bit Gray
code, written in order with a leading 0 appended.
3. The last 2n
code words of a (n +1)-bit Gray code equal the code words of an n-bit Gray code,
written in reverse order with a leading 1 appended.
However, this method requires Gray codes with all bit lengths less than n also be generated as a
part of generating n-bit Gray code. The second method allows us to derive an n-bit Gray code word
directly from the corresponding n-bit binary code word:
1. The bits of an n-bit binary code or Gray code words are numbered from right to left, from 0
to n-1.
2. Bit i of a Gray-code word is 0 if bits i and i +1 of the corresponding binary code word are the
same, else bit i is 1. When i +1 = n, bit n of the binary code word is considered to be 0.
2.7.3 Character Codes
Most of the information processed by a computer is non-numeric. The most common type of non-
numeric data is text and string of characters. Codes that include alphabetic characters are called
character codes. Each character is represented by a bit string. The most commonly used character
code is ASCII (American Standard Code for Information Interchange). Each character in ASCII is
represented with a 7-bit string, yielding total of 128 different characters. The code contains upper-
case and lowercase alphabet, numerals, punctuation and various non-printing control characters.
Example: ASCII code for A = 1000001, a = 1100001, ? = 0111111 etc.

Chapter 3
Boolean Algebra
In 1854, George Boole introduced a systematic treatment of logic and developed for this pur-
pose an algebraic system, now called Boolean Algebra. Boolean algebra is a system of mathemat-
ical logic. It is an algebraic system consisting of the set of elements(0,1), two binary operators
called OR, AND and one unary operator, NOT. It is the basic mathematical tool in the analysis and
synthesis of switching circuit. It is way to express logic functions algebraically.
3.1 Rules in Boolean Algebra
The important rules used in Boolean algebra are as follows:
1. Variable used can have only two values, Binary 1 for HIGH and Binary 0 for LOW.
2. Complement of a variable is represented by an over-bar. Thus, complement of variable B is
represented as ¯B. Thus if B = 0, then ¯B = 1 and if B = 1, then ¯B = 0.
3. OR of the variables is represented by a plus (+) sign between them. For example, OR of A, B
and C is represented as (A +B +C).
4. Logical AND of the two or more variable is represented by writing a dot between them such
as (A.B.C). Sometimes, the dot may be omitted and written as (ABC).
3.2 Postulates
The Postulates of a mathematical system form the basic assumption from which it is possible to
reduce the rules, theorems and properties of the system. The most common postulates used to
formulate various algebraic structures are as follows.
1. Associative law-1: A +(B +C) = (A +B)+C
This law states that ORing of several variables gives the same result regardless of the group-
ing of the variables, i.e. for three variables, (A OR B) ORed with C is same as A ORed with (B
OR C).
Associative law-2: (AB)C = A(BC) The associative law of multiplication states that it makes
no difference in what order the variables are grouped when ANDing several variable. For
three variables, (A AND B) ANDed with C is the same as A ANDed with (B AND C).
11

12 CHAPTER 3. BOOLEAN ALGEBRA
2. Commutative law-1: A +B = B + A
This states that the order in which the variables are ORed makes no difference in the output.
Therefore (A OR B) is same as (B OR A).
Commutative law-2: AB = B A
The commutative law of multiplication states that the order in which variables are ANDed
makes no difference in the output. Therefore (A AND B) is same as (B AND A).
3. Distributive law: A(B +C) = (AB + AC)
The distributive law states that ORing several variables and ANDing the result with single
variable is equivalent to ANDing the result with a single variable with each of the several
variables and then ORing the products.
4. Identity Law-1: A +0 = A
A variable ORed with 0 is always equal to the variable.
Identity Law-2: A.1 = A
A variable ANDed with 1 is always equal to the variable.
5. Inversion law: ¯¯A = A
This law uses the NOT operation. The inversion law states that double inversion of a variable
results in the original variable itself.
6. Closure
A set S is closed with respect to binary operator if, for every pair of elements of S, the binary
operator speciﬁes a rule for obtaining a unique element of S. For example, the set of natu-
ral number N=(1,2,3,4.......n) is closed with respect to the binary operator + by the rules of
arithmetic addition, since for any a,b N, there is a unique c N such that a +b = c. The set
of natural number is not closed with respect to the binary operator by rules of arithmetic
subtraction, because 2−3 = −1 and 2,3 N. But (−1) N.
7. Consensus theorem-1: AB + ¯AC +BC = AB + ¯AC
The (BC) term is called the consensus term and is redundant. The consensus term is formed
pair of terms in which a variable A and its complement ¯A are present. The consensus term
is formed by multiplying the two terms and leaving out the selected variable and its comple-
ment.
The consensus of AB + ¯AC is BC.
Proof:
AB + ¯AC +BC
= AB + ¯AC +BC(A + ¯A)
= AB + ¯AC +BC A + ¯ABC
= AB(1+C)+ ¯AC(1+B)
= AB + ¯AC
This theorem can be extended to any number of variabls.
Similarly, (A +B).( ¯A +B).(B +C) = (A +B).( ¯A +C)
8. Absorptive Law
This law enables a reduction in a complicated expression to a simpler one by absorbing like-
terms.
A +(A.B) = A (OR Absorption Law)
A(A +B) = A (AND Absorption Law)
9. Idempotence law: An input that is ANDed or ORed with itself is equal to that input.
A + A = A: A variable ORed with itself is always equal to the variable.

3.2. POSTULATES 13
A.A = A: A variable ANDed with itself is always equal to the variable.
10. Adjacency law:
(A +B)(A + ¯B) = A
A.B + A ¯B = A
11. Duality: In positive logic system, more positive of two voltage levels represented as 1 and
more negative by 0 . Whereas, in negative logic system, more positive is represented as 0
and more negative by 1 . The distinction between positive logic and negative logic system
is that the OR gate in the positive logic becomes an AND gate in negative logic system and
vice verse. The duality theorem applies when we are changing one logic system to another.
Duality theorem states that ’0’ becomes ’1’, ’1’ becomes ’0’, ’AND ’ becomes ’OR’ and ’OR’
becomes ’AND’. The variables are not complemented in this process.
Given expression Dual
¯0 = 1 ¯1 = 0
0.1 = 0 1+0 = 1
0.0 = 0 1+1 = 1
1.1 = 1 0+0 = 0
A.0 = 0 A +1 = 1
A.A = A A + A = A
A.1 = A A +0 = A
A. ¯A = 0 A + ¯A = 1
A.B = B.A A +B = B + A
A.(B +C) = AB + AC A +BC = (A +B)(A +C)
12. DeMorgan’s Theorem :
DeMorgan suggested two theorems that form an important part of boolean algebra. In the
equation form, they are:
(a) AB = ¯A + ¯B
The complement of a product is equal to the sum of the complements. This is illus-
trated by the below truth table.
(b) (A +B) = ¯A. ¯B
The complement of sum is equal to product of complements. The following truth table
illustrates this law .

14 CHAPTER 3. BOOLEAN ALGEBRA
13. Redundant literal Rule
This law states that ORing of a variable with the AND of the complement of that variable with
another variable is equal to ORing of the two variable i.e
A + ¯AB = A +B
Another theorem based on this law is
A( ¯A +B) = AB
3.3 Theorems of Boolean Algebra
Theorem-1: x + x = x
x + x
= (x + x).1
= (x + x)(x + ¯x)
= x + x ¯x
= x +0
= x
Theorem-2: x.x = x
x +1
= 1.(x +l)
= (x + ¯x)(x +1)
= x + ¯x.1
= x + ¯x
= 1
x.0 = 0 by duality
Theorem-3: x + xy = x
x + xy = x.1+ xy
= x(1+ y)
= x(y +1)
= x.1
= x
x(x+y) = x by duality

Chapter 4
Logic Gate Families
Digital IC gates are classified not only by their logic operation, but also by specified logic circuit
family to which they belong. Each logic family has its own basic electronic circuit upon which
more complex digital circuit and functions are developed.
The first logic circuit was developed using discrete circuit components. Using advance tech-
niques, these complex circuits can be miniaturized and produced on a small piece of semicon-
ductor material like silicon. Such a circuit is called integrated circuit(IC). Nowadays, all the digital
circuits are available in IC form. While producing digital ICs, different circuit configurations and
manufacturing technologies are used. This results into a specific logic family. Each logic family
designed in this way has identical electrical characteristics such as supply voltage range, speed of
operation, power dissipation, noise margin etc. The logic family is designed by considering the
basic electronic components such as resistors,diodes, transistors and MOSFET or combinations
of any of these components. Accordingly, logic families are classified as per the construction of
the basic logic circuits.
4.1 Classification of logic families
Logic families are classified according to the principle type of electronic components used in their
circuitry as shown in the Figure 4.1. They are:
Bipolar ICs: which uses diodes and transistors(BJT).
Unipolar ICs: which uses MOSFETs.
Figure 4.1: Logic family classification
Out of the logic families mentioned above, RTL and DTL are not very useful due to some inherent
disadvantages. While TTL, ECL and CMOS are widely used in many digital circuit design applica-
tions.
15

16 CHAPTER 4. LOGIC GATE FAMILIES
4.2 Transistor-Transistor Logic(TTL)
TTL is the short form of Transistor Transistor Logic. As the name suggests they refers to the digital
integrated circuits that employ logic gates consisting primarily of bipolar transistors. The most
basic TTL circuit is an inverter. It is a single transistor with its emitter grounded and its collector
tied to VCC with a pull-up resistor, and the output is taken from its collector. When the input is
high (logic 1), the transistor is driven to saturation and the output voltage i.e. the drop across the
collector and emitter is negligible and therefore output voltage is low(logic 0).
A two input NAND gate can be realized as shown in the figure 4.2. When, at least any one of the
input is at logic 0, the multiple emitter base junctions of transistor TA are forward biased where as
the base collector is reverse biased. The transistor TA would be ON forcing a current away from the
base of TB and thereby TB is OFF. Almost all Vcc would be dropping across an OFF transistor and
the output voltage would be high(logic l). For a case when both Input1 and Input2 are at Vcc, both
the base emitter junctions are reverse biased and the base collector junction of the transistor TA is
forward biased. Therefore, the transistor TB is on making the output at logic 0, or near ground.
Figure 4.2: A 2-input TTL NAND gate
However, most TTL circuits use a totem pole output circuit instead of the pull-up resistor as
shown in the Figure 4.3. It has a Vcc-side transistor(TC ) sitting on top of the GND-side output
transistor(TD). The emitter of the TC is connected to the collector of TD by a diode. The output
is taken from the collector of transistor TD. TA is a multiple emitter transistor having only one
collector and base. The multiple base emitter junction behaves just like an independent diode.
Applying a logic ’1’ input voltage to both emitter inputs of TA, reverse-biases both base-emitter
junctions, causing current to flow through RA into the base of TB , which is driven into saturation.
When TB starts conducting, the stored base charge of TC dissipates through the TB collector, driv-
ing TC into cut-off. On the other hand, current flows into the base of TD, causing it to saturate
and its collector emitter voltage is 0.2V and the output is equal to 0.2V, i.e. at logic 0. In addition,
since TC is in cut-off, no current will flow from Vcc to the output, keeping it at logic ’0’. Since TD
is in saturation, its input voltage is 0.8 V. Therefore the output voltage at the collector of transistor
TB is 0.8V +V CESat (saturation voltage between conductor and emitter of a transistor is equal
to 0.2V ) = 1V. TB always provides complementary inputs to the bases of TC and TD, such that TC
and TD always operate in opposite regions, except during momentary transition between regions.
The output impedance is low independent of the logic state because one transistor (either TC or
TD ) is ON. When at least one of inputs are at 0 V, the multiple emitter base junctions of transistor
TA are forward biased whereas the base collector is reverse biased and transistor TB remains off
and therefore the output voltage is equal to Vcc. Since the base voltage for transistor TC is Vcc, this
transistor is ON and the output is also Vcc and the input to transistor TD is 0 V, hence it remains
off.

4.3. CMOS LOGIC 17
Figure 4.3: A 2-input TTL NAND Gate with a totem pole output stage
TTL overcomes the main problem associated with DTL(Diode Transistor Logic) i.e. lack of speed.
The input to a TTL circuit is always through the emitter(s) of the input transistor, which exhibits a
low input resistance. The base of the input transistor, on the other hand, is connected to the Vcc,
which causes the input transistor to pass a current of about 1.6mA when the input voltage to the
emitter(s) is logic ’0’. Letting a TTL input ’ﬂoat’ (left unconnected) will usually make it go to logic
’1’. However, such a state is vulnerable to stray signals, which is why it is good practice to connect
TTL inputs to Vcc using 1kΩ pull-up resistors.
4.3 CMOS Logic
The term ’Complementary Metal-Oxide-Semiconductor(CMOS)’ refers to the device technology
for fabricating integrated circuits using both n-channel and p-channel MOSFETs. Today, CMOS is
the major technology in manufacturing digital IC’s and is widely used in microprocessors, mem-
ories and other digital IC’s. The input to a CMOS circuit is always to the gate of the input MOS
transistor. The gate offers a very high resistance because it is isolated from the channel by an ox-
ide layer. The current ﬂowing through a CMOS input is virtually zero and the device is operated
mainly by the voltage applied to the gate, which controls the conductivity of the device channel.
The low input currents required by a CMOS circuit results in lower power consumption, which is
the major advantage of CMOS over TTL. In fact, power consumption in a CMOS circuit occurs only
when it is switching between logic levels. Moreover, CMOS circuits are easy and cheap to fabricate
resulting in high packing density than their bipolar counterparts. CMOS circuits are quite vulner-
able to ESD damage, mainly by gate oxide punchthrough from high ESD(Electro Static Discharge)
voltages. Therefore, proper handling CMOS IC’s is required to prevent ESD damage and generally,
these devices are equipped with protection circuits.
Figure 4.4 shows the circuit symbols of an n-channel and a p-channel transistor. An nMOS tran-
sistor is ’ON’ if the gate voltage is at logic ’1’ or more precisely if the potential between the gate and
the source terminals(VGS) is greater than the threshold voltage VT . An ’ON’ transistor implies the
existence of a continuous channel between the source and the drain terminals. On the other hand,
an ’OFF’ nMOS transistor indicates the absence of a connecting channel between the source and
the drain. Similarly, a pMOS transistor is ’ON’ if the potential VGS is lower(or more negative) than
the threshold voltage VT .

Figure 4.4: Symbol of n-channel and p-channel transistors
Figure 4.5 shows a CMOS inverter circuit(NOT gate), where a p-channel and an n-channel MOS
transistor is connected in series. A logic ’1’ input voltage would make TP (p-channel) turn off and
TN (n-channel) turn on. Hence, the output will be low, pulling output to logic ’0’. A logic ’0’ Vin
voltage, on the other hand, will make TP turn on and TN turn off, pulling output to near VCC or
logic ’1’. The p-channel and n-channel MOS transistors in the circuit are complementary and they
are always in opposite states i.e. when one of them is ON the other is OFF.
Figure 4.5: CMOS inverter circuit
The circuit (a) in the ﬁgure 4.6 shows a 2-input CMOS NAND gate where the TN1 and TP1 have
the same input A and TN2 and TP2 has the same input B. When both the inputs A and B are high,
TN1 and TN2 are ON and TP1 and TP2 are OFF. Therefore, the output is at logic 0. On the other
hand, when both input A and input B are logic 0, TN1 and TN2 is OFF and TP1 and TP2 are ON.
Hence, the output is at VCC , logic 1. Similar situation arises when any one of the input is logic 0.
In such a case, one of the bottom series transistors i.e. either TN1 or TN2 would be OFF forcing the
output to logic 1.
The circuit (b) in the ﬁgure 4.6 shows a 2-input CMOS NOR gate where the TN1 and TP1 have the
same input A and TN2 and TP2 has the same input B. When both the A and B are logic 0, TN1 and
TN2 are OFF and TP1 and TP2 are ON. Therefore, the output is at logic 1. On the other hand, when
at least one of the inputs A or B is logic 1, the corresponding nMOS transistor would be ON making
the output logic 0. The output is disconnected from VCC in such case because at least one of the
TP1 or TP2 is OFF. Thus the CMOS circuit acts as a NOR Gate.

4.4. EMITTER COUPLED LOGIC(ECL) 19
Figure 4.6: CMOS NAND and NOR circuit
If one use a CMOS IC for reduced current consumption and a TTL IC feeds the CMOS chip,
then you need to either provide a voltage translation or use one of the mixed CMOS/TTL devices.
The mixed TTL/CMOS devices are CMOS devices, which just happen to have TTL input trigger
levels, but they are CMOS IC’s. Let us consider the TTL to CMOS interface briefly. TTL device
need a supply voltage of 5 V, while CMOS devices can use any supply voltage from 3V to 10V. One
approach to TTL/CMOS interfacing is to use a 5V supply for both the TTL driver and the CMOS
load. In this case, the worst case TTL output voltages are almost compatible with the worst case
CMOS input voltages. There is no problem with the TTL low state window(0 to 0.35 V) because it
fits inside the CMOS low state window(0 to 1.3 V). This means the CMOS load always interprets
the TTL low state drive as low.
4.4 Emitter Coupled Logic(ECL)
Emitter coupled logic(ECL) gates use differential amplifier configurations at the input stage. ECL
is a non saturated logic, which means that transistors are prevented from going into deep sat-
uration, thus eliminating storage delays. In other words, the transistor is switched ON, but not
completely ON. This is the fastest logic family. ECL circuits operate using a negative 5.2V supply
and the voltage level for high is -0.9V and for low is -1.7V. Thus biggest problem with ECL is a poor
noise margin.
4.5 Characteristics of logic families
The parameters which are used to characterize different logic families are as follows:
1. HIGH-level input current(II H ): This is the current flowing into (taken as positive) or out
of (taken as negative) an input, when a HIGH-level input voltage equal to the minimum
HIGH-level output voltage specified for the family is applied. In the case of bipolar logic
families such as TTL, the circuit design is such that this current flows into the input pin and is
therefore specified as positive. In the case of CMOS logic families, it could be either positive
or negative, and only an absolute value is specified in this case. /item LOW-level input
current(IIL): The LOW-level input current is the maximum current flowing into (taken as
positive) or out of (taken as negative) the input of a logic function, when the voltage applied
at the input equals the maximum LOW-level output voltage specified for the family. In the
case of bipolar logic families such as TTL, the circuit design is such that this current flows out

of the input pin and is therefore specified as negative. In the case of CMOS logic families, it
could be either positive or negative. In this case, only an absolute value is specified.
2. HIGH-level output current(IOH ): This is the maximum current flowing out of an output
when the input conditions are such that the output is in the logic HIGH state. It is normally
shown as a negative number. It informs us about the current sourcing capability of the out-
put. The magnitude of IOH determines the number of inputs the logic function can drive
when its output is in the logic HIGH state.
3. LOW-level output current(IOL): This is the maximum current flowing into the output pin
of a logic function when the input conditions are such that the output is in the logic LOW
state. It informs us about the current sinking capability of the output. The magnitude of IOL
determines the number of inputs the logic function can drive when its output is in the logic
LOW state.
4. HIGH-level input voltage(VI H ): This is the minimum voltage level that needs to be applied
at the input to be recognized as a legal HIGH level for the specified family. For the standard
TTL family, a 2V input voltage is a legal HIGH logic state.
5. LOW-level input voltage(VIL): This is the maximum voltage level applied at the input that
is recognized as a legal LOW level for the specified family. For the standard TTL family, an
input voltage of 0.8 V is a legal LOW logic state.
6. HIGH-level output voltage(VOH ): This is the minimum voltage on the output pin of a logic
function when the input conditions establish logic HIGH at the output for the specified fam-
ily. In the case of the standard TTL family of devices, the HIGH level output voltage can be
as low as 2.4V and still be treated as a legal HIGH logic state. It may be mentioned here that,
for a given logic family, the VOH specification is always greater than the VI H specification
to ensure output-to-input compatibility when the output of one device feeds the input of
another.
7. LOW-level output voltage(VOL): This is the maximum voltage on the output pin of a logic
function when the input conditions establish logic LOW at the output for the specified fam-
ily. In the case of the standard TTL family of devices,the LOW-level output voltage can be as
high as 0.4V and still be treated as a legal LOW logic state.It may be mentioned here that,for a
given logic family, the VOLspecification is always smaller than the VIL specification to ensure
output-to-input compatibility when the output of one device feeds the input of another.
8. Fan out: It specifies the number of standard loads that the output of the gate can drive
without affecting its normal operation. A standard load is usually defined as the amount of
current needed by an input of another gate in the same family. Sometimes, the term loading
is also used instead of fan-out. This term is derived from the fact that the output of the gate
can supply a limited amount of current above which it ceases to operate properly and is said
to be overloaded. The output of the gate is usually connected to the inputs of similar gates.
Each input consumes a certain amount of power from gate input so that, each additional
connection adds to load the gate. These loading rules are listed for family of standard digital
circuits. The rules specify the maximum amount of loading allowed for each output in the
circuit.
9. Fan in: This is the number of inputs of a logic gate. It is decided by the input current sinking
capability of a logic gate.

4.5. CHARACTERISTICS OF LOGIC FAMILIES 21
10. Power Dissipation: This is the power supplied required to operate the gate. It is expressed
in milli-watt(mW) and represents actual power dissipated in the gate. It is the number that
represents power delivered to gate from the power supply. The total power dissipated in the
digital system is sum of power dissipated in each digital IC.
11. Propagation delay(tP ): The propagation delay is the time delay between the occurrence of
change in the logical level at the input and before it is reflected at the output. It is the time
delay between the specified voltage points on the input and output wave forms. Propaga-
tion delays are separately defined for LOW-to-HIGH and HIGH-to-LOW transitions at the
output. In addition, we also define enable and disable time delays that occur during transi-
tion between the high-impedance state and defined logic LOW or HIGH states. Propagation
delay is expressed in nanoseconds. The signals travelling from input to output of the sys-
tem pass through a number of gates. The propagation delay of the system is the sum of the
propagation delays of all these gates. The speed of operation is important so each gate must
have a small propagation delay and the digital circuit must have minimum number of gates
between input and output.
Figure 4.7: Propagation delay
Propagation delay parameters
(a) Propagation delay(tpLH ): This is the time delay between the specified voltage points
on the input and output waveforms with the output changing from LOW to HIGH.
(b) Propagation delay (tpHL): This is the time delay between the specified voltage points
on the input and output waveforms with the output changing from HIGH to LOW.
12. Noise margin: This is the maximum noise voltage added to the input signal of digital circuit
that does not cause an undesirable change in the circuit output. There are two types of noise
to be considered here.
• DC noise: This is caused by a drift in the voltage levels of a signal.
• AC noise: This is caused by random pulse that may be created by other switching sig-
nals.

Figure 4.8: Noise margin
Noise margin is a quantitative measure of noise immunity offered by the logic family. When
the output of a logic device feeds the input of another device of the same family, a legal HIGH
logic state at the output of the feeding device should be treated as a legal HIGH logic state
by the input of the device being fed. Similarly, a legal LOW logic state of the feeding de-
vice should be treated as a legal LOW logic state by the device being fed. The legal HIGH and
LOW voltage levels for a given logic family are different for outputs and inputs. The Figure 4.8
shows the generalized case of legal HIGH and LOW voltage levels for output. As we can see
from the two diagrams, there is a disallowed range of output voltage levels from VOL(max)
to VOH (min) and an indeterminate range of input voltage levels from VIL(max) to VI H (min).
Since VIL(max) is greater than VOL(max), the LOW output state can tolerate a positive volt-
age spike equal to (VIL(max)-VOL(max)) and still be a legal LOW input. Similarly, VOH (min)
is greater than VI H (min), and the HIGH output state can tolerate a negative voltage spike
equal to (VOH (min) – VI H (min)) and still be a legal HIGH input. Here,(VIL(max)-VOL(max))
and (VOH (min)-VI H (min)) are respectively known as the LOW-level and HIGH-level noise
margin.
13. Cost: The last consideration, and often the most important one, is the cost of a given logic
family. The ﬁrst approximate cost comparison can be obtained by pricing a common func-
tion such as a dual four-input or quad two-input gate. But the cost of a few types of gates
alone can not indicate the cost of the total system. The total system cost is decided not only
by the cost of ICs but also by the cost of printed wiring board on which the ICs are mounted,
assembly of circuit board, testing, programming the programmable devices, power supply,
documentation, procurement, storage etc. In many instances, the cost of ICs could become
a less important component of the total cost of the system.
4.6 Three State Outputs
Standard logic gate outputs only have two states; high and low. Outputs are effectively either con-
nected to +V or ground, that means there is always a low impedance path to the supply rails. Cer-
tain applications require a logic output that we can "turn off" or disable. It means that the output
is disconnected (high impedance state). This is the three-state output and can be implemented
by a stand-alone unit(a buffer) or part of another function output. This circuit is so-called tri-state
because it has three output states: high(1), low(0) and high impedance(Z).

4.7. OPEN COLLECTOR(DRAIN)OUTPUTS 23
Figure 4.9: Three-state output logic circuit
In the logic circuit of Figure 4.9, there is an additional switch to a digital buffer which is called
as enabled input denoted by E. When E is low, the output is disconnected from the input circuit.
When E is high, the switch is connected and the circuit behaves like a digital buffer. All these states
are listed in truth table and depicts the symbol of a tri-state buffer as shown in the Figure 4.10.
Figure 4.10: Tri-state buffer
4.7 Open Collector(Drain)Outputs
An open collector/open drain is a common type of output found on many integrated circuits. In-
stead of outputting a signal of a specific voltage or current, the output signal is applied to the base
of an internal NPN transistor whose collector is externalized(open) on a pin of the IC. The emit-
ter of the transistor is connected internally to the ground pin. If the output device is a MOSFET,
the output is called open drain and it functions in a similar way. A simple schematic of an open
collector of an IC is as shown in the Figure 4.11.
Figure 4.11: Open collector output circuit of an IC
Open-drain devices sink(flow) current in their low voltage active(logic 0) state, or are high
impedance(no current flows) in their high voltage non-active(logic 1) state. These devices usu-
ally operate with an external pull-up resistor that holds the signal line high until a device on the
wire sinks enough current to pull the line low. Many devices can be attached to the signal wire. If
all devices attached to the wire are in their non-active state, the pull-up will hold the wire at a high
voltage. If one or more devices are in the active state, the signal wire voltage will be low.

An open-collector/open-drain signal wire can also be bi-directional. Bi-directional means
that a device can both output and input a signal on the wire at the same time. In addition to
controlling the state of its pin that is connected to the signal wire(active, or non-active), a device
can also sense the voltage level of the signal wire. Although the output of a open-collector/open-
drain device may be in the non-active(high) state, the wire attached to the device may be in the
active(low) state, due to activity of another device attached to the wire. The open-drain output
configuration turns off all pull-ups and only drives the pull-down transistor of the port pin when
the port latch contains logic ’0’. To be used as a logic output, a port configured in this manner must
have an external pull-up, typically a resistor tied to VDD. The pull down for this mode is the same
as for the quasi-bidirectional mode. To use an analogue input pin as a high-impedance digital
input while a comparator is enabled, that pin should be configured in open-drain mode and the
corresponding port register bit should be set to 1.

Chapter 5
Logic Functions
In electronics, a logic gate is an idealized or physical device implementing a Boolean function, i.e.
it performs a logical operation on one or more binary inputs and produces a single binary output.
A logic gate is an elementary building block of a digital circuit. Most logic gates have two inputs
and one output. At any given moment, every terminal is in one of the two binary conditions low(0)
or high(1), represented by different voltage levels. The logic state of a terminal can, and generally
does, change often, as the circuit processes data. In most logic gates, the low state is approximately
zero volts(0V), while the high state is approximately ﬁve volts positive(+5V). There are seven basic
logic gates: AND, OR, XOR, NOT, NAND, NOR, and XNOR.
AND gate: The AND gate is so named because, if 0 is called "false" and 1 is called "true," the gate
acts in the same way as the logical "and" operator. The Figure 5.1 shows the circuit symbol and
logic combinations for an AND gate. In the symbol, the input terminals are at left and the output
terminal is at right. The output is "true" when both inputs are "true." Otherwise, the output is
"false."
Figure 5.1: AND gate symbol and truth table
OR gate: The OR gate gets its name from the fact that it behaves similar to the logical inclusive
"or." The output is "true" if either or both of the inputs are "true." If both inputs are "false," then
the output is "false."
25

26 CHAPTER 5. LOGIC FUNCTIONS
Figure 5.2: OR gate symbol and truth table
XOR gate: The XOR(exclusive-OR) gate acts in the same way as the logical "either/or." The output
is "true" if either, but not both, of the inputs are "true." The output is "false" if both inputs are
"false" or if both inputs are "true". Another way of looking at this circuit is to observe that the
output is 1 if the inputs are different, but 0 if the inputs are the same.
Figure 5.3: XOR gate symbol and truth table
NOT gate: A logical inverter, sometimes called a NOT gate to differentiate it from other types of
electronic inverter devices, has only one input. It reverses the logic state.
Figure 5.4: NOT gate symbol and truth table
NAND gate: The NAND gate operates as an AND gate followed by a NOT gate. It acts in the
manner of the logical operation "and" followed by negation. The output is "false" if both inputs
are "true". Otherwise, the output is "true".

27
Figure 5.5: NAND gate symbol and truth table
NOR gate: The NOR gate is a combination of OR gate followed by an inverter. Its output is "true"
if both inputs are "false". Otherwise, the output is "false".
Figure 5.6: NOR gate symbol and truth table
XNOR gate: The XNOR(exclusive-NOR) gate is a combination of XOR gate followed by an in-
verter. Its output is "true" if the inputs are the same, and “false" if the inputs are different.
Figure 5.7: XNOR gate symbol and truth table
Using combinations of logic gates, complex operations can be performed. In theory, there is
no limit to the number of gates that can be arrayed together in a single device. But in practice,
there is a limit to the number of gates that can be packed into a given physical space. Arrays of
logic gates are found in digital integrated circuits(ICs). As IC technology advances, the required
physical volume for each individual logic gate decreases and digital devices of the same or smaller
size become capable of performing ever-more-complicated operations at ever-increasing speeds.

Another type of mathematical identity, called a property or a law, describes how differing vari-
ables relate to each other in a system of numbers. One of these properties is known as the commu-
tative property, and it applies equally to addition and multiplication. In essence, the commutative
property tells us we can reverse the order of variables that are either added together or multiplied
together without changing the truth of the expression.
Figure 5.8: Commutative property of addition
Figure 5.9: Commutative property of multiplication
Along with the commutative property of addition and multiplication, we have the associative
property, again applying equally well to addition and multiplication. This property tells us we can
associate groups of added or multiplied variables together with parentheses without altering the
truth of the equations.
Figure 5.10: Associative property of addition

5.1. TRUTH TABLE DESCRIPTION OF LOGIC FUNCTIONS 29
Figure 5.11: Associative property of multiplication
Lastly, we have the distributive property, illustrating how to expand a Boolean expression formed
by the product of a sum, and in reverse shows us how terms may be factored out of Boolean sums-
of-products.
Figure 5.12: Distributive property
5.1 Truth Table Description of Logic Functions
The truth table is a tabular representation of a logic function. It gives the value of the function for
all possible combinations of values of the variables. If there are three variables in a given function,
there are 23
= 8 combinations of these variables. For each combination, the function takes either
1 or 0. These combinations are listed in a table, which constitutes the truth table for the given
function. Consider the expression,
F(A,B) = A.B + A. ¯B (5.1)
The truth table for this function is given by
Figure 5.13: Truth table for the expression 5.1

The information contained in the truth table and in the algebraic representation of the function
are the same. The term truth table came into usage long before Boolean algebra came to be associ-
ated with digital electronics. Boolean function were originally used to establish truth or falsehood
of statements. When statement is true the symbol "1" is associated with it, and when it is false "0" is
associated. This usage got extended to the variables associated with digital circuits. However, this
usage of adjectives "true" and "false" is not appropriate when associated with variables encoun-
tered in digital systems. All variables in digital systems are indicative of actions. Typical examples
of such signals are "CLEAR", "LOAD", "SHIFT", "ENABLE" and "COUNT". These are suggestive of
actions. Therefore, it is appropriate to state that a variable is ASSERTED or NOT ASSERTED than to
say that a variable is TRUE or FALSE. When a variable is asserted, the intended action takes place,
and when it is not asserted the intended action does not take place. In this context, we associate
"1" with the assertion of a variable and "0" with the non-assertion of that variable. Consider the
logic function,
F(A,B) = A.B + A. ¯B (5.2)
It should now be read as, F is asserted when A and B are asserted or A is asserted and B is not
asserted. This convention of using assertion and non-assertion with the logic variables will be
used in all the learning units of digital systems. The term truth table will continue to be used for
historical reasons. But we understand it as an input-output table associated with a logic function,
but not as something that is concerned with the establishment of truth.
As the number of variables in a given function increases, the number of entries in the truth
table increases exponentially. For example, a ﬁve variable expression would require 32 entries and
a six-variable function would require 64 entries. Therefore, it becomes inconvenient to prepare
the truth table if the number of variables increases beyond four. However, a simple artefact may
be adopted. A truth table can have entries only for those terms for which the value of the function
is "1", without loss of any information. This is particularly effective when the function has only a
small number of terms. Consider the Boolean function with six variables.
F = A.B.C. ¯D. ¯E + A. ¯B.C. ¯D.E + ¯A. ¯B.C.D.E + A. ¯B. ¯C.D.E (5.3)
The truth table will have only four entries rather than 64 and the representation of this function is
as shown in the Figure 5.14.
Figure 5.14: Truth table for the expression 5.3
Truth table is a very effective tool in working with digital circuits, especially when the number of
variables in a function is small, less than or equal to ﬁve.

5.2. CONVERSION OF ENGLISH SENTENCES TO LOGIC FUNCTIONS: 31
5.2 Conversion of English Sentences to Logic Functions:
Some of the problems that can be solved using digital circuits are expressed through one or more
sentences.
For example, consider the sentence "Lift starts moving only if doors are closed and button is
pressed".
Break the sentence into phrases
F = lift starts moving(1) or else(0)
A = doors are closed(1) or else(0)
B = floor button is pressed(1) or else(0)
So F = (A,B)
In complex causes, we need to define variable properly and drawn truth table before logic func-
tion can be written as an expression. There may be some vagueness that should be defined.
For example, "’A’ will go for a workshop if and only if ’B’ is going and the subject of workshop is
important from career perspective or if the venue is interesting and there is no academic com-
mitment".
F = A.B +C ¯D (5.4)
5.3 Boolean Function Representation
The use of switching devices like transistors give rise to a special case of the Boolean algebra called
as switching algebra. In switching algebra, all the variables assume one of the two values which
are 0 and 1. In Boolean algebra, 0 is used to represent the ‘open’ state or ‘false’ state of logic gate.
Similarly, 1 is used to represent the ‘closed’ state or true state of logic gate.
A Boolean expression is an expression which consists of variables, constants(0-false and 1-true)
and logical operators which results in true or false. A Boolean function is an algebraic form of
Boolean expression. A Boolean function of n−variables is represented by f (X1,X2,X3,..., Xn). By
using Boolean laws and theorems, we can simplify the Boolean functions of digital circuits. A brief
note of different ways of representing a Boolean function are as follows:
• Sum-of-Products(SOP) form
• Product-of-sums(POS) form
• Canonical and standard forms
5.3.1 Some Definitions of Logic Functions
1. Literal: A variable or its complement i.e A or ¯A.
2. Product term: A term with the product(Boolean multiplication) of literals.
3. Sum term: A term with the sum(Boolean addition) of literals.
The min-terms and max-terms may be used to define the two standard forms for logic expres-
sions, namely the sum of products (SOP) or sum of min-terms and the product of sums(POS) or
product of max-terms. These standard forms of expression aid the logic circuit designer by sim-
plifying the derivation of the function to be implemented. Boolean functions expressed as a sum
of products or a product of sums are said to be in canonical form. Note the POS is not the comple-
ment of the SOP expression.

5.3.2 Sum of Product (SOP) Form
The sum-of-products form is a method(or form) of simplifying the Boolean expressions of logic
gates. In this SOP form of Boolean function representation, the variables are operated by AND
(product) to form a product term and all these product terms are ORed(summed or added) to-
gether to get the final function. A sum-of-products form can be formed by adding(or summing)
two or more product terms using a Boolean addition operation. Here the product terms are de-
fined by using the AND operation and the sum term is defined by using OR operation. The sum-of-
products form is also called as Disjunctive Normal Form as the product terms are ORed together
and disjunction operation is logical OR. Sum-of-products form is also called as Standard SOP.
5.3.3 Product of Sums(POS) Form
The product of sums form is a method(or form) of simplifying the Boolean expressions of logic
gates. In this POS form, all the variables are ORed i.e. written as sums to form sum terms. All these
sum terms are ANDed (multiplied) together to get the product-of-sum form. This form is exactly
opposite to the SOP form. So this can also be said as dual of SOP form. Here the sum terms are
defined by using the OR operation and the product term is defined by using AND operation. When
two or more sum terms are multiplied by a Boolean OR operation, the resultant output expression
will be in the form of product-of-sums form or POS form. The product-of-sums form is also called
as Conjunctive Normal Form as the sum terms are ANDed together and conjunction operation is
logical AND. Product-of-sums form is also called as Standard POS.
Example: Consider the truth table for half adder shown in the figure 5.15.
Figure 5.15: Truth table of half adder
The sum-of-products form is obtained as
S = ( ¯A.B)+(A. ¯B)
C = (A.B)
The product-of-sums form is obtained as
S = (A +B).( ¯A + ¯B)
C = (A +B).(A + ¯B).( ¯A +B)
Figure 5.16: Circuit diagram for the example in Figure 5.15

5.4. SIMPLIFICATION OF LOGIC FUNCTIONS 33
5.4 Simplification of Logic Functions
• Logic expression may be long with many terms with many literals.
• Can be simplified using Boolean algebra.
• Simplification requires ability to identity patterns.
• If we can represent logic function in a graphic form that helps us in identifying patterns,
simplification becomes simple.
5.5 Karnaugh Map(or K-map) minimization
The Karnaugh map provides a systematic method for simplifying a Boolean expression or a truth
table function. The K map can produce the simplest SOP or POS expression possible. K-map
procedure is actually an application of adjacency and guarantees a minimal expression. It is easy
to use, visual, fast and familiarity with Boolean laws is not required. The K-map is a table consisting
of N = 2n
cells, where n is the number of input variables. Assuming the input variables are A and
B, then the K-map illustrating the four possible variable combinations is obtained.
Let us begin by considering a two-variable logic function
F = ¯AB + AB
Any two-variable function has 22
= 4 min-terms. The truth table of this function is as shown in the
Figure 5.17.
Figure 5.17: Truth table
It can be seen that the values of the variables are arranged in the ascending order(in the numerical
decimal sense).
Figure 5.18: Two variable K-map
Example: Consider the expression Z = f (A,B) = ¯A. ¯B+A. ¯B+ ¯A.B plotted on the k-map as shown
in the Figure 5.19.

Figure 5.19: K-map
Pairs of 1’s are grouped as shown in the Figure 5.19 and the simplified answer is obtained by using
the following steps:
• Note that two groups can be formed for the example given above, bearing in mind that the
largest rectangular clusters that can be made consist of two 1’s. Notice that a 1 can belong to
more than one group.
• The first group labelled I, consists of two 1’s which correspond to A = 0, B = 0 and A = 1,
B = 0. Put in another way, all squares in this example that correspond to the area of the map
where B = 0 contains 1’s, independent of the value of A. So when B = 0, the output is 1. The
expression of the output will contain the term ¯B.
• For group labelled I I corresponds to the area of the map where A = 0. The group can there-
fore be defined as ¯A. This implies that when A = 0, the output is 1. The output is therefore 1
whenever B = 0 and A = 0.
Hence, the simplified answer is Z = ¯A + ¯B.
5.5.1 Three Variable and Four Variable Karnaugh Map:
The three variable and four variable K-maps can be constructed as shown in the Figure 5.20.
Figure 5.20: Three and four variable K-map
K-map for three variables will have 23
= 8 cells and for three variables will have 24
= 16 cells.
It can be observed that the positions of columns 10 and 11 are interchanged so that there is only
change in one variable across adjacent cells. This modification will allow in minimizing the logic.
Example: 3-variable K-Map for the function, F = (1,2,3,4,5,6)
Figure 5.21: Three variable K-map for the given expression
Simplified expression from the K-map is F = ¯A.C +B. ¯C + A. ¯B.
Example: Consider the function, F = (0,1,3,5,6,9,11,12,13,15)
Since, the biggest number is 15, we need to have 4 variables to define this function. The K-Map for
this function is obtained by writing 1 in cells that are present in function and 0 in rest of the cells.

5.5. KARNAUGH MAP(OR K-MAP) MINIMIZATION 35
Figure 5.22: Four variable K-map for the given expression
Simplified expression obtained : F = ¯C.D + AD + ¯A. ¯B. ¯C + ¯A. ¯B. ¯D + AB ¯C + ¯ABC ¯D.
Example: Given function, F = sum(0,2,3,4,5,7,8,9,13,15)
Figure 5.23: K-map for the given expression
Simplified expression obtained: F = B.D + ¯A. ¯C. ¯D + ¯A. ¯B.C + A. ¯B. ¯C.
5.5.2 Five Variable K-Map:
A 5-variable K-Map will have 25
= 32 cells. A function F which has maximum decimal value of 31,
can be defined and simplified by a 5-variable Karnaugh Map.
Figure 5.24: Five variable K-map
Example 5: Given function, F = (1,3,4,5,11,12,14,16,20,21,30)
Since, the biggest number is 30, we need to have 5 variables to define this function. K-map for the
function is as shown in the Figure 5.25
Figure 5.25: Five variable K-map for example 5
Simplified expression: F = ¯B.C. ¯D + ¯A.B.C ¯E +B.C.D. ¯E + ¯A. ¯C.D.E + A ¯B. ¯D. ¯E + ¯A. ¯B. ¯C.E
Example 6: Given function, F = (0,1,2,3,8,9,16,17,20,21,24,25,28,29,30,31)

Figure 5.26: Five variable K-map for example 6
Simpliﬁed expression:F = A. ¯D + ¯C. ¯D + ¯A. ¯B. ¯C + A.B.C
5.5.3 Implementation of BCD to Gray code Converter using K-map
We can convert the Binary Coded Decimal(BCD) code to Gray code by using K-map simpliﬁcation.
The truth table for BCD to Gray code converter is shown in the Figure 5.27
Figure 5.27: Table for BCD to Gray code converter
Figure 5.28: K-map for G3 and G2
Figure 5.29: K-map for G1 and G0
The equations obtained from K-maps are as follows:
G3 = B3

5.6. MINIMIZATION USING K-MAP 37
G2 = ¯B3.B2+B3. ¯B2 = B3⊕B2
G1 = ¯B1.B2+B1. ¯B2 = B1⊕B2
G0 = ¯B1.B0+B1. ¯B0 = B1⊕B0
The implementation of BCD to Gray conversion using logic gates is shown in the Figure 5.30.
Figure 5.30: Binary to Gray code converter circuit
5.6 Minimization using K-map
Some deﬁnitions used in minimization:
• Implicant: An implicant is a group of 2i
(i = 0,1,...,n) minterms (1-entered cells) that are
logically adjacent.
• Prime implicant: A prime implicant is the one that is not a subset of any one of other impli-
cant.
A study of implicants enables us to use the K-map effectively for simplifying a Boolean func-
tion. Consider the K-map shown in the Figure 5.31. There are four implicants: 1, 2, 3 and
4.
Figure 5.31: K-map showing implicants and prime implicants
The implicant 4 is a single cell implicant. A single cell implicant is a 1-entered cell that is not
positionally adjacent to any of the other cells in the map. The four implicants account for all
groupings of 1-entered cells. This also means that the four implicants describe the Boolean
function completely. An implicant represents a product term, with the number of variables
appearing in the term inversely proportional to the number of 1-entered cells it represents.
Implicant 1 in the Figure 5.31 represents the product term A. ¯C.
Implicant 2 represents A.B.D.
Implicant 3 represents B.C.D.
Implicant 4 represents ¯A. ¯B.C. ¯D.
The smaller the number of implicants, and the larger the number of cells that each implicant
represents, the smaller the number of product terms in the simpliﬁed Boolean expression.
• Essential prime implicant: It is a prime implicant which includes a 1-entered cell that is not
include in any other prime implicant.
• Redundant implicant: It is the one in which all cells are covered by other implicants. A
redundant implicant represents a redundant term in an expression.

5.6.1 K-maps for Product-of-Sum Design
Product-of-sums design uses the same principles, but applied to the zeros of the function.
Example 7: F = π(0,4,6,7,11,12,14,15)
In constructing the K-map for the function given in POS form, 0’s are filled in the cells represented
by the max terms. The K-map of the above function is shown in the Figure 5.32.
Figure 5.32: K-map for the example 7
Sometimes the function may be given in the standard POS form. In such situations, we can initially
convert the standard POS form of the expression into its canonical form, and enter 0’s in the cells
representing the max terms. Another procedure is to enter 0’s directly into the map by observing
the sum terms one after the other. Consider an example of a Boolean function given in the POS
form.
F = (A +B + ¯D).( ¯A +B + ¯C).( ¯B +C)
This may be converted into its canonical form as follows:
F = (A+B +C + ¯D).(A+B + ¯C + ¯D).( ¯A+B + ¯C +D).(A+ ¯B +C +D).( ¯A+ ¯B +C + ¯D).(A+ ¯B +C + ¯D).( ¯A+
¯B +C + ¯D)
F = M1.M3.M10.M4.M12.M5.M13
The cells 1, 3, 4, 5, 10, 12 and 13 have 0’s entered in them while the remaining cells are filled with
1’s.
5.6.2 DON’T CARE CONDITIONS
Functions that have unspecified output for some input combinations are called incompletely spec-
ified functions. Unspecified min-terms of a functions are called don’t care conditions. We simply
don’t care whether the value of 0 or 1 is assigned to F for a particular min term. Don’t care con-
ditions are represented by X in the K-Map table. Don’t care conditions play a central role in the
specification and optimization of logic circuits as they represent the degrees of freedom of trans-
forming a network into a functionally equivalent one.
Example 8: Simplify the Boolean function
f (w,x, y,z) = S(1,3,7,11,15), d(w,x, y,z) = S(0,2,5)

5.6. MINIMIZATION USING K-MAP 39
The function in the SOP and POS forms may be written as
F = (4,5)+d(0,6,7) and F = π(1,2,3).d(0,6,7)
The term d(0,6,7) represents the collection of don’t-care terms. The don’t-cares bring some ad-
vantages to the simplification of Boolean functions. The X ’s can be treated either as 0’s or as 1’s
depending on the convenience. For example the above K-map shown in the Figure 5.33 can be
redrawn in two different ways as shown in the Figure 5.34.
Figure 5.34: Different ways of K-map for the example 8
The simplification can be done in two different ways. The resulting expressions for the function F
are: F = A and F = A ¯B
Therefore, we can generate a simpler expression for a given function by utilizing some of the don’t-
care conditions as 1’s.
Example 9: Simplify F = (0,1,4,8,10,11,12)+d(2,3,6,9,15) The K-map of this function is shown
in the Figure 5.35.
The simplified expression taking the full advantage of the don’t cares is F = ¯B + ¯C. ¯D
Simplification of Several Functions of the Same Set of Variables: As there could be several prod-
uct terms that could be made common to more than one function, special attention needs to be
paid to the simplification process.
Example 10: Consider the following set of functions defined on the same set of variables:
F1(A,B,C) = (0,3,4,5,6)
F2(A,B,C) = (1,2,4,6,7)

F3(A,B,C) = (1,3,4,5,6)
Let us first consider the simplification process independently for each of the functions. The K-
maps for the three functions and the groupings are shown in the Figure 5.36.
The resultant minimal expressions are:
F1 = ¯B. ¯C + A. ¯C + A. ¯B + ¯A.B.C
F2 = B. ¯C + A. ¯C + A.B + ¯A. ¯B.C
F3 = A. ¯C + ¯B.C + ¯A.C
These three functions have nine product terms and twenty one literals. If the groupings can be
done to increase the number of product terms that can be shared among the three functions, a
more cost effective realization of these functions can be achieved. One may consider, at least as
a first approximation, cost of realizing a function is proportional to the number of product terms
and the total number of literals present in the expression. Consider the minimization shown in the
Figure 5.37.
The resultant minimal expressions are:
F1 = ¯B. ¯C + A. ¯C + A. ¯B + ¯A.B.C
F2 = B. ¯C + A. ¯C + A.B + ¯A. ¯B.C
F3 = A. ¯C + A. ¯B + ¯A.B.C + ¯A. ¯B.C
This simplification leads to seven product terms and sixteen literals.
5.7 Quine-McCluskey Method of Minimization
Karnaugh Map provides a good method of minimizing a logic function. However, it depends on
our ability to observe appropriate patterns and identify the necessary implicants. If the number of
variables increases beyond five, K-map or its variant variable entered map can become very messy
and there is every possibility of committing a mistake. What we require is a method that is more
suitable for implementation on a computer, even if it is inconvenient for paper-and-pencil pro-
cedures. The concept of tabular minimisation was originally formulated by Quine in 1952. This
method was later improved upon by McClusky in 1956, hence the name Quine-McClusky
This learning unit is concerned with the Quine-McClusky method of minimisation. This method
is tedious, time-consuming and subject to error when performed by hand. But it is better suited
to implementation on a digital computer.

5.7. QUINE-MCCLUSKEY METHOD OF MINIMIZATION 41
5.7.1 Principle of Quine-McClusky Method
Generate prime implicants of the given Boolean function by a special tabulation process. Deter-
mine the minimal set of implicants is determined from the set of implicants generated in the first
stage. The tabulation process starts with a listing of the specified minterms for the 1’s (or 0’s) of a
function and don’t-cares (the unspecified minterms) in a particular format. All the prime impli-
cants are generated from them using the simple logical adjacency theorem, namely, A ¯B + AB = A.
The main feature of this stage is that we work with the equivalent binary number of the product
terms.
For example in a four variable case, the minterms ¯ABC ¯D and ¯AB ¯C ¯D are entered as 0110 and 0100.
As the two logically adjacent ¯ABC ¯D and ¯AB ¯C ¯D can be combined to form a product term ¯AB ¯D the
two binary terms 0110 and 0100 are combined to form a term represented as 01−0, where ‘-‘(dash)
indicates the position where the combination took place.
Stage two involves creating a prime implicant table. This table provides a means of identifying, by
a special procedure, the smallest number of prime implicants that represents the original Boolean
function. The selected prime implicants are combined to form the simplified expression in the
SOP form. While we confine our discussion to the creation of minimal SOP expression of a Boolean
function in the canonical form, it is easy to extend the procedure to functions that are given in the
standard or any other forms
5.7.2 Generation of Prime Implicants
The process of generating prime implicants is best presented through an example.
Example 10: F = (1,2,5,6,7,9,10,11,14)
All the minterms are tabulated as binary numbers in sectionalised format, so that each section
consists of the equivalent binary numbers containing the same number of 1’s, and the number
of 1’s in the equivalent binary numbers of each section is always more than that in its previous
section. This process is illustrated in the table as shown in the Figure 5.38.
Figure 5.38: Table for example 10
The next step is to look for all possible combinations between the equivalent binary numbers in
the adjacent sections by comparing every binary number in each section with every binary num-
ber in the next section. The combination of two terms in the adjacent sections is possible only if
the two numbers differ from each other with respect to only one bit. For example 0001(1) in section
1 can be combined with 0101(5) in section 2 to result in 0−01(1,5). Notice that combinations can-
not occur among the numbers belonging to the same section. The results of such combinations
are entered into another column, sequentially along with their decimal equivalents indicating the
binary equivalents from which the result of combination came, like (1,5) as mentioned above. The

second column also will get sectionalised based on the number of 1’s. The entries of one section
in the second column can again be combined together with entries in the next section in a similar
manner. These combinations are illustrated in the table shown in the Figure 5.39.
All the entries in the column which are paired with entries in the next section are checked off.
Column 2 is again sectionalised with respect to the number of 1’s. Column 3 is generated by pairing
off entries in the ﬁrst section of the column 2 with those items in the second section. In principle,
this pairing could continue until no further combinations can take place. All those entries that are
paired can be checked off. It may be noted that combination of entries in column 2 can only take
place if the corresponding entries have the dashes at the same place. This rule is applicable for
generating all other columns as well. After the tabulation is completed, all those terms which are
not checked off constitute the set of prime implicants of the given function. The repeated terms,
like −−10 in the column 3, should be eliminated. Therefore, from the above tabulation procedure,
we obtain seven prime implicants (denoted by their decimal equivalents) as (1,5), (1,9), (5,7), (6,7),
(9,11), (10,11) and (2,6,10,14). The next stage is to determine the minimal set of prime implicants.
5.7.3 Determination of the Minimal Set of Prime Implicants
The prime implicants generated through the tabular method do not constitute the minimal set.
The prime implicants are represented in so called "prime implicant table". Each column in the
table represents a decimal equivalent of the min term. A row is placed for each prime implicant
with its corresponding product appearing to the left and the decimal group to the right side. Aster-
isks are entered at those intersections where the columns of binary equivalents intersect the row
that covers them. The prime implicant table for the function under consideration is shown in the
Figure 5.40.
Figure 5.40: Prime implicant table for example 10

In the selection of minimal set of implicants, similar to that in a K-map, essential implicants should
be determined ﬁrst. An essential prime implicant in a prime implicant table is one that covers (at
least one) minterms which are not covered by any other prime implicant. This can be done by
looking for that column that has only one asterisk. For example, the columns 2 and 14 have only
one asterisk each. The associated row, indicated by the prime implicant C ¯D is an essential prime
implicant. C ¯D is selected as a member of the minimal set (mark that row by an asterisk). The
corresponding columns, namely 2, 6, 10 and 14 are also removed from the prime implicant table,
and a new table is constructed as shown in the Figure 5.41.
We then select dominating prime implicants, which are the rows that have more asterisks than oth-
ers. For example, the row ¯ABD includes the min term 7, which is the only one included in the row
represented by ¯ABC. ¯ABD is dominant implicant over ¯ABC, and hence ¯ABC can be eliminated.
Mark ¯ABD by an asterisk and check off the column 5 and 7. Then choose AB ¯D as the dominating
row over the row represented by A ¯BC. Consequently, we mark the row A ¯BD by an asterisk and
eliminate the row A ¯BC and the columns 9 and 11 by checking them off. Similarly, we select ¯A. ¯C. ¯D
as the dominating one over ¯B ¯C.D. However, ¯B. ¯C.D can also be chosen as the dominating prime
implicant and eliminate the implicant ¯A ¯CD. Retaining A/C/D as the dominant prime implicant
the minimal set of prime implicant are C ¯D, ¯A ¯CD, ¯ABD and A ¯BD. The corresponding minimal
SOP expression for the Boolean function is:
F = C ¯D + ¯A ¯CD + ¯ABD + A ¯BD
This indicates that if the selection of the minimal set of prime implicants is not unique, then the
minimal expression is also not unique.
There are two types of implicant tables that have some special properties. One is referred to as
cyclic prime implicant table and the other as semi-cyclic prime implicant table. A prime impli-
cant table is considered to be cyclic if it does not have any essential implicants which implies that
there are at least two asterisks in every column. There are no dominating implicants, which im-
plies that there are same number of asterisks in every row.
Example 11: A Boolean function with a cyclic prime implicant table is shown in the Figure 5.42.
The function is given by F = (0,1,3,4,7,12,14,15), the possible prime implicant of the functions
are (0,1), (0,4), (1,3), (3,7), (4,12), (7,15), (12,14) and (14,15).

Figure 5.42: Cyclic prime implicant table for example 11
As it may be noticed from the prime implicant table in the Figure 5.43 that all columns have two
asterisks and there are no essential prime implicants. In such a case, we can choose any one of the
prime implicants to start with. If we start with prime implicant a, it can be marked with asterisk
and the corresponding columns for 0 and 1 can be deleted from the table. After their removal, row
c becomes dominant over row b, so that row c is selected and hence row b can be eliminated. The
columns 3 and 7 can now be deleted. We observe then that the row e dominates row d and row d
can be eliminated. Selection of row e enables us to delete columns 14 and 15.
If, from the reduced prime implicant table shown in the Figure 5.43 we choose row g, it covers the
remaining asterisks associated with rows h and f . That covers the entire prime implicant table.
The minimal set for the Boolean function is given by:

F = a +c +e + g
F = ¯A ¯B ¯C + ¯ACD + ABC +B ¯C ¯D
The K-map of the simplified function is shown in the Figure ??.
Figure 5.45: K-map for example 11
A semi-cyclic prime implicant table differs from a cyclic prime implicant table in one respect. In
the cyclic case the number of minterms covered by each prime implicant is identical. In a semi-
cyclic function this is not necessarily true.
5.7.4 Simplification of Incompletely Specified functions
The simplification procedure for completely specified functions presented in the earlier sections
can easily be extended to incompletely specified functions. The initial tabulation is drawn up
including the dont-cares. However, when the prime implicant table is constructed, columns asso-
ciated with don’t-cares need not be included because they do not necessarily have to be covered.
The remaining part of the simplification is similar to that for completely specified functions.
Example 12: Simplify the following function:
F(A,B,C,D,E) = (1,4,6,10,20,22,24,26)+d(0,11,16,27)
We need to pay attention to the don’t-care terms as well as to the combinations among them-
selves, by marking them with (d). Six binary equivalents are obtained from the procedure. These
are 0000−(0,1), 1−000(16,24), 110−0(24,26), −0−00(0,4,16,20), −01−0(4,6,20,22) and −101−
(10,11,26,27) and they correspond to the following prime implicants:
a = ¯A ¯B ¯C ¯D
b = ¯A ¯C ¯D ¯E
c = AB ¯C ¯E
d = ¯B ¯d ¯E
e = ¯BC ¯E
g = B ¯CD
The prime implicant table is plotted as shown in the Figure 5.47.

It may be noted that the don’t-cares are not included.
The minimal expression is given by:
F(A,B,C,D,E) = a +c +e + g
F(A,B,C,D,E) = ¯A ¯B ¯C ¯D + AB ¯C ¯E +B ¯CE +B ¯CD
5.8 Timing Hazards
If the input of a combinational circuit changes, unwanted switching variations may appear in the
output. These variations occur when different paths from the input to output have different delays.
If, from response to a single input change and for some combination of propagation delay, an
output momentarily goes to 0 when it should remain a constant value of 1, the circuit is said to
have a static 1-hazard. Likewise, if the output momentarily goes to 1 when it should remain at a
constant value of 0, the circuit is said to have a 0-hazard. When an output is supposed to change
values from 0 to 1, or 1 to 0, this output may change three or more times. If this situation occurs,
the circuit is said to have a dynamic hazard. The Figure 5.48 shows the different outputs from a
circuit with hazards. In each of the three cases, the steady-state output of the circuit is correct,
however a switching variation appears at the circuit output when the input is changed.
Figure 5.48: Timing hazards
The ﬁrst hazard, the static 1-hazard depicts that if A = C = 1, then F = B + B = 1, thus the
output F should remain at a constant 1 when B changed from 1 to 0. However in the next illus-
tration, the static 0-hazard , if each gate has a propagation of 10ns, E will go to 0 before D goes
to 1, resulting in a momentary 0 appearing at output F. This is also known to be a glitch caused
by the 1-hazard. One should note that right after B changes to 0, both the inverter input(B) and
output(B’) are 0 until the delay has elapsed. During this propagation period, both of these input
terms in the equation for F have value of 0, so F also momentarily goes to a value of 0.
These hazards, static and dynamic, are completely independent of the propagation delays that
exist in the circuit. If a combinational circuit has no hazards, then it is said that for any combina-
tion of propagation delays and for any individual input change, that output will not have a vari-
ation in I/O value. On the contrary, if a circuit were to contain a hazard, then there will be some

5.8. TIMING HAZARDS 47
combination of delays as well as an input change for which the output in the circuit contains a
transient. This combination of delays that produce a glitch may or may not be likely to occur in
the implementation of the circuit. In some instances, it is very unlikely that such delays would
occur. The transients (or glitches) that result from static and dynamic timing hazards very seldom
cause problems in fully synchronous circuits, but they are a major issue in asynchronous circuits
(which includes nominally synchronous circuits that involve either the use of asynchronous pre-
set/reset inputs that use gated clocks).
The variation in input and output also depends on how each gate will respond to a change of input
value. In some instances, if more than one input gate changes within a short amount of time, the
gate may or may not respond to the individual input changes. An example is shown in the Figure
5.49 assuming that the inverter(B) has a propagation delay of 2ns instead of 10ns. Then input D
and E changes reaching the output OR gate are 2ns from each other, thus the OR gate may or may
not generate the 0 glitch.
Figure 5.49: Timing diagram
A gate displaying this type of response is said to have what is known as an inertial delay. Rather of-
ten the inertial delay value is presumed to be the same as the propagation delay of the gate. When
this occurs, the circuit above will respond with a 0 glitch only for inverter propagation delays that
are larger than 10ns. However, if an input gate invariably responds to input change that has a
propagation delay, is said to have an ideal or transport delay. If the OR gate shown above has this
type of delay, then a 0 glitch would be generated for any nonzero value for the inverter propagation
delay.
Hazards can always be discovered using a Karnaugh map. The map illustrated above in Figure
5.49 in which not even a single loop covers both minterms ABC and A ¯BC. Thus if A = C = 1 and
¯Bs value changes, both of these terms can go to 0 momentarily; from this momentary change, a 0
glitch is found in F. To detect hazards in a two-level AND-OR combinational circuit, the following
procedure is completed.
• A sum-of-products expression for the circuit needs to be written out.
• Each term should be plotted on the map and looped, if possible.

• If any two adjacent 1’s are not covered by the same loop, then a 1-hazard exists for the tran-
sition between those two 1’s. For any n variable map, this transition only occurs when one
variable changes value and the other (n − 1) variables are held constant. If another loop is
added to the Karnaugh map in the above Figure 5.49 and then add the corresponding gate
to the circuit in the Figure 5.50, the hazard can be eliminated. The term AC remains at a
constant value of 1 while B is changing, thus a glitch cannot appear in the output. With this
change, F is no longer a minimum SOP.
Figure 5.50: Timing diagram
The Figure 5.51(a) shows a circuit with numerous 0-hazards. The function that represents the cir-
cuit’s output is: F = (A +C)( ¯A + ¯D)( ¯A + ¯C + D). The Karnaugh map in the Figure 5.51(b) has four
pairs of adjacent 0’s that are not covered by a common loop. The arrows indicate where each 0 is
not being looped, and they each correspond to a 0-hazard. If A = 0, B = 1, D = 0 and C changes
from 0 to 1, there is a chance that a spike can appear at the output for any combination of gate de-
lays. Lastly, Figure 5.51(c) depicts a timing diagram that, assumes a delay of 3ns for each individual
inverter and a delay of 5ns for each AND gate and each OR gate.
Figure 5.51: Timing diagram for the circuit

5.8. TIMING HAZARDS 49
The 0-hazards can be eliminated by looping extra prime implicants that cover the 0’s adjacent
to one another, as long as they are not already covered by a common loop. By eliminating alge-
braically redundant terms, or consensus terms, the circuit can be reduced to the following equa-
tion below. Using three additional loops will completely eliminate the 0-hazards, resulting the
following equation.
F = (A +C)( ¯A + ¯D)( ¯B + ¯C +D)(C + ¯D)(A + ¯B +D)( ¯A + ¯B + ¯C)
The Figure 5.52 below illustrates the Karnaugh map after removing the 0-hazards.
Figure 5.52: Timing diagram after removing 0-hazards

Chapter 6
Combinational Circuits
6.1 Decoder
Decoder is a combinational circuit that has ‘n’ input lines and maximum of 2n
output lines. One of
these outputs will be active HIGH based on the combination of inputs present, when the decoder
is enabled. That means decoder detects a particular code. The outputs of the decoder are nothing
but the min terms of ‘n’ input variables (lines), when it is enabled.
6.1.1 2 to 4 Decoder:
Let 2 to 4 decoder has two inputs A1 & A0 and four outputs Y3, Y2, Y1 & Y0. The block diagram of
2 to 4 decoder is shown in the following Figure 6.1.
Figure 6.1: Block diagram of 2 to 4 decoder
One of these four outputs will be 1 for each combination of inputs when enable, E is 1. The Truth
table of 2 to 4 decoder is shown in the Figure 6.2.
Figure 6.2: Truth table of 2 to 4 decoder
51

52 CHAPTER 6. COMBINATIONAL CIRCUITS
Y 3 = E.A1.A0
Y 2 = E.A1. ¯A0
Y 1 = E. ¯A1.A0
Y 0 = E. ¯A1. ¯A0
Each output is having one product term. So, there are four product terms in total. We can im-
plement these four product terms by using four AND gates having three inputs each & two inverts.
The circuit diagram of 2 to 4 decoder is shown in the following Figure 6.3.
Figure 6.3: Circuit diagram of 2 to 4 decoder
Therefore, the outputs of 2 to 4 decoder are nothing but the minterms of two input variables A1 &
A0, when enable, E is equal to one. If enable, E is zero, then all the outputs of decoder will be equal
to zero.
6.1.2 3 to 8 line decoder
This decoder circuit gives 8 logic outputs for 3 inputs and has a enable pin. The circuit is designed
with AND and NAND logic gates. It takes 3 binary inputs and activates one of the eight outputs. 3
to 8 line decoder circuit is also called as binary to an octal decoder.
Figure 6.4: Block diagram of 3 to 8 line decoder
The decoder circuit works only when the Enable pin (E) is high. S0, S1 and S2 are three different
inputs and D0, D1, D2, D3, D4, D5, D6 and D7 are the eight outputs. When the Enable pin (E) is
low all the output pins are low.

6.1. DECODER 53
Figure 6.5: Circuit diagram of 3 to 8 line decoder
Figure 6.6: Truth table of 3 to 8 line decoder
6.1.3 Implementation of higher-order decoders
Higher order decoders can be implemented using one or more lower order decoders.
3 to 8 Decoder: It can be implemented using 2 to 4 decoders. We know that 2 to 4 decoder has
two inputs, A1 & A0 and four outputs, Y3 to Y0. Whereas, 3 to 8 decoder has three inputs A2, A1
& A0 and eight outputs, Y7 to Y0. The number of lower order decoders required for implementing
higher order decoder can be obtained using the following formula.
Required number of lower order decoders = m2/m1
where, m1 is the number of outputs of lower order decoder and m2 is the number of outputs of
higher order decoder.
Here, m1=4 and m2=8. Substituting these two values in the above formula.
Required number of 2 to 4 decoders=8/4=2
Therefore, we require two 2 to 4 decoders for implementing one 3 to 8 decoder. The block diagram
of 3 to 8 decoder using 2 to 4 decoders is shown in the following Figure 6.7.
Figure 6.7: Circuit diagram of 3 to 8 decoder

The parallel inputs A1 & A0 are applied to each 2 to 4 decoder. The complement of input A2 is
connected to Enable, E of lower 2 to 4 decoder in order to get the outputs, Y3 to Y0. These are the
lower four minterms. The input A2 is directly connected to Enable, E of upper 2 to 4 decoder in
order to get the outputs, Y7 to Y4. These are the higher four minterms.
4 to 16 Decoder This can be implemented using using 3 to 8 decoders. We know that 3 to 8 de-
coder has three inputs A2, A1 & A0 and eight outputs, Y7 to Y0. Whereas, 4 to 16 decoder has four
inputs A3, A2, A1 & A0 and sixteen outputs, Y15 to Y0. We know the following formula for ﬁnding
the number of lower order decoders required.
Required number of lower order decoders=m2/m1
Substituting, m1=8 and m2=16 in the above formula,
Required number of 3 to 8 decoders=16/8=2
Therefore, we require two 3 to 8 decoders for implementing one 4 to 16 decoder. The block diagram
of 4 to 16 decoder using 3 to 8 decoders as shown in the following Figure 6.8.
Figure 6.8: Block diagram of 4 to 16 decoder
The parallel inputs A2, A1 & A0 are applied to each 3 to 8 decoder. The complement of input,
A3 is connected to Enable, E of lower 3 to 8 decoder in order to get the outputs, Y7 to Y0. These are
the lower eight minterms. The input, A3 is directly connected to Enable, E of upper 3 to 8 decoder
in order to get the outputs, Y15 to Y8. These are the higher eight minterms.
6.1.4 BCD to seven segment Decoder
In most practical applications, seven segment displays are used to give a visual indication of the
output states of digital ICs such as decade counters, latches etc. These outputs are usually in four
bit BCD (Binary coded decimal) form, and thus not suitable for directly driving seven segment
displays. The special BCD to seven segment decoder/driver ICs are used to convert the BCD signal
into a form suitable for driving these displays. The tabulation of the seven segments activated
during each digit display is shown in the Figure 6.9.

6.1. DECODER 55
Figure 6.9: Seven segment display table
The truth table depends on the construction of 7-segment display. If 7-segment display is com-
mon anode, the segment driver output must be active low to glow the segment. In case of common
cathode type 7-segment display, the segment driver output must be active high to glow the seg-
ment. The above table in the Figure 6.9 shows the BCD to 7 segment decoder/driver with common
cathode display.
K-map simpliﬁcation of BCD to seven segment display
Figure 6.10: K-map for BCD to 7 segment display
Figure 6.11: Logic diagram for BCD to 7 segment display

6.2 Binary Encoder:
A binary encoder has 2n
input lines and n output lines, hence it encodes the information from
2n
inputs into an n-bit code. From all the input lines, only one of an input line is activated at a
time and depending on the input line, it produces the n bit output code. The Figure 6.12 shows
the block diagram of binary encoder which consists of 2n
input lines and n output lines. It trans-
lates decimal number to binary number. The output lines of an encoder correspond to either true
binary equivalent or in BCD coded form of the binary for the input value. Some of these binary
encoders include decimal to binary encoders, decimal to octal, octal to binary encoders, decimal
to BCD encoders etc. Depending on the number of input lines, digital or binary encoders produce
the output codes in the form of 2 or 3 or 4 bit code.
Figure 6.12: Binary encoder
6.2.1 Parity Encoder IC(74XX148)
The IC 74XX148 is an 8-input priority encoder. It accepts data from eight active low inputs and
provides a binary representation on the three active-low outputs. A priority is assigned to each in-
put so that when two or more inputs are simultaneously active, the input with the highest priority
is represented on the output. Input I0 has least priority and input I7 has highest priority. Figure
6.13 shows the pin diagram and logic symbol for IC74XX148.
Figure 6.13: IC74XX148
¯EI is the active low enable input. A high on ¯EI will force all outputs to the inactive (high) state and
allow new data to settle without producing erroneous information at the outputs. A group signal
( ¯GS)is asserted when the device is enable and one or more of the inputs to the encoder are active.
Enable output ( ¯EO) is an active low signal that can be used to cascade several priority encoder
device to form a larger priority encoding system. When all inputs are high i.e none of the input is
active. ¯EO goes low indicating that no priority event connected to the IC is present. In cascaded

6.3. THREE STATE DEVICES: 57
priority encoders, ¯EO is connected to the ¯EI input of the next lower priority encoder. The table
6.14 shows truth table for 74XXX148 priority encoder.
Figure 6.14: Truth table of IC74XX148
6.3 Three state devices:
These are the devices whose output may be 0, 1 or high impedance. The key parameter of three
state device is ENABLE PIN that puts the device in low impedance or high impedance mode.
6.3.1 Three-State Buffers:
The most basic three-state device is a three-state buffer, often called a three-state driver. The logic
symbols for four physically different three-state buffers are as shownn in the Figure 6.15.
Figure 6.15: 3-state device symbol
The Figure 6.15 shows (a)Non-inverting, active-high enable (b)Non-inverting, active-low enable
(c) Inverting, active-high enable (d)Inverting, active-low enable 3-state buffers. The basic symbol
is that of a non-inverting buffer (a,b) or an inverter (c,d). The extra signal at the top of the symbol
is a three-state enable input, which may be active high (a,c) or active low (b,d). When the enable
input is asserted, the device behaves like an ordinary buffer or inverter. When the enable input is
negated, the device output ﬂoats; that is, it goes to high impedance (Hi-Z), disconnected state and
functionally behaves as if it weren’t even there.

Figure 6.16: Eight Sources sharing a three-state parity line
The Figure 6.16 shows an example of how the three-state devices allow multiple sources to share a
single party line, as long as only one device talks on the line at a time. Three input bits, SSRC2–SSRC0,
select one of eight sources of data that may drive a single line, SDATA. A 3-to-8 decoder, the 74x138,
ensures that only. One of the eight SEL lines is asserted at a time, enabling only one three-state
buffer to drive SDATA. However, if not all of the EN lines are asserted, and then none of the three-
state buffers is enabled, the logic value on SDATA will be undefined.
Typical three-state devices are designed so that they go into the Hi-Z state faster than they
come out of the Hi-Z state (in terms of the specifications in a data book, tpLZ and tpHZ are both
less than tpZL and tpZH) i.e. if the outputs of two three-state devices are connected to the same
party line, and we simultaneously disable one and enable the other, the first device will get off
the party line before the second one gets on. This is important because, if both devices were to
drive the party line at the same time, and if both were trying to maintain opposite output values
(0 and 1), then excessive current would flow and create noise in the system, often called fight-
ing. Unfortunately, delays and timing skews in control circuits make it difficult to ensure that the
enable inputs of different three-state devices change simultaneously. Even when this is possible,
a problem arises if three-state devices from different - speed logic families (or even different ICs
manufactured on different days) are connected to the same party line. The turn-on time (tpZL or
tpZH) of a fast device may be shorter than the turn-off time (tpLZ or tpHZ) of a slow one, and the
outputs may still fight. The only really safe way to use three-state devices is to design control logic
that guarantees a dead time on the party line during which no one is driving it.

6.3. THREE STATE DEVICES: 59
Figure 6.17: Timing diagram for the three-state parity line
The dead time must be long enough to account for the worst-case differences between turn-off
and turn-on times of the devices and for skews in the three-state control signals. Figure 6.17 shows
the operation for the party line of Figure 6.16 i.e. a drawing convention for three-state signals when
in the Hi-Z state, they are shown at an undeﬁned level halfway between 0 and 1.
6.3.2 Standard SSI and MSI Three-State Buffers
Like logic gates, several independent three-state buffers may be packaged in a single SSI IC. Figure
6.18 shows the pin-outs of 74x125 and 74x126, each of which contains four independent non-
inverting three-state buffers in a 14-pin package. The three-state enable inputs in the 74x125 are
active low, and in the 74x126, they are active high.
Figure 6.18: Pinouts of the 74x125 and 74x126 three-state buffers
Most party-line applications use a bus with more than one bit of data. For example, in an 8-bit
microprocessor system, the data bus is eight bits wide, and peripheral devices normally place data
on the bus eight bits at a time. Thus, a peripheral device enables eight three-state drivers to drive
the bus, all at the same time. Independent enable inputs, as in the 74x125 and 74x126, are not
necessary. Thus, to reduce the package size in wide-bus applications, most commonly used MSI
parts contain multiple three-state buffers with common enable inputs.
Figure 6.19 shows the logic diagram and symbol for a 74x541 octal non-inverting three-state buffer.
Octal means that the part contains eight individual buffers. Both enable inputs, G1_L and G2_L,
must be asserted to enable the device’s three-state outputs. The little rectangular symbols inside
the buffer symbols indicate hysteresis, an electrical characteristic of the inputs that improves noise
immunity. The 74x541 inputs typically have 0.4 volts of hysteresis.
Figure 6.19: 74x541 octal three-state buffer

A bus transceiver is typically used between two bidirectional buses, as shown in the Figure 6.20.
Three different modes of operation are possible, depending on the state of G_L and DIR, as shown
in the Table 6.21. As usual, it is the designer’s responsibility to ensure that neither bus is ever driven
simultaneously by two devices. However, independent transfers where both buses are driven at the
same time may occur when the transceiver is disabled, as indicated in the last row of the table.
Figure 6.20: Bidirectional buses and transceiver operation
Figure 6.21: Modes of operation of bus transceiver
6.4 Digital multiplexer
In digital systems, many times it is necessary to select single data line from several data-input
lines and the data from the selected data line should be available on the output. The digital circuit
which does this task is a multiplexer. It is a digital switch. It allows digital information from several
sources to be routed onto a single output line as shown in the Figure 6.22. The basic multiplexer
has several data-input lines and a single output line. The selection of a particular input line is
controlled by a set of selection lines. Since multiplexer selects one of the input and routes it to
output, it is also known as data selector. Normally, there are 2n
input lines and n selection lines
whose bit combination determine which input is selected. Therefore, multiplexer is many to one
and it provides the digital equivalent of an analog selector switch.

6.4. DIGITAL MULTIPLEXER 61
Figure 6.22: Multiplexer
6.4.1 The 74xx151 8 to 1 Multiplexer
The 74XX151 is a 8 to 1 multiplexer. It has eight inputs. It provides two outputs, one is active low.
The Figure 6.23 shows the logic symbol for 74XX151. As shown in the logic symbol, there are three
select inputs C,B and A which select one of the eight inputs. The 74XX151 is provided with active
enable input.
Figure 6.23: Logic symbol of IC74XX151
The table 6.24 shows the truth table for 74XX151. In this truth table for each input combination,
output is not speciﬁed in 1s and 0s. Because we know that, multiplexer is a data switch, it does not
generate any data of its own, but it simple passes external input data from the selected input to the
output. Therefore, the two output columns represent data Dn and ¯Dn respectively.

Figure 6.25: Logic diagram of IC74XX151
6.4.2 The 74xx157 Quad 2-input Multiplexer
The IC 74xx157 is a quad 2-input multiplexer which selects four bits of data from two sources under
the control of common select input(S). The enable input ¯E is active low, when ¯E is high, all of the
outputs(Y) are forced low regardless of all other input conditions. Moving data from two groups
register to four common output buses is a common use of IC 74XX157. The state of the select input
determines the particular register from which the data comes. The following Figure 6.26 and 6.27
shows logic symbol and truth table for IC74XX157 respectively.
Figure 6.26: Logic symbol of IC74XX157

6.5. DEMULTIPLEXER 63
6.4.3 Expanding multiplexers
Several digital multiplexer ICs are available such as 74X150(16 to 1), 74X151(8 to 1), 74X157(Dual 2
input) and 74X153(Dual 4 to 1) multiplexer. It is possible to expand the range of inputs for multi-
plexer beyond the available range in the integrated circuit. This can be accomplished by intercon-
necting several multiplexers. For example two 74XX151(8 to 1) multiplexer can be used together
to form a 16 to 1 multiplexers, two 74XX150 (16 to 1 multiplexers) can be used together to from a
32 to 1 multiplexer and so on.
6.5 Demultiplexer
A Demultiplexer is a data distributor read as DEMUX. It is quite opposite to multiplexer or MUX.
It is a process of taking information from one input and transmitting over one of many outputs.
Figure 6.28: Demultiplexer
DEMUX are used to implement general-purpose logic systems. A demultiplexer takes one single
input data line and distributes it to any one of a number of individual output lines one at a time.
Demultiplexing is the process of converting a signal containing multiple analog or digital signals
backs into the original and separate signals. A demultiplexer of 2n
outputs has n select lines.
6.5.1 1 to 8 Demultiplexer:
A 1 line to 8 line demultiplexer has one input, three select input lines and eight output lines. It
distributes the one input data into 8 output lines depending on the selected input. Din is the input
data, S0, S1 and S2 are select inputs and Y0, Y1, Y2, Y3, Y4, Y5, Y6 and Y7 are the outputs.
Figure 6.29: Block diagram of 1 to 8 demultiplexer

Figure 6.30: Circuit diagram of 1 to 8 demultiplexer
6.6 Exclusive-OR Gates and Parity Checkers
An Exclusive OR (XOR) gate is a 2-input gate whose output is 1 if exactly one of its inputs is 1.
Stated another way, an XOR gate produces a 1 output if its inputs are different. An Exclusive NOR
(XNOR) or equivalence gate is just the opposite, it produces a 1 output if its inputs are the same.
The corresponding truth table for these functions is shown in the table 6.32.
Figure 6.31: Truth table for XOR and XNOR gates
The XOR operation is sometimes denoted by the symbol ⊕, that is
X ⊕Y = ¯X .Y + ¯Y .X
Although EXCLUSIVE OR is not one of the basic functions of switching algebra, discrete XOR gates
are fairly commonly used in practice. Most switching technologies cannot perform the XOR func-
tion directly. Instead, they use multi-gate designs like the ones shown in the Figure ??.
Figure 6.32: Multi-gate design for XOR function

6.6. EXCLUSIVE-OR GATES AND PARITY CHECKERS 65
Figure 6.33: Equivalent Symbol for (a)XOR gate (b)XNOR gate
The logic symbols for XOR and XNOR functions are shown in the Figure 6.33. There are four equiv-
alent symbols for each function. All of these alternatives are a consequence of a simple rule:
• Any two signals (inputs or output) of an XOR or XNOR gate may be complemented without
changing the resulting logic function.
• In bubble-to-bubble logic design, we choose the symbol that is most expressive of the logic
function being performed.
Four XOR gates are provided in a single 14-pin SSI IC, the 74x86 shown in the Figure 6.34. New
SSI logic families do not offer XNOR gates, although they are readily available in FPGA and ASIC
libraries and as primitives in HDLs.
Figure 6.34: Pin outs of the 74x86 quadruple 2-input XOR gate parity circuits
As shown in the Figure 6.35, n XOR gates may be cascaded to form a circuit with (n +1) inputs and
a single output. This is called an odd-parity circuit, because its output is 1 if an odd number of its
inputs are 1. The circuit in 6.35(b) is also an odd parity circuit, but it is faster because its gates are
arranged in a tree-like structure. If the output of either circuit is inverted, we get an even-parity
circuit, whose output is 1 if even numbers of its inputs are 1.

Figure 6.35: Cascading XOR gates (a)Daisy-Chain Connection (b)Tree Structure
6.6.1 74x280 (9-Bit) Parity Generator
Rather than building a multi-bit parity circuit with discrete XOR gates, it is more economical to put
all of the XORs in a single MSI package with just the primary inputs and outputs available at the
external pins. The 74x280 9-bit parity generator, shown in the Figure 6.36 is such a device. It has
nine inputs and two outputs that indicate whether an even or odd number of inputs are 1.
Figure 6.36: 74x280 9-bit odd/even parity generator (a)Logic Diagram including pin numbers for a
standard 16-pin dual-in-line package (b)Traditional logic symbol
6.6.2 Parity-Checking Applications
Error-detecting codes that use an extra bit, called a parity bit, are used to detect errors in the trans-
mission and storage of data. In an even parity code, the parity bit is chosen so that the total number
of 1 bits in a code word is even. Parity circuits like the 74x280 are used both to generate the correct
value of the parity bit when a code word is stored or transmitted and to check the parity bit when
a code word is retrieved or received.

6.6. EXCLUSIVE-OR GATES AND PARITY CHECKERS 67
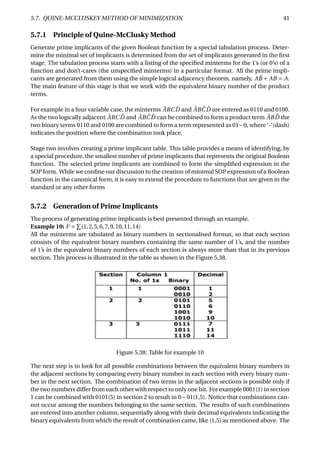
Figure 6.37: Parity generation and checking for an 8-bit-wide memory system
The Figure 6.37 shows how a parity circuit might be used to detect errors in the memory of a mi-
croprocessor system. The memory stores 8-bit bytes, plus a parity bit for each byte. The micropro-
cessor uses a bidirectional bus D[0:7] to transfer data to and from the memory. Two control lines,
RD and WR, are used to indicate whether a read or write operation is desired, and an ERROR signal
is asserted to indicate parity errors during read operations.
To store a byte into the memory chips, we specify an address (not shown), place the byte on D[0–7],
generate its parity bit on PIN, and assert WR. The AND gate on the I input of the 74x280 ensures
that I is 0 except during read operations, so that during writes the 74x280’s output depends only
on the parity of the D-bus data. The 74x280’s ODD output is connected to PIN, so that the total
number of 1s stored is even.
To retrieve a byte, we specify an address (not shown) and assert RD. The byte value appears on
DOUT[0–7] and its parity appears on POUT. A 74x541 drives the byte onto the D bus, and the
74x280 checks its parity. If the parity of the 9-bit word DOUT[0–7], POUT is odd during a read, the
ERROR signal is asserted.
Parity circuits are also used with error-correcting codes such as the Hamming codes. We can cor-
rect errors in hamming code as shown in the Figure 6.38. A 7-bit word, possibly containing an
error, is presented on DU[1–7]. Three 74x280s compute the parity of the three bit-groups deﬁned
by the parity-check matrix. The outputs of the 74x280s form the syndrome, which is the number
of the erroneous input bit, if any. A 74x138 is used to decode the syndrome. If the syndrome is
zero, the NOERROR_L signal is asserted (this signal also could be named ERROR). Otherwise, the
erroneous bit is corrected by complementing it. The corrected code word appears on the DC_L
bus.
Note: The active-low outputs of the 74x138 led us to use an active-low DC_L bus. If we required
an active-high DC bus, we could have put a discrete inverter on each XOR input or output, or used
a decoder with active-high outputs, or used XNOR gates.

Figure 6.38: Error-Correcting Circuit for a 7-bit Hamming Code
6.7 Digital Logic Comparator
A magnitude digital Comparator is a combinational circuit that compares two digital or binary
numbers in order to ﬁnd out whether one binary number is equal, less than or greater than the
other binary number. We logically design a circuit for which we will have two inputs, one for A and
other for B and have three output terminals, one for A > B condition, one for A = B condition and
one for A < B condition.
Figure 6.39: Block diagram of comparator
6.7.1 IC 7485 (4-bit Comparator)
IC 7485 is a 4-bit comparator. It can be used to compare two 4-bit binary words by grounding
I(A < B), I(A > B) and connector input I(A = B) to VCC . These ICs can be cascaded to compare
words of almost any lenth. Its 4-bit inputs are weighted (A0-A3) and (B0-B3), where A3 and B3 are
the most signiﬁcant bits. The Figure 6.40 shows the logic symbol and pin diagram of IC7485. The
operation of IC7485 is described in the function table showing all possible logic conditions.

6.8. ADDERS AND SUBTRACTERS 69
Figure 6.40: Logic symbol, pin diagram and function table of IC7485
6.8 Adders and Subtracters
Digital computers perform various arithmetic operations. The most basic operation is the addition
of two binary digits. This simple addition consists of four possible elementary operations, namely,
0+0 = 0
0+1 = 1
1+0 = 1
1+1 = (10)2 The first three operation produce a sum whose length is one digit, but when the last
operation is performed, sum is two digits. The higher significant bit of this result is called a carry
and lower significant bit is called sum. The logic circuit which performs this operation is called a
half-adder. The circuit which performs addition of three bits (two significant bits and a previous
carry) is a full-adder.
6.8.1 Half Adder
Half adder operation needs two binary inputs: augend and addend bits and two binary outputs:
sum and carry. The truth table shown in Figure 6.41 gives the relation between input and output
variable for half adder operation.
Figure 6.41: Block schematic of half-adder
Figure 6.42: Truth table of half-adder

Figure 6.43: K-map for half-adder
Figure 6.44: Logic diagram of half-adder
Limitations of half adder In multi-digit addition, we have to add two bits along with the carry
of previous digit addition. Effectively, such addition requires addition of three bits. This is not
possible with half-adder. Hence half-adder are not used in practice.
6.8.2 Full Adder
Full Adder is a combinational circuit that forms the arithmetic sum of three inputs bits. It consists
of three inputs and two outputs. Two of the input variables, denoted by A and B, represent the
two signiﬁcant bits to be added. The third input Cin, represents the carry from previous lower
signiﬁcant position. The truth table for full-adder is shown in Figure 6.45.
Figure 6.45: Truth table for full adder
Figure 6.46: Block schematic of full adder

Figure 6.47: K-map simplification of full adder
The simplified expressions obtained from K-map are as follows:
Cout = AB + ACin +BCin
Sum = ¯A. ¯B.Cin + ¯A.B. ¯Cin + A. ¯B. ¯Cin + ABCin
Figure 6.48: Circuit diagram of full adder
The boolean function for sum can be further simplified as follows:
With this simplified boolean function circuit, full adder can be implemented as shown in the Fig-
ure 6.49.
Figure 6.49: Simplified full adder circuit

6.8.3 Half subtracter
Half subtracter is a combinational circuit capable of subtracting a binary number from another
binary number. It produces two outputs: difference and borrow. The borrow output speciﬁes
whether a binary number 1 is borrowed to perform subtraction or not. The Figure ?? shows the
graphic symbol of half-subtracter. The inputs are A and B. The output D is the result of subtraction
of B from A and output B0 is the borrow output.
Figure 6.50: Graphic symbol of half-subtracter
Figure 6.51: Truth Table of half-subtracter
Figure 6.52: Logic diagram of half-subtracter
6.8.4 Full Subtracter
A full subtracter is a combinational circuit that performs a subtraction between two bits, taking
into account borrow of the lower signiﬁcant stage. This circuit has three inputs and two outputs.
The three inputs are A, B and Bin, denote the minuend, subtrahend and previous borrow respec-
tively. The two outputs, D and Bout represent the difference and output borrow respectively. The
Table 6.53 shows the truth table for full-subtracter.
Figure 6.53: Truth Table of full-subtracter

Figure 6.54: K-map for Full-subtracter
Figure 6.55: Logic diagram for full-subtracter
The Boolean function for D (difference) can be further simpliﬁed as follows:
Figure 6.56: Implementation of full subtacter
A full subtracter can also be implemented with two half subtracters and one OR gate, as shown in
the Figure 6.57. The difference output from the second half subtracter is the exclusive-OR of Bin
and the output of the ﬁrst half subtracter, which is same as difference output of full subtracter.
Figure 6.57: Implementation of a full subtracter with two half subtacters and an OR gate
The borrow output for the circuit shown in above Figure 6.57 can be given as follows:

This boolean function is same as borrow out of the full-subtracter. Therefore, we can implement
full-subtracter using two half-subtracters and an OR gate.
6.8.5 Ripple carry adder
Multiple full adder circuits can be cascaded in parallel to add an N-bit number. For an N- bit
parallel adder, there must be N number of full adder circuits. A ripple carry adder is a logic circuit
in which the carry-out of each full adder is the carry in of the succeeding next most signiﬁcant
full adder. It is called a ripple carry adder because each carry bit gets rippled into the next stage.
In a ripple carry adder the sum and carry out bits of any half adder stage is not valid until the
carry in of that stage occurs. Propagation delays inside the logic circuitry is the reason behind
this. Propagation delay is time elapsed between the application of an input and occurrence of the
corresponding output. Consider a NOT gate, when the input is "0" the output will be "1" and vice
versa. The time taken for the NOT gate’s output to become "0" after the application of logic "1"
to the NOT gate’s input is the propagation delay here. Similarly the carry propagation delay is the
time elapsed between the application of the carry in signal and the occurrence of the carry out
(Cout) signal. Circuit diagram of a 4-bit ripple carry adder is shown in the Figure 6.58.
Figure 6.58: 4 bit ripple adder
Sum out S0 and carry out Cout of the Full Adder 1 is valid only after the propagation delay of Full
Adder 1. In the same way, Sum out S3 of the Full Adder 4 is valid only after the joint propagation
delays of Full Adder 1 to Full Adder 4. In simple words, the ﬁnal result of the ripple carry adder is
valid only after the joint propogation delays of all full adder circuits inside it. To reduce the com-
putation time, there are faster ways to add two binary numbers by using carry lookahead adders.
They work by creating two signals P and G known to be Carry Propagator and Carry Generator.
The carry propagator is propagated to the next level whereas the carry generator is used to gener-
ate the output carry, regardless of input carry. The block diagram of a 4-bit Carry Lookahead Adder
is shown in the Figure 6.59.
Figure 6.59: Carry lookahead adder
The number of gate levels for the carry propagation can be found from the circuit of full adder.
The signal from input carry Cin to output carry Cout requires an AND gate and an OR gate, which
constitutes two gate levels. So if there are four full adders in the parallel adder, the output carry C5
would have 2 X4=8 gate levels from C1 to C5. For an n-bit parallel adder, there are 2n gate levels to
propagate.

Design Issues The corresponding boolean expressions are given here to construct a carry looka-
head adder. In the carry-lookahead circuit, we need to generate the two signals carry propaga-
tor(P) and carry generator(G).
Pi = Ai ⊕Bi
Gi = Ai .Bi
The output sum and carry can be expressed as
Sumi = Pi ⊕Ci
Ci+1 = Gi +(Pi .Ci )
Having these we could design the circuit. We can now write the Boolean function for the carry
output of each stage and substitute for each Ci its value from the previous equations:
C1 = G0 +P0.C0
C2 = G1 +P1.C1 = G1+P1.G0+P1.P0.C0
C3 = G2 +P2.C2 = G2P2.G1 +P2.P1.G0 +P2.P1.P0.C0
C4 = G3 +P3.C3 = G3.P3.G2.P3.P2.G1 +P3.P2.P1.G0 +P3.P2.P1.P0.C0
6.8.6 MSI ADDERS
The 74x283 is a 4-bit binary adder that forms its sum and carry outputs with just a few levels of
logic, using the carry look-ahead technique. The older 74x83 is identical except for its pin-out,
which has non standard locations for power and ground. The logic diagram for the 74x283 has
just a few differences from the general carry look-ahead design that we described in the preceding
subsection. First of all, its addends are named A and B instead of X and Y; no big deal. Second,
it produces active-low versions of the carry-generate (gi ) and carry propagate (pi ) signals, since
inverting gates are generally faster than non-inverting ones. Third, it takes advantage of the fact
that we can algebraically manipulate the half-sum equation as follows:
An AND gate with an inverted input can be used instead of an XOR gate to create each half-sum
bit. Finally, the 74x283 creates the carry signals using an INVERT-OR-AND structure (the DeMor-
gan equivalent of an AND-OR-INVERT), which has about the same delay as a single CMOS or TTL
inverting gate. This requires some explanation, since the carry equations that we derived in the
preceding subsection are used in a slightly modiﬁed form.
In particular, the ci equation uses the term pi .gi instead of gi . This has no effect on the output,
since pi is always 1 when gi is 1. However, it allows the equation to be further simpliﬁed and this
leads to the following carry equations, which are used by the circuit

The propagation delay from the C0 input to the C4 output of the 74x283 is very short, about the
same as two inverting gates. As a result, fairly fast group ripple adders with more than four bits can
be made simply by cascading the carry outputs and inputs of 74x283s, as shown in Figure 6.60 for
a 16-bit adder. The total propagation delay from C0 to C16 in this circuit is about the same as that
of eight inverting gates.
Figure 6.60: Circuit diagram of 74x283
Figure 6.61: Pin diagram of 74x283
6.9 MSI Arithmetic and Logic Units
An arithmetic and logic unit (ALU) is a combinational circuit that can perform any of a number of
different arithmetic and logical operations on a pair of b-bit operands. The operation to be per-

6.9. MSI ARITHMETIC AND LOGIC UNITS 77
formed is specified by a set of function-select inputs. Typical MSI ALUs have 4-bit operands and
three to five function select inputs, allowing up to 32 different functions to be performed. Figure
6.62 is a logic symbol for the 74x181 4-bit ALU. The operation performed by the 74x181 is selected
by the M and S3–S0 inputs. Note that the identifiers A, B and F in the table refer to the 4-bit words
A3–A0, B3–B0, and F3–F0. The 74x181’s M input selects between arithmetic and logical opera-
tions. When M =1, logical operations are selected, and each output Fi is a function only of the
corresponding data inputs, Ai and Bi. No carries propagate between stages, and the CIN input is
ignored. The S3–S0 inputs select a particular logical operation. Any of the 16 different combina-
tional logic functions on two variables may be selected. When M = 0, arithmetic operations are
selected, carries propagate between the stages, and CIN is used as a carry input to the least sig-
nificant stage. For operations larger than four bits, multiple 74x181 ALUs may be cascaded like
the group-ripple adder with the carry-out (COUT) of each ALU connected to the carry-in (CIN) of
the next most significant stage. The same function-select signals (M,S3–S0) are applied to all the
74x181s in the cascade.
Figure 6.62: Pin diagram of 74x181
To perform two’s-complement addition, we use S3–S0 to select the operation "A plus B plus CIN".
The CIN input of the least significant ALU is normally set to 0 during addition operations. To per-
form two’s-complement subtraction, we use S3–S0 to select the operation "A minus B minus CIN".
In this case, the CIN input of the least significant ALU is normally set to 1, since CIN acts as the
complement of the borrow during subtraction. The 74x181 provides other arithmetic operations,
such as "A minus 1 plus CIN" that are useful in some applications (e.g. decrement by 1). It also
provides a bunch of weird arithmetic operations, such as "A.B.. plus (A..B)plus CIN" that are al-
most never used in practice, but that fall out of the circuit for free. Notice that the operand inputs
A3_L–A0_L and B3_L–B0_L and the function outputs F3_L–F0_L of the 74x181 are active low.
The 74x181 can also be used with active-high operand inputs and function outputs. In this case, a
different version of the function table must be constructed. When M..1, logical operations are still
performed, but for a given input combination on S3–S0, the function obtained is precisely the dual
of the one listed in Table 6.63. When M..0, arithmetic operations are performed, but the function
table is once again different.

Figure 6.63: MSI ALU function table
6.10 Combinational Multipliers
Multiplier has an algorithm that uses n shifts and adds to multiply n-bit binary numbers. Although
the shift-and-add algorithm emulates the way that we do paper-and-pencil multiplication of deci-
mal numbers, there is nothing inherently sequential or time dependent about multiplication. That
is, given two n-bit input words X and Y, it is possible to write a truth table that expresses the 2n-bit
product P..x..Y as a combinational function of X and Y. A combinational multiplier is a logic cir-
cuit with such a truth table. Most approaches to combinational multiplication are based on the
paper-and-pencil shift-and-add algorithm.
Figure 6.64: 8X8 multiplier partial products
Figure 6.64 illustrates the basic idea for an 8x8 multiplier for two unsigned integers, multiplicand
X = x7x6x5x4x3x2x1x0 and multiplier Y = y7y6y5y4y3y2y1y0. We call each row a product compo-
nent, a shifted multiplicand that is multiplied by 0 or 1 depending on the corresponding multiplier
bit. Each small box represents one product-component bit yi xj , the logical AND of multiplier bit
yi and multiplicand bit xj . The product P = p15p14...p2p1p0 has 16 bits and is obtained by adding
together all the product components. Figure 6.64 shows one way to add up the product compo-
nents. Here, the product-component bits have been spread out to make space and each "+" box
is a full adder. The carries in each row of full adders are connected to make an 8-bit ripple adder.
Thus, the first ripple adder combines the first two product components to product the first partial
product. Subsequent adders combine each partial product with the next product component.
Sequential multipliers use a single adder and a register to accumulate the partial products. The

6.10. COMBINATIONAL MULTIPLIERS 79
partial-product register is initialized to the ﬁrst product component and for an n.n-bit multipli-
cation, n.1 steps are taken and the adder is used n.1 times, once for each of the remaining n.1
product components to be added to the partial-product register. Some sequential multipliers use
a trick called carry-save addition to speed up multiplication. The idea is to break the carry chain
of the ripple adder to shorten the delay of each addition. This is done by applying the carry output
from bit i during step j to the carry input for bit i + 1 during the next step, j + 1. After the last
product component is added, one more step is needed in which the carries are hooked up in the
usual way and allowed to ripple from the least to the most signiﬁcant bit.
Figure 6.65: 4x4 multiplier partial products
Figure 6.66: 4X4 combinational multiplier with carry save
Figure 6.67: 4X4 combinational multiplier with carry save addition

Digital Electronics

More Related Content

What's hot

Similar to Digital Electronics

Recently uploaded

Digital Electronics