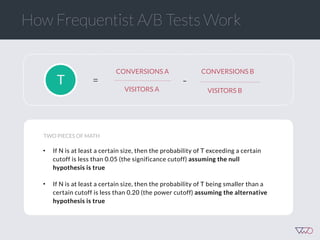
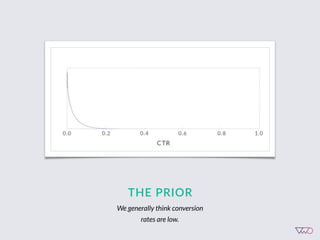
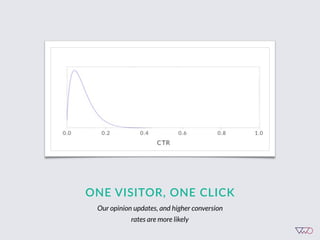
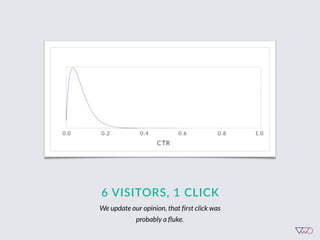
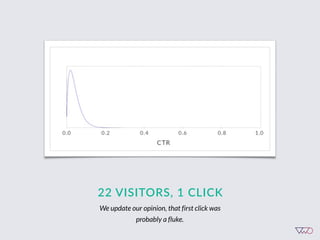
The document discusses the principles of Bayesian statistics and compares them to frequentist approaches in A/B testing, emphasizing the importance of selecting appropriate null and alternative hypotheses. It highlights the misinterpretations of significance and emphasizes the role of prior opinions and gathering evidence in Bayesian analysis to form more reliable conclusions. Additionally, it suggests practical steps for implementing Bayesian A/B tests and outlines the advantages of this approach over traditional methods.

1. BAYESIAN STATISTICS
Chris Stucchio
@stucchio
https://chrisstucchio.com
| https://github.com/stucchio
09 Oct 2015

2. INGREDIENTS:
A Null Hypothesis
Version A and B have the same conversion rate
An Alternative Hypothesis
Version B’s conversion rate is 5% or more higher than A’s
A Test Statistic
Which we expect to be close to 0 if the null hypothesis is true and far from 0 if it is false. For example
T =
CONVERSIONS A
VISITORS A
CONVERSIONS B
VISITORS B
-
How Frequentist A/B Tests Work

3. • If N is at least a certain size, then the probability of T exceeding a certain
cutoff is less than 0.05 (the significance cutoff) assuming the null
hypothesis is true
• If N is at least a certain size, then the probability of T being smaller than a
certain cutoff is less than 0.20 (the power cutoff) assuming the alternative
hypothesis is true
TWO PIECES OF MATH
T =
CONVERSIONS A
VISITORS A
CONVERSIONS B
VISITORS B
-
How Frequentist A/B Tests Work

4. Suppose the control conversion rate is 5%, and we are seeking
a 20% lift in an experiment.
EXAMPLE
• If we have at least 7,600 samples per variation, then
there is a 5% chance of a false positive assuming
both variations are equal.
• There is also a 20% chance of a false negative
assuming B has at least a 6% conversion rate.
How Frequentist A/B Tests Work

5. P -VALUE
A probability of a false positive “at least as extreme” as the result
you just saw in a hypothetical A/A test.
SIGNIFICANCE LEVEL (= 100% - P-VALUE)
A probability of NOT seeing a false positive at least as extreme.
These numbers are highly dependent on your null and
alternative hypothesis, so you have to choose them carefully.
How Frequentist A/B Tests Work
(Many vendors, including VWO until recently, incorrectly referred to the significance level as “Chance to Beat Control”.)

6. You've run an A/B test. Your A/B testing software has given
you a p-value of p=0.03 for a one-tailed test.
(Note that several or none of the statements may be correct.)
• You have disproved the null hypothesis (that is, there is no difference between the variations).
• The probability of the null hypothesis being true is 0.03.
• You have proved your experimental hypothesis (that the variation is better than the control).
• The probability of the variation being better than control is 97%.
• You know, if you decide to reject the null hypothesis, the probability that you are making the
wrong decision is 3%.
• You have a reliable experimental finding in the sense that if the experiment were repeated a
great number of times, you would obtain a significant result on 97% of occasions.
WHICH OF THE FOLLOWING IS TRUE?
How Frequentist A/B Tests Work

7. ALL ARE FALSE
BUT TRY TELLING THAT TO CUSTOMERS
Study shows 100% of psychology graduates and 80% of
professors get that question wrong.
Misinterpretations of Significance: A Problem
Students Share with Their Teachers?
How Frequentist A/B Tests Work

8. A PRACTICAL QUIZ
An A/B test is run, and it is observed that B has a higher mean
than A with a p-value of 4%. What is the probability that B is
really better than A?
‣ 96%
‣ 95%
‣ 80%
How Frequentist A/B Tests Work

9. So how do we compute this probability?
A PRACTICAL QUIZ
An A/B test is run, and it is observed that B has a higher mean
than A with a p-value of 4%. What is the probability that B is
really better than A?
How Frequentist A/B Tests Work
‣ 96%
‣ 95%
‣ 80%
‣ Cannot be determined from the
information given

10. OUR FIRST BAYESIAN
CALCULATION

11. Make unrealistic assumptions to simplify the math.
(This is a pedagogical exercise.)
ASSUME THERE ARE ONLY TWO POSSIBILITIES IN THE WORLD
• Null Hypothesis (Control and Variation are Equal)
• Alternate Hypothesis (Variation beats control by at least 20%)
WE WILL ASSUME EACH OF THESE OCCURS WITH FIXED PROBABILITY
How Frequentist A/B Tests Work

12. CONSIDER A SPHERICAL COW
(Physics phrase describing calculations that illustrate the
point, but are ridiculously oversimplified.)
Our First Bayesian Calculation

13. Need to know base rate - fraction of A/B tests which actually
have true result.
Suppose base rate is 5% - i.e., 95% of ideas suck.
This means exactly 5% of tests have a variation which is
20% better than control, and 95% of tests have a
variation identical to control.
Our First Bayesian Calculation

14. TEST SAYS WIN TEST SAYS LOSE
REAL WINNER 40 (80% of 50) 10 50
REAL LOSER 47 (5% of 950) 903 950
87 913
Suppose base rate is 5% - i.e., 95% of ideas suck.
Consider 1000 A/B tests:
Our First Bayesian Calculation

15. PROBABILITY OF REAL WINNER: 40 / 87 = 46%
TEST SAYS WIN TEST SAYS LOSE
REAL WINNER 40 10 50
REAL LOSER 47 903 950
87 913
Suppose base rate is 5% - i.e., 95% of ideas suck.
Consider 1000 A/B tests:
Our First Bayesian Calculation

16. PROBABILITY OF REAL WINNER: 240 / 275 = 87%
TEST SAYS WIN TEST SAYS LOSE
REAL WINNER 240 60 300
REAL LOSER 35 665 700
275 725
Suppose base rate is 30% - i.e., 70% of ideas suck.
Consider 1000 A/B tests:
Our First Bayesian Calculation

17. Our First Bayesian Calculation
THE PRIOR
Our opinion before we
have any data

18. - PAUL SAMUELSON
When events change,I change my mind.
What do you do?

19. Our First Bayesian Calculation
THE POSTERIOR
We’ve changed our opinion
after seeing the data

20. BAYESIAN STATISTICS
‣ Come up with a
subjective Prior opinion
‣ Gather evidence
‣ Change your opinion
and form a Posterior
BAYES RULE
The mathematically
optimal way to
change your opinion

21. IMPROVING THE ACCURACY OF OUR MODEL

22. Unrealistic Assumptions
• Only possible conversion rates are 5% and 6% - why not
4.3% or 5.5%?
• Ignores cost/benefit. If B has a 3% conversion rate,
choosing it is very bad. If B has a 4.99% conversion rate,
choosing it is almost harmless.
• Results in previous test based on looking at results only
once, then making decision. Our users check test
results every day.

23. THERE ARE MORE THAN TWO POSSIBLE CONVERSION RATES
It’s not realistic to assume that conversion rates are either 5% or 6%.
This is just not a useful picture of reality:

24. THERE ARE MORE THAN TWO POSSIBLE CONVERSION RATES
Conversion rate can be 4%, 5%, 5.34%, 6.21%, or any other value
between 0 and 100%. Represent with continuous functions

25. CREDIBLE INTERVALS
99% probability that true conversion rate is at least
16.9% and not more than 23.3%.

26. THE PRIOR
We generally think conversion
rates are low.

27. ONE VISITOR, ONE CLICK
Our opinion updates, and higher conversion
rates are more likely

28. 6 VISITORS, 1 CLICK
We update our opinion, that first click was
probably a fluke.

29. 22 VISITORS, 1 CLICK
We update our opinion, that first click was
probably a fluke.

30. 207 VISITORS, 4 CLICKS
We are confident the CR is
approximately 2%.

31. PRIORS ARE SUBJECTIVE
Bayesian Analysis starts by “pulling a prior out
of your posterior”.

32. POSTERIORS CONVERGE
Theorem (stylized): Rational Bayesians never “agree
to disagree” when sufficient data is available.

33. JOINT POSTERIORS - REPRESENTING ALL VARIATIONS
So far we only form opinions about conversion
rate of one variation.
Need to represent probability of things like “conversion
rate of A is 4.5% and conversion rate of B is 6.3%”.
SOLUTION IS CALLED
JOINT POSTERIOR

34. TWO POSTERIORS ON TWO DIFFERENT
CONVERSION RATES

35. COMBINE TO FORM JOINT POSTERIOR
Point (0.10, 0.15) represents “A has a conversion rate of
10%, B has a conversion rate of 15%”.

36. Opinions About the World
• Start with an uneducated opinion, the prior.
• Gather data.
• Change your opinion and end up educated
with a posterior.

37. MAKING DECISIONS
Maximize Revenue, don’t Test for Truth

38. • Designed by and for scientists.
• Question: “Do jellybeans cause acne?”
• Run A/B test, give B group jellybeans. Measure amount of acne in
both groups.
• If p < 0.05, publish paper in good journal - “Jellybeans cause acne.”
• If p >= 0.05, publish paper in bad journal - “Jellybeans don’t cause
acne, but we did a good experiment to check.”
Hypothesis Testing
Goal of hypothesis testing is to avoid
publishing false results.

39. Think Like a Trader
look for interesting phenomena, and publish papers when they find them.
• CRO is more like trading - the goal is to get more conversions = $.
• If A == B, thinking A > B is harmless; instead of getting a 5% conversion rate
with B, you are stuck with a 5% conversion rate with A. Money lost: $0.
• If the CR of A is 4.9% and B is 5%, a wrong decision costs only 0.1%. If CR of
A is 4%, a wrong decision costs 10x more!
buy and sell stocks with the goal of making money.
A SCIENTISTS
A TRADER

40. B > A (50% CHANCE) B = A (50% CHANCE)
DEPLOY A Lose Even
DEPLOY B Win Even
ASYMMETRIC COSTS AND FALSE POSITIVES
Smart decision: Deploy B.
Heads you win, tails you don’t lose.

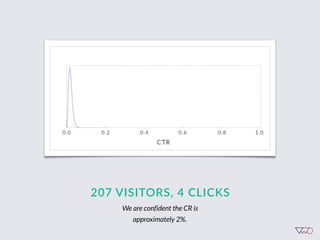
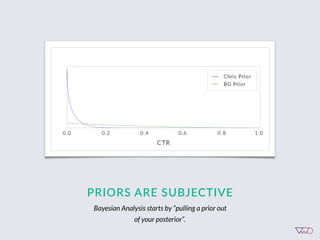
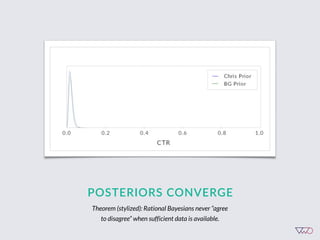
41. Cost of a Mistake
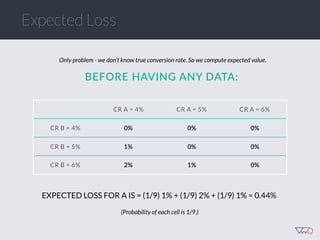
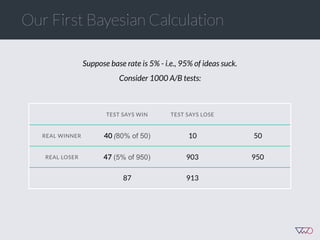
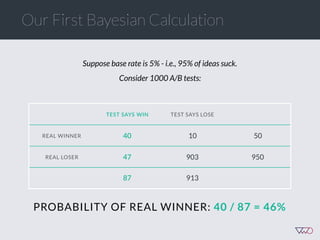
Suppose we choose variation x. The cost of this choice is:
Loss[x] = Max (CR[i] - CR[x])
This is simple opportunity cost - it’s the difference
between the best choice and our choice.
Key point: bigger mistakes cost us more money.

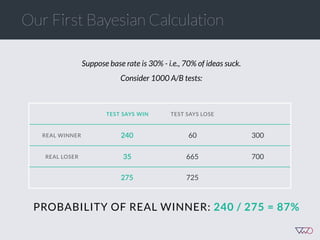
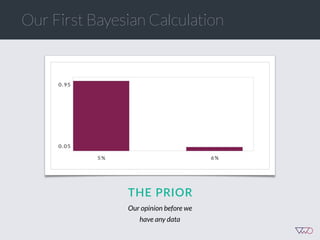
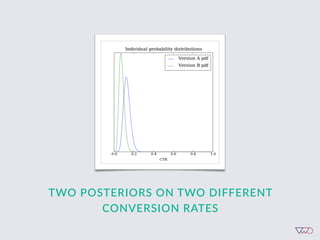
42. Cost of a Mistake
EXAMPLE
A. 5%
‣ Loss[A] = Max(5% - 5%, 6% - 5%, 4.5% - 5%) = 1%
‣ Loss[B] = Max(5% - 6%, 6% - 6%, 4.5% - 6%) = 0%
‣ Loss[C] = Max(5% - 4.5%, 6% - 4.5%, 4.5% - 4.5%) = 1.5%
B. 6% C. 4.5%

43. Expected Loss
CR A = 4% CR A = 5% CR A = 6%
CR B = 4% 0% 0% 0%
CR B = 5% 1% 0% 0%
CR B = 6% 2% 1% 0%
BEFORE HAVING ANY DATA:
Only problem - we don’t know true conversion rate. So we compute expected value.
EXPECTED LOSS FOR A IS = (1/9) 1% + (1/9) 2% + (1/9) 1% = 0.44%
(Probability of each cell is 1/9.)

44. Expected Loss
CR A = 4% CR A = 5% CR A = 6%
CR B = 4% 0% 1% 2%
CR B = 5% 0% 0% 1%
CR B = 6% 0% 0% 0%
BEFORE HAVING ANY DATA:
Only problem - we don’t know true conversion rate. So we compute expected value.
EXPECTED LOSS FOR B IS = (1/9) 1% + (1/9) 2% + (1/9) 1% = 0.44%
No decision, loss > threshold of caring = 0.01

45. Expected Loss
EXPECTED LOSS FOR A IS = (1/4) 1% + (1/4) 2% + (1/4) 1% = 1%
AFTER GATHERING DATA, WE RULE
OUT SOME POSSIBILITIES:
(All black cells have probability ¼, grey cells have probability 0.
WILD OVERSIMPLIFICATION.)
CR A = 4% CR A = 5% CR A = 6%
CR B = 4% 0% 0% 0%
CR B = 5% 1% 0% 0%
CR B = 6% 2% 1% 0%

46. Expected Loss
EXPECTED LOSS FOR B IS = 0% < 0.01%
AFTER GATHERING DATA, WE
RULE OUT SOME POSSIBILITIES:
CR A = 4% CR A = 5% CR A = 6%
CR B = 4% 0% 1% 2%
CR B = 5% 0% 0% 1%
CR B = 6% 0% 0% 0%
Smart Decision

47. How to run a Bayesian A/B test
• Identify a threshold of caring - a value so small that if your conversion rate
drops by less than this, you don’t care.
• Example: I sell $10,000 of product/week on a 2% conversion rate. A 0.05%
threshold of caring corresponds to a $250/week change in revenue.
• Run A/B test.
• Periodically (not more than once a week!) compute the expected loss for
each variation. If the expected loss for some variation drops below the
threshold of caring, deploy that variation.
NOT NECESSARILY A WINNER, BUT IT WON’T LOSE.

48. Advantages
• Bayesian tests are insensitive to peeking - it’s fine to stop a test early.
• “Chance to beat control” is really the chance that a variation is better than
the control
• Get additional numbers, e.g. chance to beat all - what is the probability that
B is better than A, C and D?
• Credible intervals bound uncertainty - when a winner is deployed, you’ll be
told “variation B is between 0.01% and 25% better than A”. (Confidence
intervals do NOT provide this information.)
• Easy to understand and extend. Is there a cost of switching? Want to account
for other factors? Just include it in the loss function. (Question asked by
Denis @ booking.com, and in Bayesian framework answer was obvious.)

49. MORE ACCURATE CALCULATIONS
Central Limit Theorem with
10,000 data points

50. MORE ACCURATE CALCULATIONS
Central Limit Theorem with
100 data points

51. WHY THE WORLD DIDN’T GO BAYESIAN SOONER
Bayesian calculations are 10 million times slower than frequentist - Charles Pickering
and his computers couldn’t handle it.

55. Thank You !
For any questions, you can talk to us at
chris@wingify.com
@stucchio