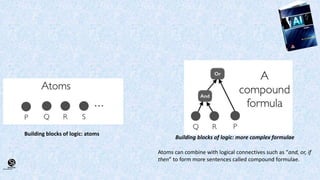
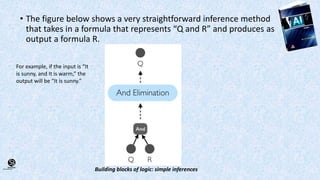
This document discusses formal logic and its applications in AI and machine learning. It begins by explaining why logic is useful in complex domains or with little data. It then describes logic-based approaches to AI that use symbolic reasoning as an alternative to machine learning. The document proceeds to explain propositional logic and first-order logic, noting how first-order logic improves on propositional logic by allowing variables. It also mentions other logics and their applications in areas like automated discovery, inductive programming, and verification of computer systems and machine learning models.

1. Formal Logic
Dr. C.V. Suresh Babu
(CentreforKnowledgeTransfer)
institute

2. (CentreforKnowledgeTransfer)
institute
Demo
https://youtu.be/IY1sPV9e9H0

3. (CentreforKnowledgeTransfer)
institute
Why?
• Logic can help AI and ML in complex domains or in domains with very
little data.
https://www.youtube.com/watch?v=K4ChzesrWKI

4. (CentreforKnowledgeTransfer)
institute
What?
• By logic we mean symbolic, knowledge-based, reasoning and other
similar approaches to AI that differ, at least on the surface, from
existing forms of classical machine learning and deep learning.
• It is crucial to keep in mind just as there are many forms of machine
learning; there are many different forms of logic-based approaches to
AI with their own sets of tradeoffs.
• Very briefly, logic-based AI systems can be thought of as high-level
programming systems that can easily encode human knowledge in a
compact and usable manner.
https://www.youtube.com/watch?v=QQwBLv9LarI

5. (CentreforKnowledgeTransfer)
institute
Introduction
• Starting with the simplest of logic systems, we have propositional
logic (sometimes called zero-order logic).
• Within propositional logic, we have objects known as sentences or
formulae that encode information.
• They denote some statement about the world.
• For building blocks, we have basic sentences known as atoms, usually
denoted by “P, Q, R, S, …..”
• For example, P might stand for “It is raining” and is an atom.
https://www.youtube.com/watch?v=_MhgsoPHvYo

6. (CentreforKnowledgeTransfer)
institute
Building blocks of logic: atoms
Building blocks of logic: more complex formulae
Atoms can combine with logical connectives such as “and, or, if
then” to form more sentences called compound formulae.

7. (CentreforKnowledgeTransfer)
institute
• Formulae give us a way to represent information.
• Then, how do we go from information we already have to new
information?
• We do this through reasoning or inference.
• Propositional logic comes equipped with a set of schemes called
inference methods.
• Inference methods can be thought of as little programs that take a set
of sentences as input and spit out one or more sentences.
https://www.youtube.com/watch?v=ywKZgjpMBUU

8. (CentreforKnowledgeTransfer)
institute
• The figure below shows a very straightforward inference method
that takes in a formula that represents “Q and R” and produces as
output a formula R.
For example, if the input is “It
is sunny, and It is warm,” the
output will be “It is sunny.”
Building blocks of logic: simple inferences

9. (CentreforKnowledgeTransfer)
institute
• All logics come equipped with a set of
inference methods like the above.
• These primitive inbuilt methods of a logic play
a role similar to that of the standard library in
any programming language.
• Given these methods, we can combine them
to form even more sophisticated methods
such as the one shown, just like you can create
large programs from a few simpler primitives.

10. (CentreforKnowledgeTransfer)
institute
Propositional logic
• Propositional logic is a good starting place for pedagogical reasons
but is unwieldy for modeling domains with a large number of objects.
• For example, let us say we want to write down the constraints that a
Sudoku puzzle should satisfy.
• Let us say we have for each number k and each row i and column j an
atom A_ijk that stands for “row i and column k contain number k”.
• With this, we can quickly write down constraints for Sudoku in
propositional logic.

11. (CentreforKnowledgeTransfer)
institute
For example, the sentence in the figure below states that the
number 5 should appear in the first row.
• We can similarly write down
other constraints for other
numbers.
• We will have a total of 9³ =
729 atoms in our constraints.
• Each atom can be true or
false, giving us a total of
possible 2⁷²⁹ states (much
much greater than the
number of physical atoms in
our universe).

12. (CentreforKnowledgeTransfer)
institute
First-order logic
• First-order logic improves upon propositional logic by introducing
atoms that can take in arguments that stand in for objects in a
domain.
For example, A(1,3,5) says that row 1 and column 3 has a 5 in it.
The figure below says that one column exists in row 1 that has
the number 5 in it.
As you can see, the representation for “Row 1 has a 5 in some
column” is much more compact in first-order logic.
• In first-order logic, instead of
having an atom A_ijk for every
combination of i, j and k, we will
have a single atom that takes in
those variables as arguments.

13. (CentreforKnowledgeTransfer)
institute
Other logics
• First-order logic forms the basis of many modern logic systems used
in research and industry.
• Many other logic systems build upon and extend first-order logic (e.g.,
second-order logic, third-order logic, higher-order logic, and modal
logic).
• Each logic adds new a dimension or feature that makes it easy to
model some aspect of the world.
• For example, logics that are known as temporal logics are used to
model time and change.

14. (CentreforKnowledgeTransfer)
institute
Applications of Logic in AI and ML
• Automated Discovery in Science
• Inductive Programming
• Automation of Mathematical Reasoning
• Verification of Computer Systems (including ML)
• Logic-like Systems along with Machine Learning Models