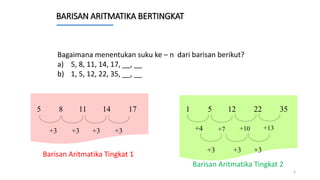
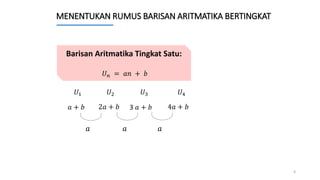
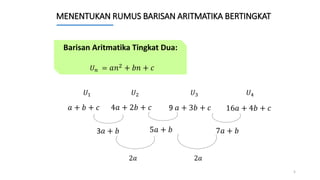
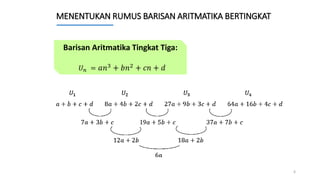
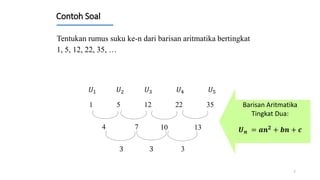
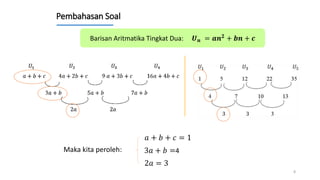
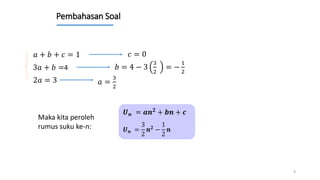
Dokumen ini membahas tentang cara menentukan suku ke-n dari berbagai jenis barisan aritmatika, termasuk barisan bertingkat 1 hingga 6. Contoh soal disertakan untuk ilustrasi dalam menemukan rumus barisan tersebut. Penjelasan mencakup penentuan notasi dan solusi untuk beberapa barisan aritmatika yang berbeda.

1. Nur Rahmi,S.Pd.M.Si.
Pembina OSN Matematika SMA
Sekolah Islam Athirah

2. TOPIK :
ALJABAR

3. BARISAN ARITMATIKA BERTINGKAT
3
Bagaimana menentukan suku ke – n dari barisan berikut?
a) 5, 8, 11, 14, 17, __, __
b) 1, 5, 12, 22, 35, __, __
1 5 12 22 35
5 8 11 14 17
+3 +3 +3 +3 +4
Barisan Aritmatika Tingkat 1
+3 +3 +3
Barisan Aritmatika Tingkat 2
+13
+7 +10

4. MENENTUKAN RUMUS BARISAN ARITMATIKA BERTINGKAT
4
𝑎 + 𝑏
𝑎 𝑎 𝑎
Barisan Aritmatika Tingkat Satu:
𝑈𝑛 = 𝑎𝑛 + 𝑏
𝑈1 𝑈2 𝑈3 𝑈4
3 𝑎 + 𝑏 4𝑎 + 𝑏
2𝑎 + 𝑏

5. MENENTUKAN RUMUS BARISAN ARITMATIKA BERTINGKAT
5
𝑎 + 𝑏 + 𝑐
3𝑎 + 𝑏
𝑈1 𝑈2 𝑈3 𝑈4
Barisan Aritmatika Tingkat Dua:
𝑈𝑛 = 𝑎𝑛2 + 𝑏𝑛 + 𝑐
2𝑎 2𝑎
4𝑎 + 2𝑏 + 𝑐 9 𝑎 + 3𝑏 + 𝑐 16𝑎 + 4𝑏 + 𝑐
7𝑎 + 𝑏
5𝑎 + 𝑏

6. MENENTUKAN RUMUS BARISAN ARITMATIKA BERTINGKAT
6
Barisan Aritmatika Tingkat Tiga:
𝑈𝑛 = 𝑎𝑛3 + 𝑏𝑛2 + 𝑐𝑛 + 𝑑

7. Contoh Soal
7
4
𝑈1 𝑈2 𝑈3 𝑈4 𝑈5
Barisan Aritmatika
Tingkat Dua:
𝑼𝒏 = 𝒂𝒏𝟐
+ 𝒃𝒏 + 𝒄
3 3 3
Tentukan rumus suku ke-n dari barisan aritmatika bertingkat
1, 5, 12, 22, 35, …
1 5 12 22 35
7 10 13

8. Pembahasan Soal
8
Barisan Aritmatika Tingkat Dua: 𝑼𝒏 = 𝒂𝒏𝟐
+ 𝒃𝒏 + 𝒄
𝑎 + 𝑏 + 𝑐 = 1
Maka kita peroleh: 3𝑎 + 𝑏 =4
2𝑎 = 3

9. Pembahasan Soal
9
𝑎 + 𝑏 + 𝑐 = 1
Maka kita peroleh
rumus suku ke-n:
3𝑎 + 𝑏 =4
2𝑎 = 3 𝑎 =
3
2
𝑏 = 4 − 3
3
2
= −
1
2
𝑐 = 0
𝑼𝒏 = 𝒂𝒏𝟐
+ 𝒃𝒏 + 𝒄
𝑼𝒏 =
3
2
𝒏𝟐 −
1
2
𝒏

10. LATIHAN SOAL
10
Carilah rumus suku ke-n dari setiap barisan aritmatika
bertingkat berikut.
a) 6, 9, 16, 27, 42, 61, …
b) 5, 5, 11, 29, 65, 125, 215, …
c) 5, 13, 55, 179, 457, 985, 1883, …

11. Thank You