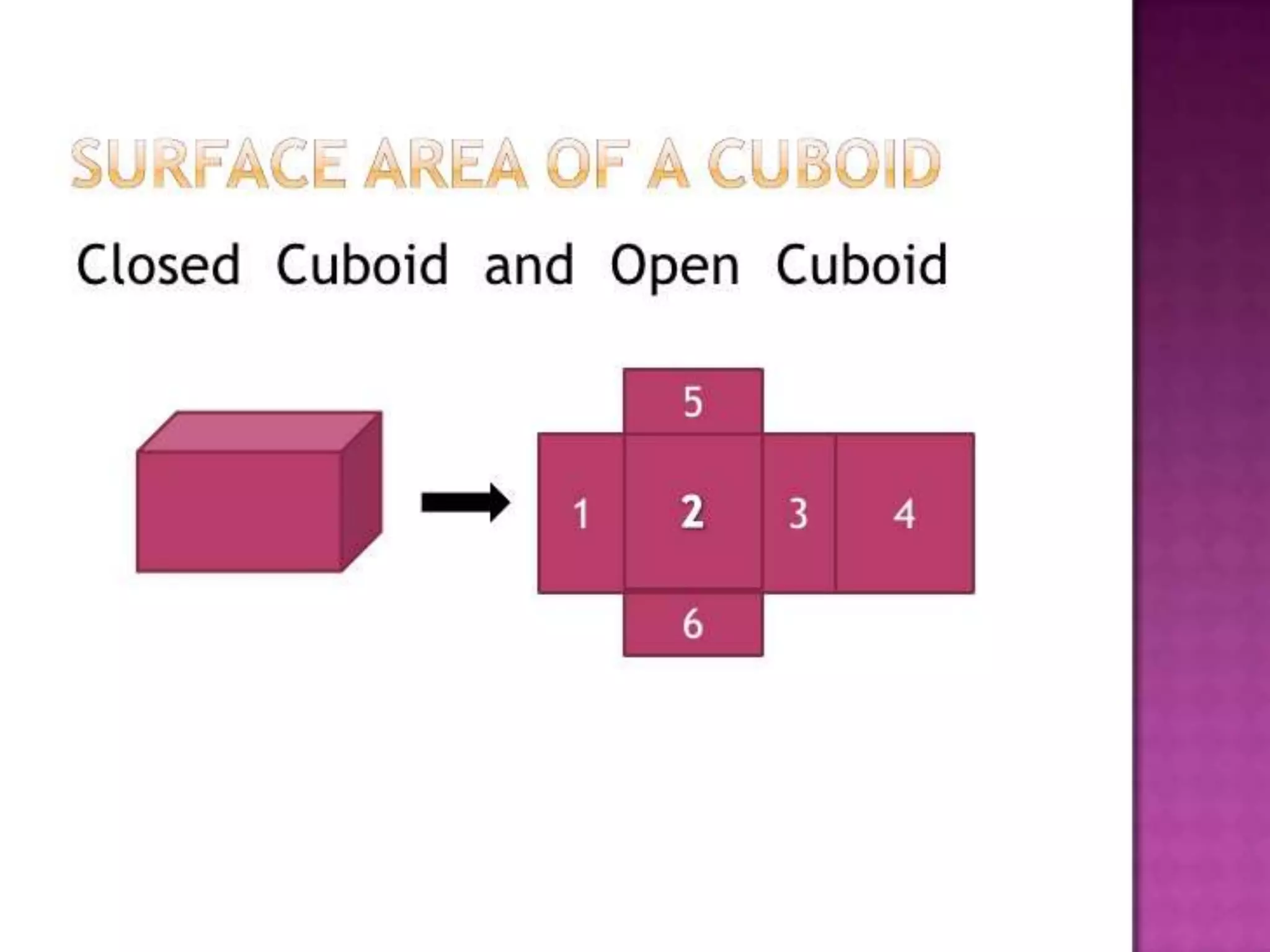
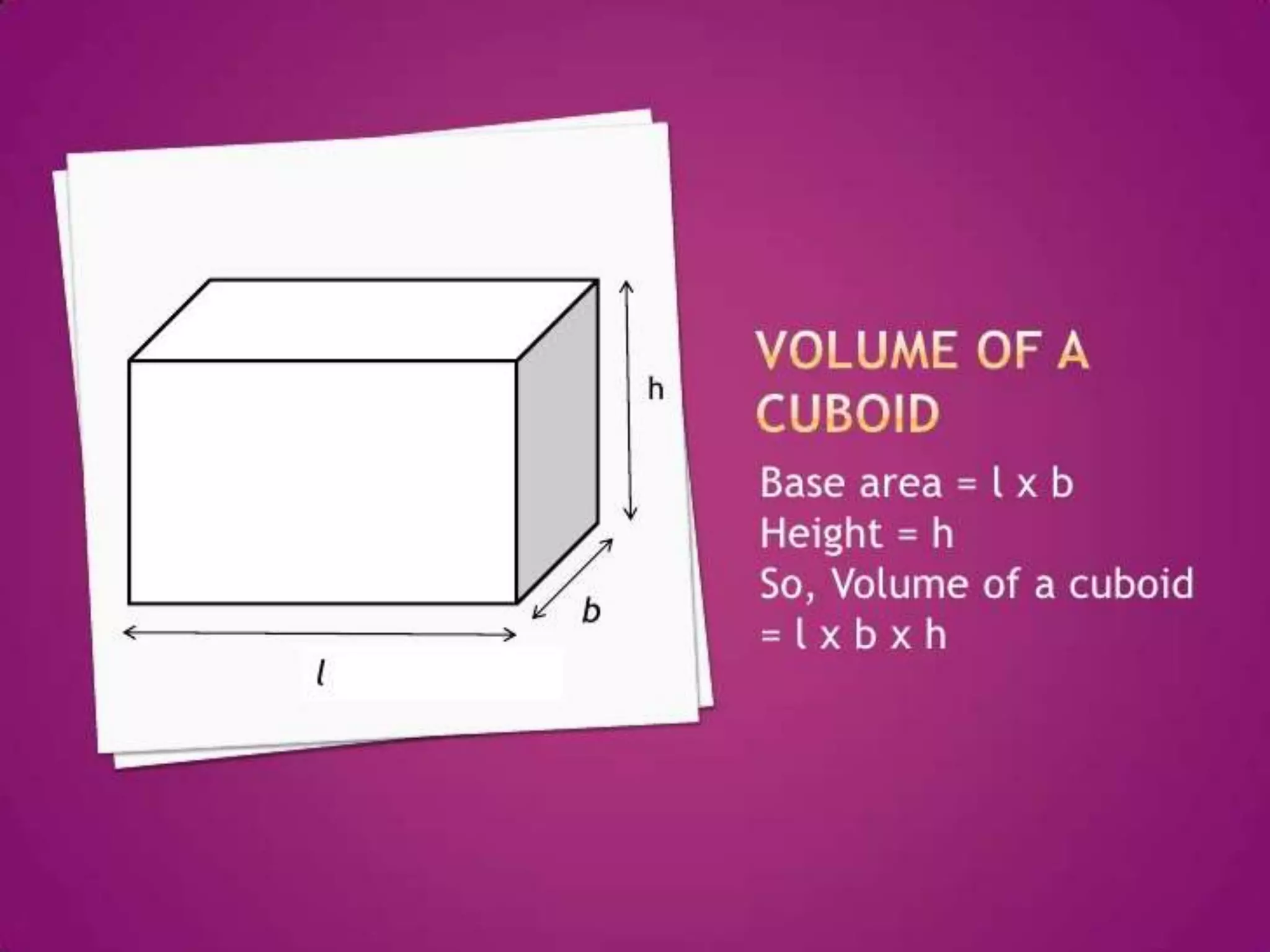
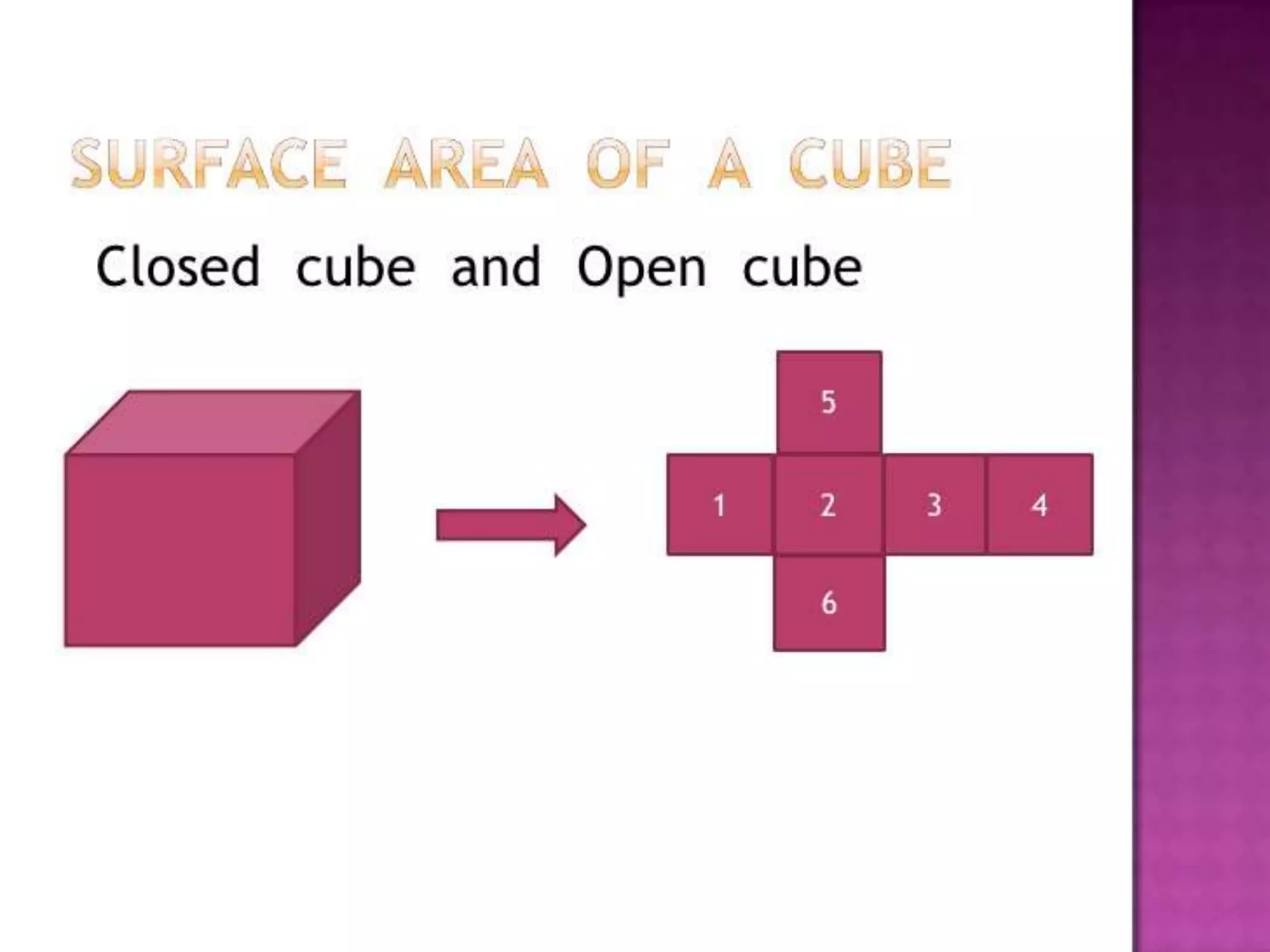
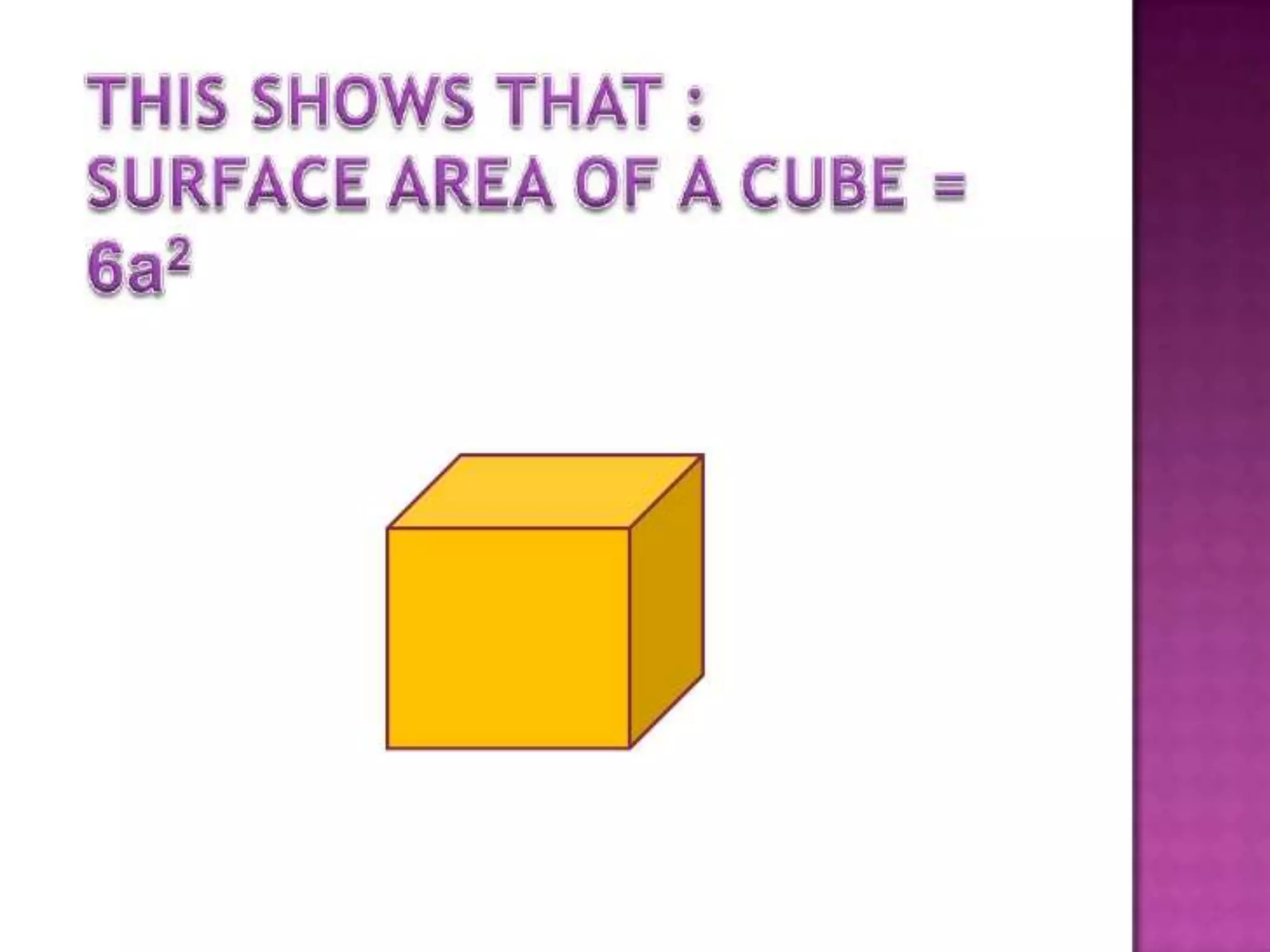
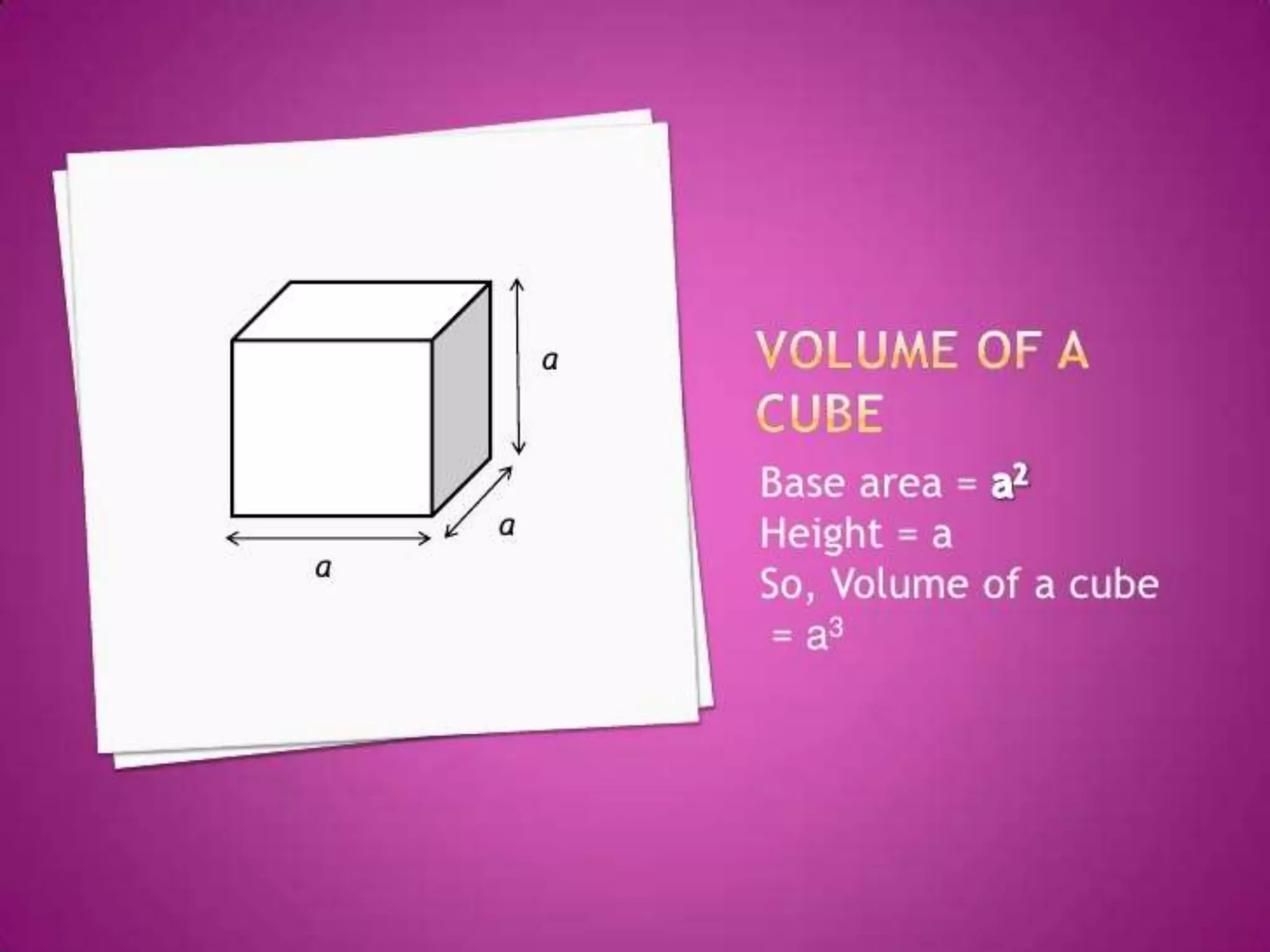
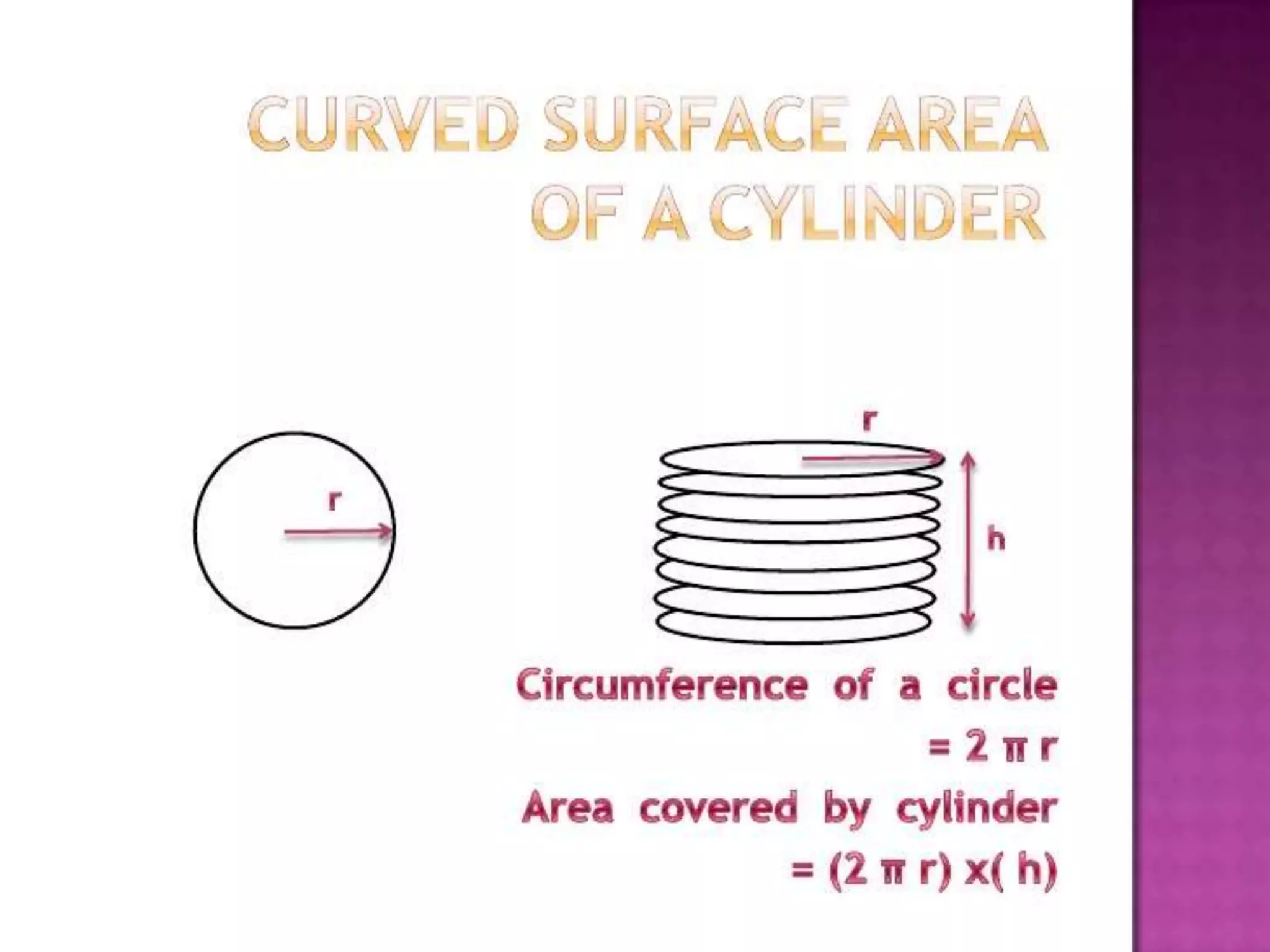
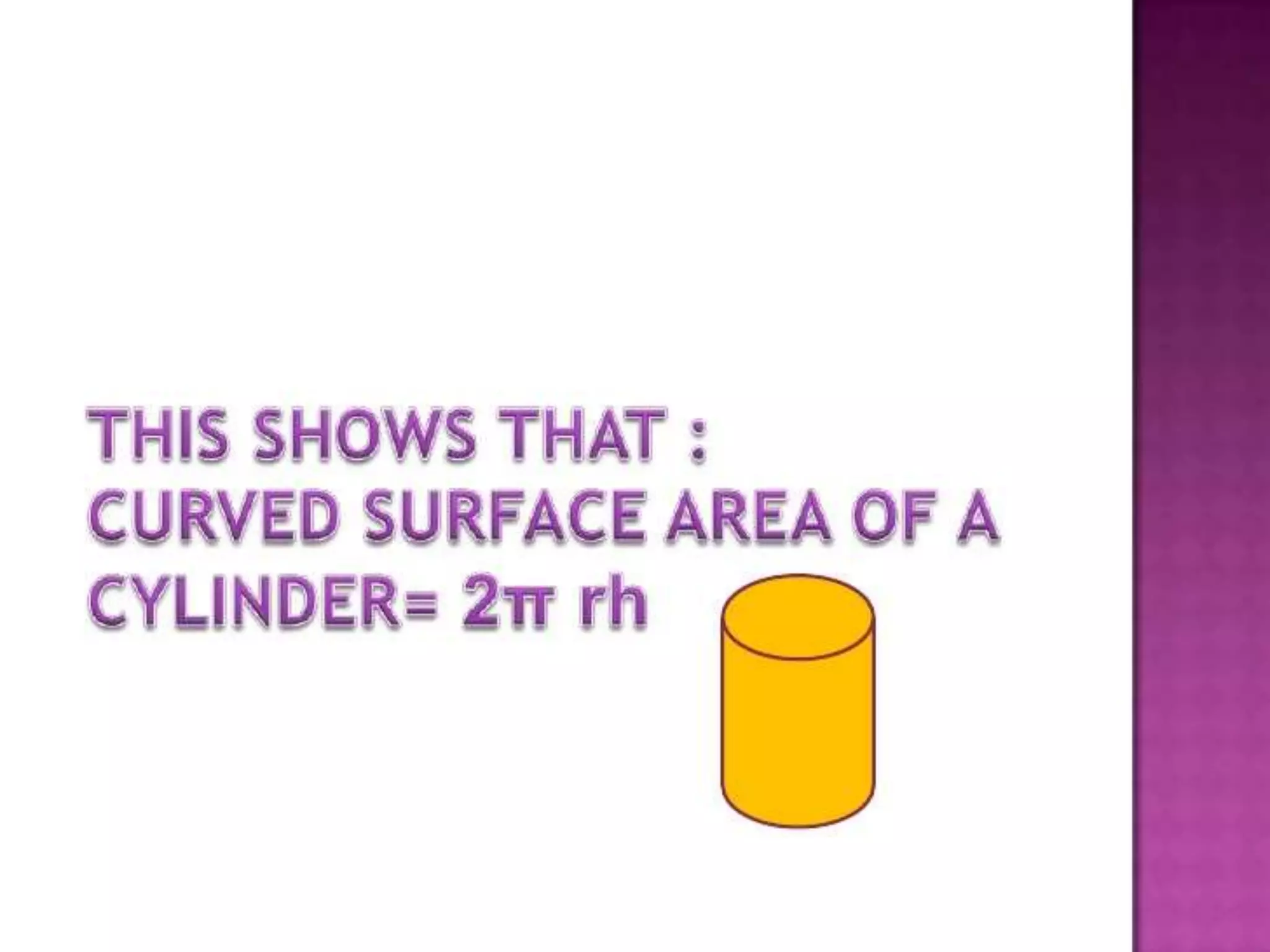
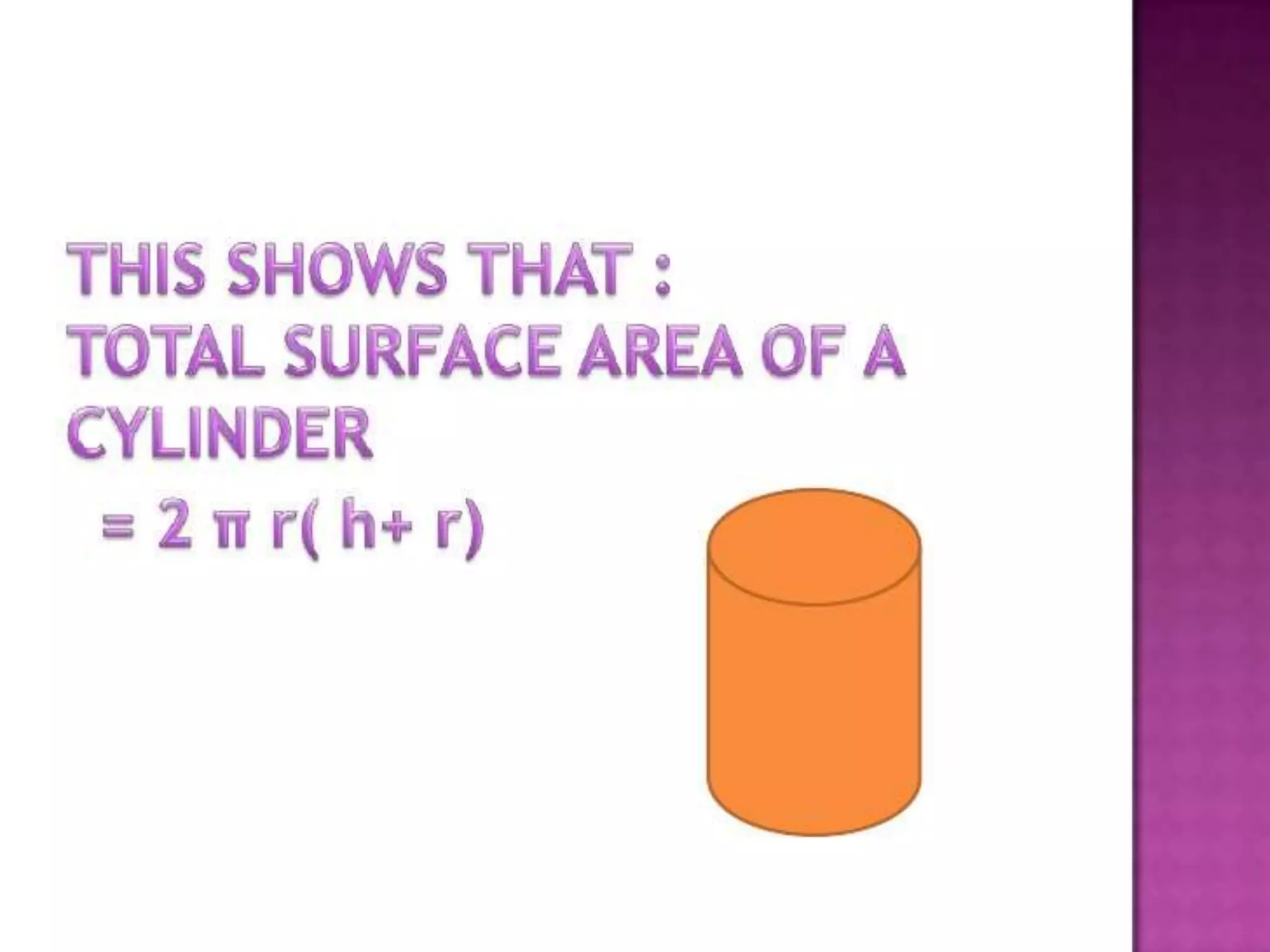
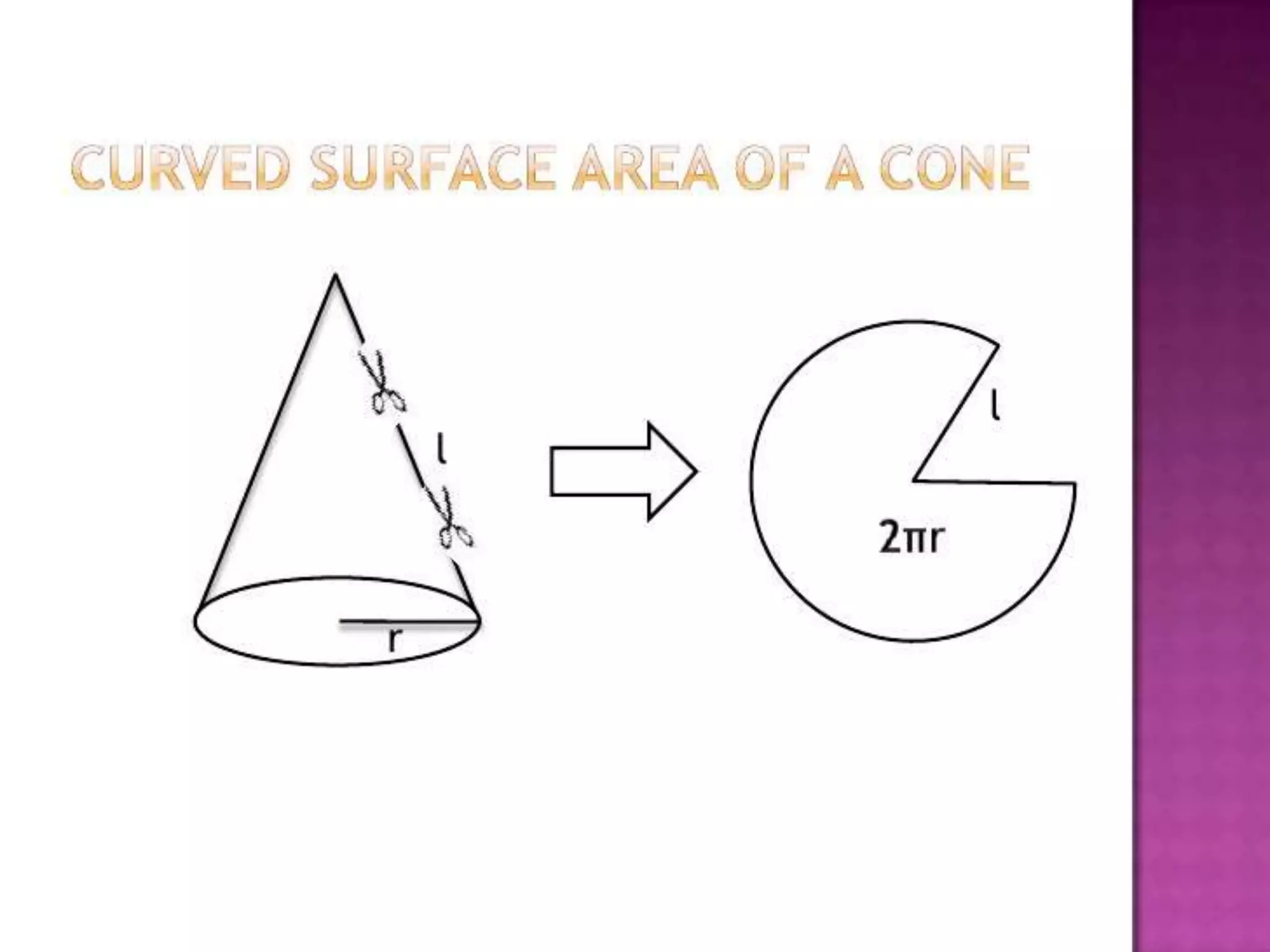
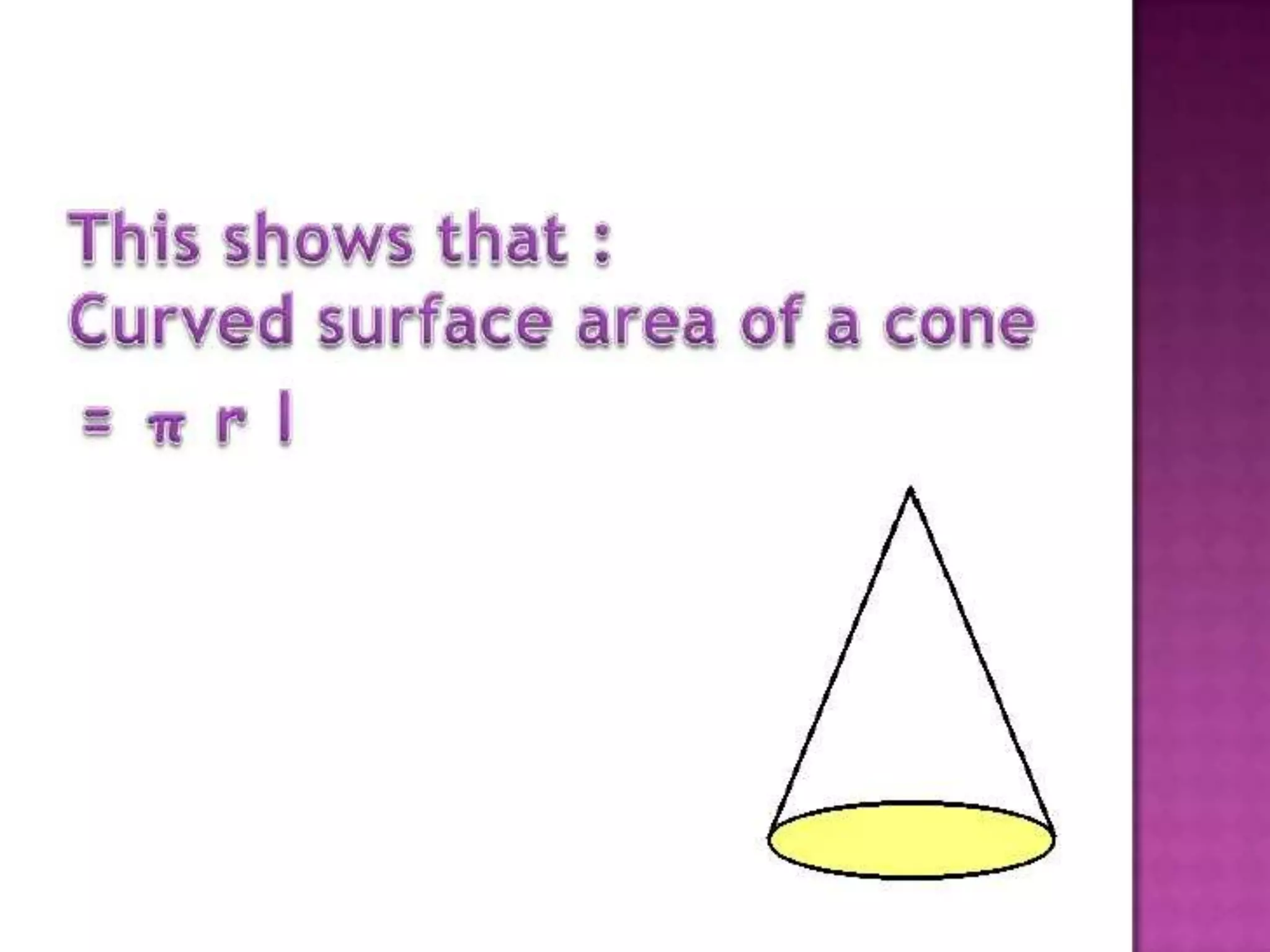
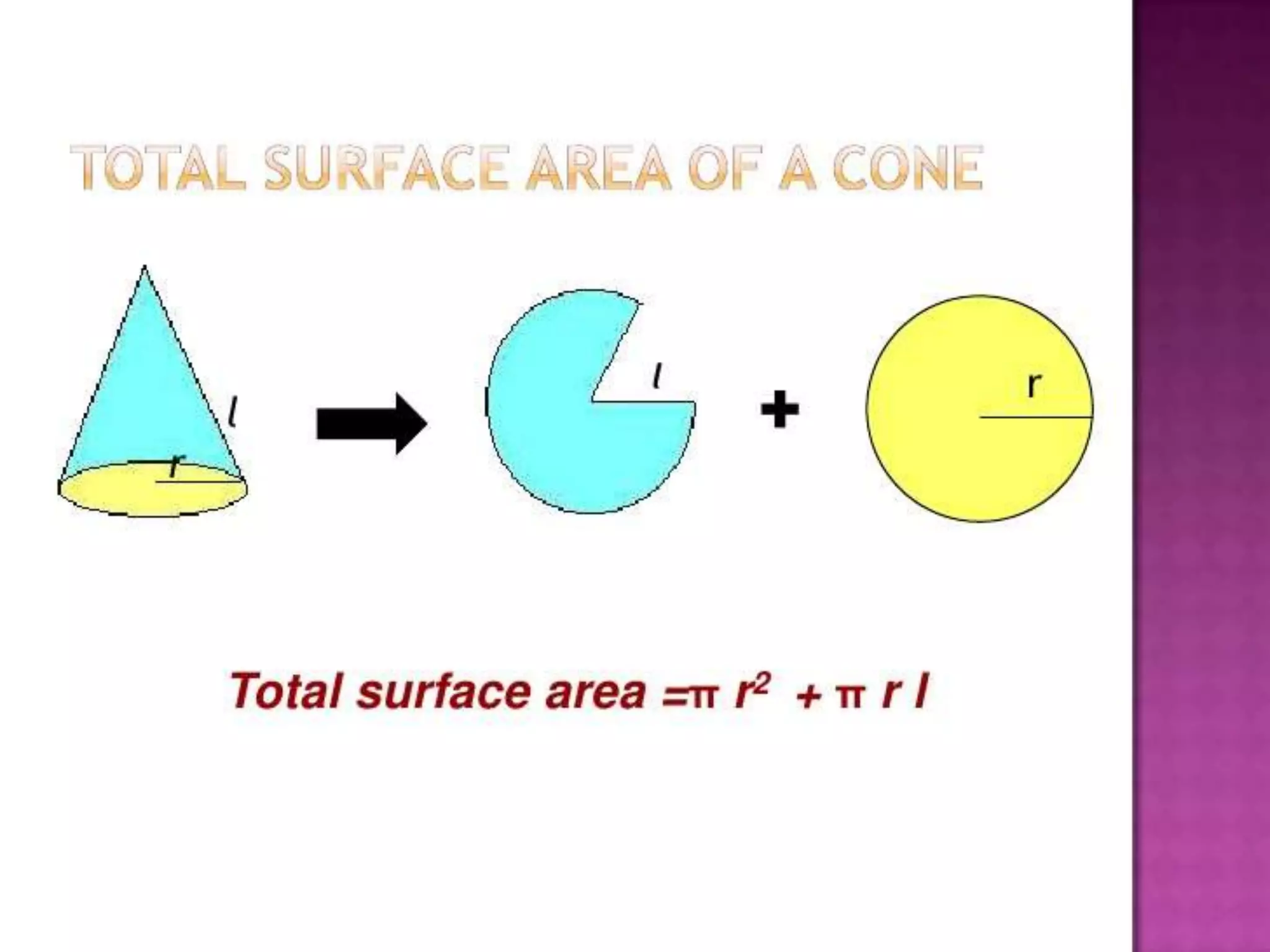
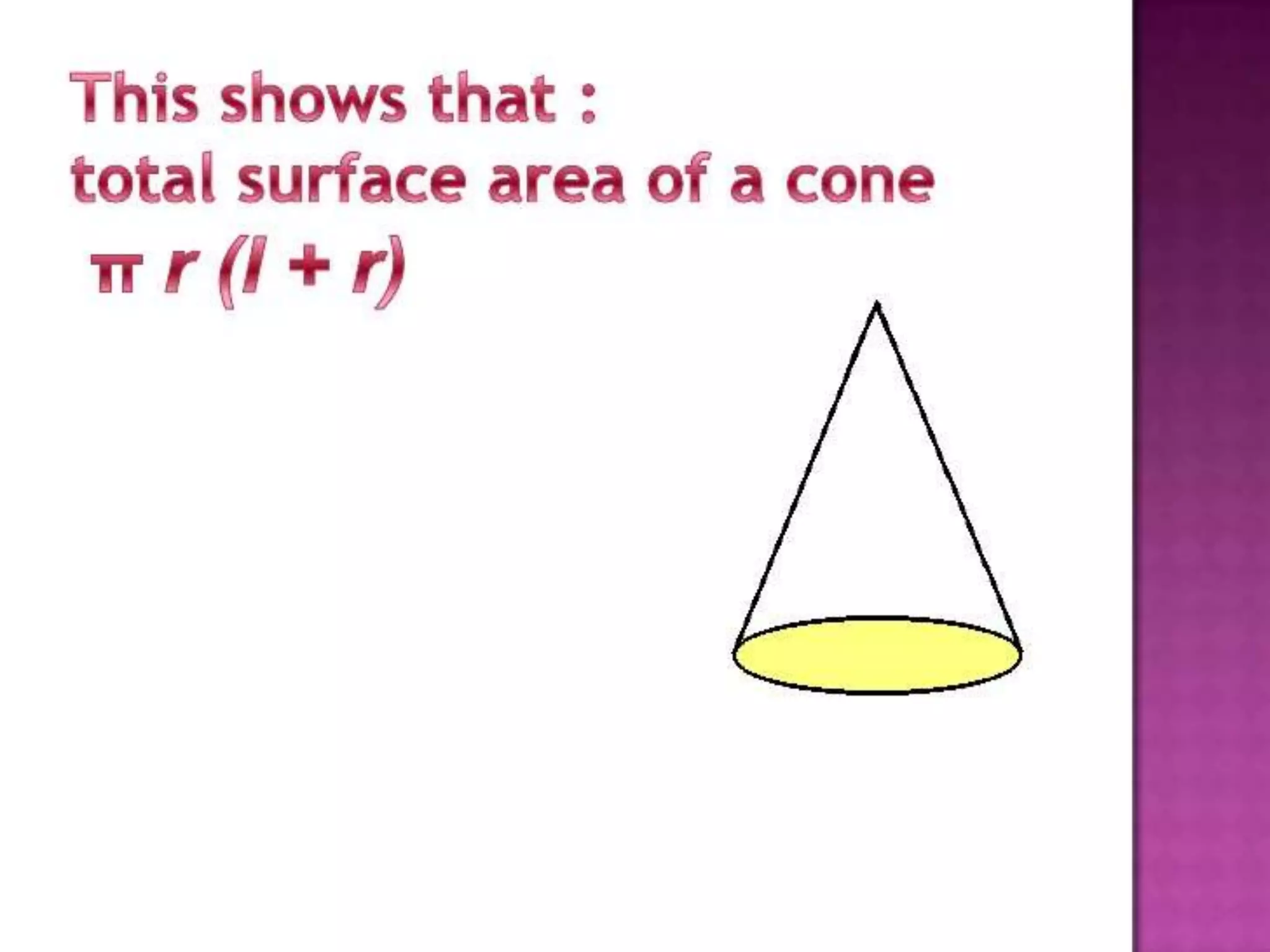
The document thanks the teacher, Mrs. Leena Saji, for giving the opportunity to do a presentation. It also thanks parents and friends for their help in finishing the presentation on time. Finally, it thanks God for everything and bringing the presentation to fruition.